GNSS海洋浮标海面高程动态不确定度研究

梁冠辉陶常飞*周兴华刘同木林冠英黄 桦

(1.自然资源部 第一海洋研究所,山东 青岛266061；2.自然资源部 南海局,广东 广州510301)

随着我国“十三五”海洋强国重大部署和“一带一路”的提出和推行,我国以及“一带一路”沿线各国在各自海域开展海洋经济和科研等活动会愈加频繁,海洋观测是各种海洋活动的前提[1-2]。为了丰富海洋观测手段和提高海洋观测效率,我们研制了基于GNSS(Global Navigation Satellite System)的海洋测量浮标并成功进行了海洋应用试验,GNSS海洋浮标的直接测量结果是瞬时海面高程,通过该结果可以开展海洋潮位、波浪等参数测量和星载卫星高度计在轨绝对定标等工作。为了使该浮标能够为实际海洋工作提供准确可靠的测量结果[3-5],根据海洋计量工作的要求[6-7],文中对该浮标测量结果开展了不确定度评定工作。

海洋现场测量与陆地或者实验室内测量相比具有不同的特征,测量过程中,该GNSS测量浮标在海面上随着海平面的起伏与波动时刻进行垂向运动和水平摇动；时刻变化的天气和海面状况会对浮标的姿态和浮标接收GNSS电磁波的质量产生动态随机的影响；浮标的测量结果潮位也是动态变化的。从计量角度来看,在GNSS浮标测量过程中,测量系统、测量环境和被测量均具有时变性、随机性和相关性等特点,因此该测量过程是一种动态测量[8-11]。

动态测量结果是一系列被测量瞬时值的集合,因此动态测量结果的不确定度同样是一系列被测量结果不确定度序列集合[12-13]。目前,针对动态测量不确定度评定的主要理论有灰色理论、贝叶斯理论和蒙特卡罗方法,这些方法在计算动态不确定度的方程各异方面,本质是一致的,将动态不确定度当作时间函数,运用相应的理论方法建立模型来评定[14-19]。GNSS测量浮标长时间自动在海洋中工作,复杂多变的测量环境和测量过程使其动态不确定度变化并不具备规律性,很难用某个模型来全面评定GNSS浮标测量结果的动态不确定度,而且不同的测量过程的不确定度也不能互相代替,必须针对每一个具体测量过程开展不确定度评定。文中根据GNSS浮标工作原理和数据处理方法,将浮标具体动态测量过程分解为一系列离散的静态测量过程,分析每个静态过程的不确定度分量,使用GB/T27418—2017《测量不确定度评定与表示》中GUM方法对每个静态测量过程进行不确定度评定[20],最终合成GNSS浮标瞬时海面高程的动态标准不确定度和动态扩展不确定度[21-24],以期为该浮标的使用者提供精准合格的测量结果,保证该浮标能够有效地服务于海洋观测工作。

1 GNSS测量浮标简介

GNSS浮标主要由GNSS天线、GNSS处理模块、姿态传感器、数据采集器、北斗通信终端、电源控制器、太阳能电池、蓄电池组和浮体组成,浮标原理图和实物如图1所示。

图1 GNSS浮标原理图和实物Fig.1 Schematic diagram and photo of GNSS buoy

GNSS天线实时接收GNSS卫星发射至地面的电磁波信号进行滤波放大等处理后,将其传输至GNSS处理模块,然后,GNSS处理模块对卫星信号进行A/D转换和数字信号处理后通过电文解析和定位解算得到浮标水平坐标、GNSS天线高程和时间等观测量。姿态传感器实时测量浮标的横滚角和俯仰角,用于后处理改正浮标的GNSS天线高程。

海洋现场测量工作完成后,首先提取浮标观测的GNSS数据和姿态数据,并将GNSS数据利用差分后处理算法解算得到浮标GNSS天线相位中心大地高程序列,然后利用姿态数据对浮标GNSS天线相位中心大地高程序列进行天线高程改正得到浮标所测海域的瞬时海面大地高程序列,对这些瞬时海面高程序列进行高程异常改正求得被测海域瞬时海面正常高程序列[25]。

2 不确定度评定

2.1 测量模型

根据GNSS浮标的观测原理,瞬时海面高程测量结果的计算公式：

式中,i为观测序号,i=0,1,2,…,n；Hi为瞬时海面高程；H0i为浮标经过差分解算后测得GNSS天线相位中心处大地高；hi为观测站的GNSS天线高程改正,即GNSS天线相位中心至浮标吃水面距离；N为浮标测量海域的高程异常值,该值由模型算法求得,在固定海域为固定值。

式(1)中Hi的3个输入量互不相关,所以Hi的动态合成标准不确定度计算公式为

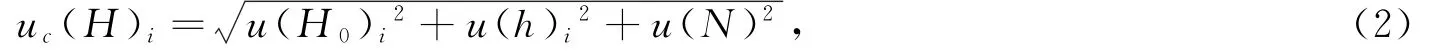
分别评定u(H0)i,u(h)i和u(N),然后合成uc(H)i。

2.2 瞬时海面高程动态不确定度评定

标准不确定度分量评定方法有2种：1)根据一系列测得值采用统计方法获得实验标准差的方法为A类评定；2)根据有关信息估计的先验概率分布获得的标准偏差估计值的方法为B类评定。其中A类评定方法要求进行多次独立重复测量,该过程中需具备重复性或者可复现的测量条件,若无法对被测量进行多次重复测量,则不确定度评定时无法进行A类评定,而可以进行B类评定。文中以GNSS浮标测量原理为基础,具体分析GNSS浮标海洋测量过程,选择合适的方法对每个不确定度分量进行评定。

2.2.1 GNSS高程动态标准不确定度u(H0)i

GNSS高程是GNSS天线相位中心大地高程,是通过载波相位差分后处理算法求得。由于测量过程及被测量的动态性,无法进行独立重复测量来通过统计方法获得GNSS高程的标准差,因此文中不对其进行A类不确定度评定,而是通过B类方法评定其标准不确定度。GNSS高程结果中包含高程及高程RMS值等信息,RMS值是GNSS数据处理过程中由验后残差计算所得,可用来表征其测量精度[26-28],采用GNSS高程解算结果中的RMS值的绝对值作为被测量可能值区间的半宽度,且GNSS高程动态标准不确定度服从均匀分布,包含因子为,则动态测量中,GNSS高程测量动态标准不确定度u(H0)i的计算公式为

式中,Ri为动态测量中GNSS高程测量结果可能值区间的半宽度。

2.2.2 GNSS天线高程改正动态标准不确定度u(h)i

GNSS天线高程改正是指GNSS天线相位中心至海面的动态高度,本文中研制的GNSS浮标天线安装在浮标纵向中心轴,改正公式为

式中,hi为GNSS天线相位中心至海面的动态垂向距离；h0为静水时GNSS天线相位中心至海面的垂向距离,对于同一个浮标,该值为固定值；εi和θi分别为GNSS浮标动态横滚角度和俯仰角度。

从式(4)中可以看出,GNSS天线高改正的不确定度输入量有3个,其中h0采用全站仪测得,εi和θi通过浮标内置姿态测量传感器测得,因此h0与εi和θi不相关,相关系数为0,εi和θi的相关系数通过实测数据计算所得。

按照不确定度传播律,GNSS天线瞬时高程改正动态标准不确定度u(h)i合成公式：

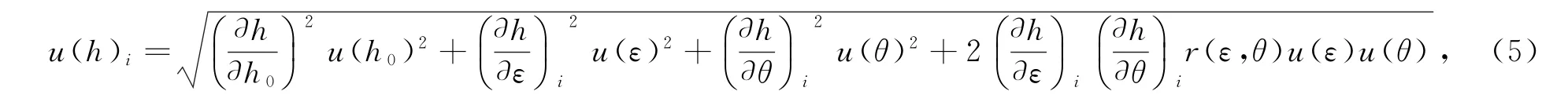
式中,u(h0),u(ε)和u(θ)分别为h0,ε和θ的标准不确定度,为h0的灵敏系数为动态横滚角灵敏系数,计算公式为

εi和θi的计量特征与浮标测得的GNSS高程相似,需通过B类方法评定二者的标准不确定度,将姿态测量传感器说明书中二者的最大允许误差绝对值作为二者测量值可能值区间的半宽度aε和aθ,服从均匀分布,包含因子kε和kθ均为,则εi和θi的不确定度计算公式为

通过全站仪测量所得h0的标准不确定度主要来源有外界气象条件(如气温、气压等)和全站仪自身的原因(如棱镜常数、轴系误差等),经过评定u(h0)为毫米量级,GNSS天线高程改正的总体不确定度为厘米量级,u(h0)远小于u(h)i,在计算过程中可以忽略不计,GNSS天线高程改正动态标准不确定度u(h)i计算公式可简化为

2.2.3 高程异常不确定度u(N)

文中高程异常值是利用最新的全球大地水准面模型EGM 2008结合区域GPS或水准网点成果精化区域大地水准面模型计算所得。该值取决于所在区域的模型精度,若所在区域实测数据较多,模型同化效果较好,则模型精度较高,因此高程异常不确定度评定需根据浮标所在区域开展具体的评定工作。根据研究人员在浮标所在区域的大地水准面测量工作经验来确定高程异常值的最大允许误差aN,该值服从均匀分布,取包含因子为,则高程异常标准不确定度计算公式[29-30]：

2.2.4 瞬时海面高程动态合成标准不确定度uc(H)i和瞬时海面高程动态扩展不确定度U99i

瞬时海面高程动态合成标准不确定度uc(H)i由式(3),式(10)和式(11)求得的不确定度分量u(H0)i,u(h)i和u(N)代入式(2)中合成所得。

假设瞬时海面高程动态合成标准不确定度服从均匀分布,取包含概率p=0.99,包含因子kp=1.71,则瞬时海面高程动态扩展不确定度计算公式：

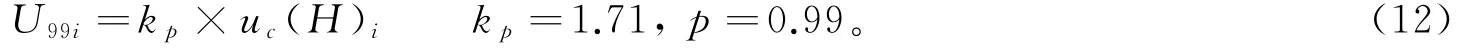
3 试验分析

以2018-09-19在自然资源部南海局广州长洲岛码头使用GNSS浮标开展试验为例,按照上述步骤构建的不确定度评定模型对试验结果开展不确定度评定,试验中GNSS浮标观测数据采样频率为1 Hz。首先提取浮标的GNSS解算结果中的Ri与经过式(3)计算的u(H0)i如图2所示。

GNSS高程动态标准不确定度曲线取决于GNSS高程结果的RMS值曲线。GNSS高程RMS值作为评价GNSS高程精度的主要指标之一,主要反映了高程观测质量的优劣,即高程观测值与参数估计值之间的符合程度,该值越小,说明高程观测值质量越好。它与GNSS原始观测量中的多路径效应、电离层对相位的影响、电离层延迟的变化及接收机的钟漂和周跳等因素有密切关系,这些因素有的受外界环境影响,有的受观测仪器本身的影响。但是,在GNSS数据处理过程中,差分后处理算法会对这些影响因素进行消除或者抑制,最终得到GNSS高程RMS序列代表GNSS整个观测过程的最终结果精度,这个过程包括GNSS卫星信号传播、GNSS卫星信号接收和GNSS数据处理等步骤。外界环境复杂而随机,导致RMS值的变化亦随机无规律,但数据处理过程的优化使RMS值的变化具有一定的平缓性。所以每一次具体的GNSS测量过程的RMS值曲线都不相同。

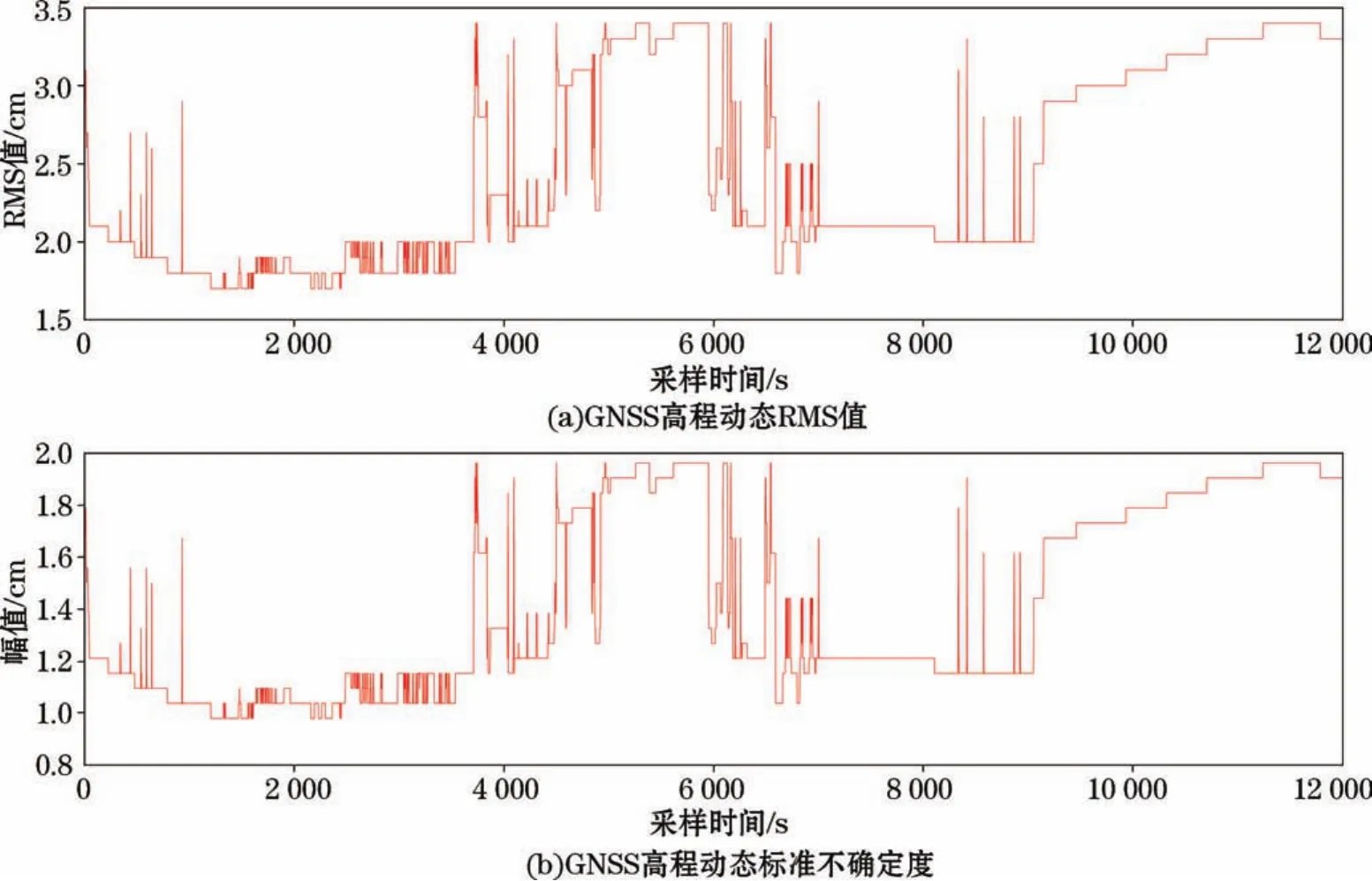
图2 浮标GNSS动态高程RMS值和高程动态标准不确定度Fig.2 RMS value and uncertainty of dynamic elevation measured by GNSS buoy

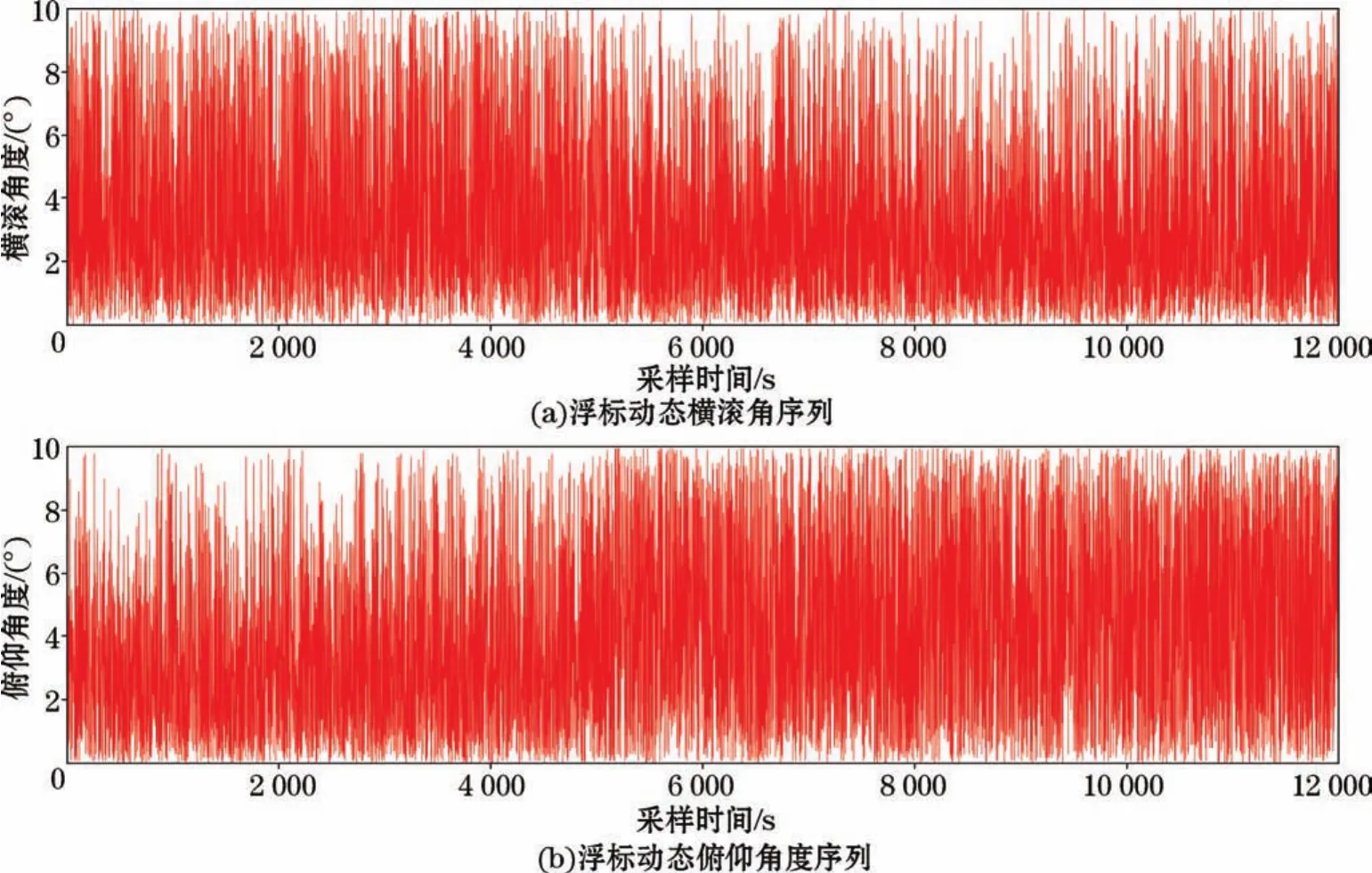
图3 浮标动态横滚角度和俯仰角度Fig.3 Dynamic roll angle and pitch angle of the buoy

GNSS浮标横滚角和俯仰角测量结果如图3所示,横滚角和俯仰角反应了浮标工作时所在海域的随浪性,由于浮标体的对称性,二者的幅值特征主要取决于浮标数据采样时所在海域的波浪的波向和浪高；频率特征由浮标本身固有的摇荡周期和波浪周期决定。我国近海的波浪周期一般为6～8 s,而GNSS浮标的横摇固有周期约为10 s,所以图3中浮标的横摇角和俯仰角的变化频率要远高于浮标GNSS高程RMS值的变化频率。

研制浮标时测量得到的静水时GNSS天线相位中心至海面的垂向距离h0=143.6 cm。通过图3中横滚角和俯仰角序列计算二者相关系数r(ε,θ)=0.011,查阅姿态测量传感器说明书中二者的最大允许误差绝对值均为0.2°,则aε=aθ=0.2°。将数据分别代入式(6)～式(10),计算出u(h)i(图4)。

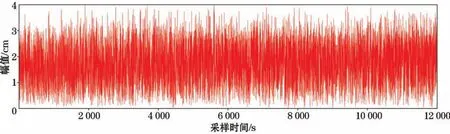
图4 GNSS天线高改正动态标准不确定度Fig.4 Dynamic uncertainty of the GNSS antenna height correction

根据此次试验浮标所在区域的其他的工作经验,利用EGM 2008模型计算高程异常不确定度的最大允值误差,得aN=±5 cm,代入式(11)求得高程异常不确定度。将瞬时海面高程动态标准不确定度的3个分量代入式(2)计算得uc(H)i(图5a)。最终,通过式(12)合成瞬时海面高程动态扩展不确定度,如图5b所示。

图5中的动态合成标准不确定度和动态扩展不确定度为此次不确定度评定的最终结果,高程异常标准不确定度为常量,它们的曲线特性主要受GNSS高程动态标准不确定度和GNSS天线高改正动态标准不确定度影响。图中既体现出GNSS高程动态标准不确定度变化的趋势,也包含了GNSS天线高改正动态标准不确定度的幅频特征。

图5 瞬时海面高程动态合成标准不确定度和瞬时海面高程动态扩展不确定度Fig.5 Dynamic synthesis standard uncertainty and dynamic expanded uncertainty of the instantaneous sea-level elevation

4 结 语

综合考虑GNSS测量浮标的工作原理、系统组成、数据处理方法和测量环境等因素,针对浮标具体的动态测量过程提出了一种GNSS测量浮标不确定度评定方法。该方法对动态测量的每一个结果均提供不确定度,可以详细判断整个测量过程中每个数据的质量,保证该GNSS浮标测量的瞬时海面高程能准确地应用于海洋科学研究和工程开发等工作中。

不确定度评定过程中,分析和计算了3个动态不确定度分量,由此可知影响瞬时海面高程动态合成标准不确定的主要因素有：传感器的测量指标、浮标所处的海洋环境和高程异常计算模型的精准度。这对GNSS测量浮标的使用场合的选择和研制的优化均有指导作用。