高超声速飞行器预警资源分配方法
罗 艺,谭贤四,王 红,曲智国,李同晓,封兴凯
(1.空军预警学院 三系, 武汉 430019;2.中国人民解放军94326部队,济南 250023;3.华中师范大学 心理学院,武汉 430079;4.中国人民解放军95662部队,林芝 540401)
高超声速飞行器,具有升力式气动布局,可进行高速、长距离、无动力滑翔飞行[1-3]。这种飞行器在气动外形、运行环境、飞行受力、控制方式和机动模式等方面与弹道导弹存在明显差异,其跳跃滑翔运动过程中难以观测和跟踪,给预警探测系统带来了极大的挑战[4]。因此,需要一种有效的资源分配方法,该方法能够针对目标的运动特性进行资源分配。
资源分配理论在各种领域都有非常重要的应用价值,对于这方面的研究也取得了一些成果[5-6]。预警资源分配的方法可以分为2种:一种是基于信息指标优化的方法[7];另一种是基于决策过程优化的方法[8-9]。第1种方法将信息评价指标作为目标函数对传感器进行资源分配,来提高跟踪精度;第2种方法将控制策略、回报函数或风险函数作为目标函数来进行资源分配。这些方法提供了理论基础,对于高超声速目标的预警资源分配还需要针对高超声速飞行器的运动特性进行研究。
针对以上问题,本文提出了高超声速飞行器跳跃滑翔运动过程中的预警资源分配方法。首先根据高超声速飞行器跳跃滑翔的运动特性,建立了马尔可夫运动状态转移模型,该模型能够有效的反映出高超声速飞行器运动状态的变化,为预警资源分配提供了基础。结合目标的马尔可夫模型,基于隐马尔可夫模型(Hidden Markov Model,HMM)理论[10]提出了预警资源的分配方法,该方法将先验信息和观测值相结合,为资源分配决策提供了依据。资源分配过程中将单位资源消耗产生的信息增量最大化作为目标函数,保证了预警过程中对目标的跟踪精度。最后,通过仿真实验验证了该方法能够对预警资源进行合理分配。
1 马尔可夫状态转移模型
高超声速飞行器具有高升阻比的气动布局,当其重新进入大气层后,在气动升力的托举下可以跳跃滑翔飞行,因此高超声速飞行器的运动特性与常规目标存在显著差异。
尽管高超声速飞行器具有高机动的运动特性,如图1所示,但是其跳跃滑翔运动阶段的轨迹存在近似的解析关系,因此可以根据弹道方程进行状态估计,如式(1)所示:
(1)
式(1)中:h为飞行高度;R为地球半径;V飞行器速度;γ为当地速度倾角;D为阻力;L为升力;M为飞行器质量;χ为经度;φ为纬度;ψ为航向角;σ为倾侧角,该运动方程为速度坐标系下的飞行器运动方程。
高超声速飞行器在滑翔运动过程中可以分为5种状态,如图1所示。这5种状态是再入机动状态、下降状态、跳跃机动状态、上升状态和攻击状态。
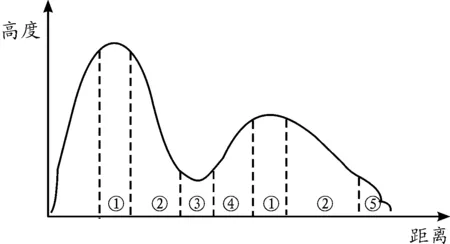
图1 高超声速飞行器跳跃滑翔运动轨迹
定义高超声速飞行器跳跃滑翔运动过程为连续时间的马尔可夫过程{X(t),t≥0},如图2所示,其状态空间S={sn|n=1,2,3,4,5},对任意0≤t1≤t2≤…tk+1及s1,s2,…,sn∈S,有
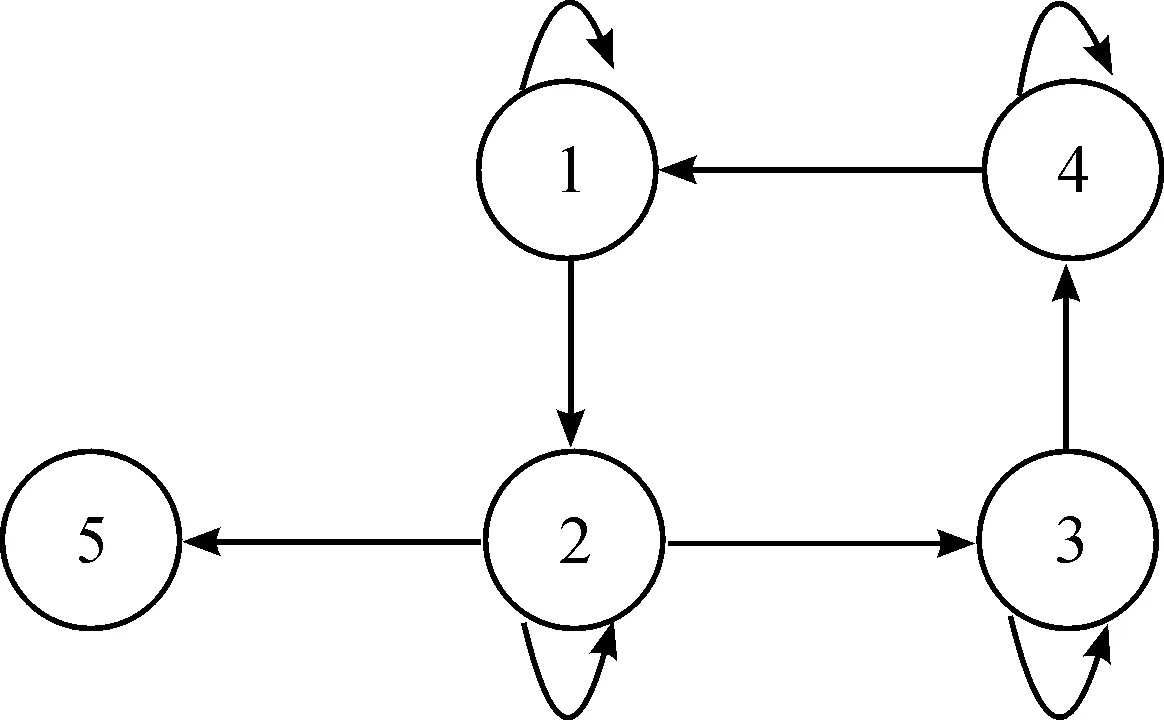
图2 高超声速飞行器跳跃滑翔运动的马尔可夫运动模型
P{X(tk+1)=sn+1|X(t1)=s1,X(t2)=s2,…,X(tk)=sn}=
P{X(tk+1)=sn+1|X(tk)=sn}
(2)
2 基于HMM的资源分配方法
2.1 资源分配模型
假设对高超声速飞行器的预警探测时刻为k∈{1,2,…,K},k时刻高超声速飞行器的状态转移概率矩阵为
A(k)=[aij(k)]={P(x(k)=sj|x(k-1)=si)}
(3)
式中,x(k)∈{si|i=1,2,…,5},表示HMM在k时刻的隐状态;si为高超声速飞行器的运动状态。
k时刻高超声速飞行器的观测概率矩阵为
Y(k)={P(y(k)=so|x(k)=si)}
(4)
式中,y(k)为高超声速飞行器的观测状态。
若初始状态的概率分布为π,则隐马尔可夫模型如图3所示,可表示为

图3 隐马尔可夫模型框图
λ(k)=(A(k),Y(k),π),k=1,2,…,K
(5)
假设k时刻可用的预警资源为ω(k)⊆{1,2,…,m},m为预警资源的数量,对目标(即高超声速飞行器)进行观察的资源为w(k),w(k)∈ω(k),基于HMM预警资源的分配模型如图4所示。
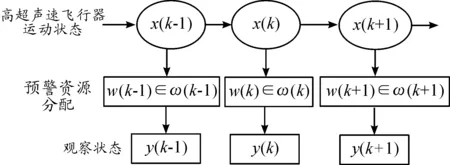
图4 资源分配模型框图
则在k时刻,观测概率矩阵为 可表示为
Y(k)={P(y(k)=so|x(k)=si,w(k)=q)}
(6)
HMM所具有的信息集合为{Yk-1,Wk-1},其中
Yk-1={y(1),y(2),…,y(k-1)}
Wk-1={w(1),w(2),…,w(k-1)}
(7)
Yk-1表示k时刻之前的观察值的序列,Wk-1表示k时刻之前分配预警资源的序列。在信息集合{Yk-1,Wk-1}的基础上对隐状态x(k)的预测概率可表示为
π(k|k-1)=P(x(k)|Yk-1,Wk-1)
(8)
2.2 目标函数
为了解决高超声速飞行器预警过程中的观测不确定问题,资源分配要以获得信息最大化为目标。这里引入信息熵的概念作为衡量信息的指标。
信息熵的计算公式为
H(X)=-∑P(xi)log(P(xi))
(9)
由式(9)可得对目标隐状态预测的信息熵为

(10)
预警资源分配的信息熵为
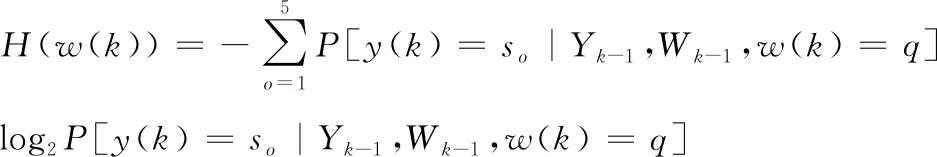
(11)
由条件熵的计算公式
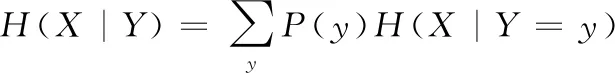
(12)
可得
H(w(k)|π(k|k-1))=
(13)
为了表示预警资源分配后对高超声速目标观察信息量的变化,本文使用信息增益来表示。信息增益指,知道某一信息后对另一信息不确定的减少量.这里信息增益可表示为
I(π(k|k-1),w(k))=H(w(k))-
H(w(k)|π(k|k-1))
(14)
由式(14)可得预警资源消耗所带来的信息增益的变化可表示为
(15)
式中c(w(k),π(k|k-1))为预警资源的损耗总成本。
预警资源的使用总成本可表示为
c(w(k),π(k|k-1))=
c1(w(k),π(k|k-1))+c2(w(k))
(16)
式中,c1(w(k),π(k|k-1))为预警资源的使用损耗成本;c2(w(k))为预警资源的切换损耗成本。
由此可得高超声速飞行器预警资源分配的目标函数为

(17)
式中的约束条件为:必须分配预警资源给目标,预警资源的分配不能为空集;目标位置必须在所分配的预警资源的威力范围中。根据对目标不同的预警任务,约束条件可以进行调整。
2.3 资源分配步骤
高超声速飞行器预警资源分配过程如图5所示,具体步骤如下:

图5 资源分配过程框图
步骤1:状态初始化。设置分配模型的初始状态以及初始状态概率。
步骤2:预测信息状态。根据上一时刻的信息状态π(k-1|k-1),计算出当前时刻的信息状态π(k|k-1)。
当前时刻信息状态的计算公式为
π(k|k-1)=A(k)π(k-1|k-1)
(18)
步骤3:计算信息增益。由于给每个预警资源获得的信息增益是不同的,根据式(14)计算出各资源的信息增益。
步骤4:分配资源。求解出满足目标函数式(17)最大的资源分配方案进行预警资源分配w(k)。
步骤5:得到当前时刻观测值。根据上一步得到的分配方案,对目标进行观测,并更新观测序列Yk={y(1),y(2),…,y(k-1),y(k)}。
步骤6:更新状态。根据当前时刻的信息集合{Yk-1,Wk-1}和π(k|k-1)计算出当前时刻的信息状态π(k|k)=Y(k-1)π(k|k-1),为下一时刻的状态预测做准备。
步骤7:返回步骤2,进入下一时刻的资源分配。
3 仿真分析
本节进行仿真实验,设定仿真场景如下:某时刻,高超声速飞行器以10Ma的速度向我方袭来,其运动轨迹如图6所示,飞入我方领空后预警资源的部署如图7所示。图7中1为预警机,正在进行8字巡逻,2为艇载雷达部署在空中,3和4为地基雷达。

图6 高超声速飞行器运动轨迹
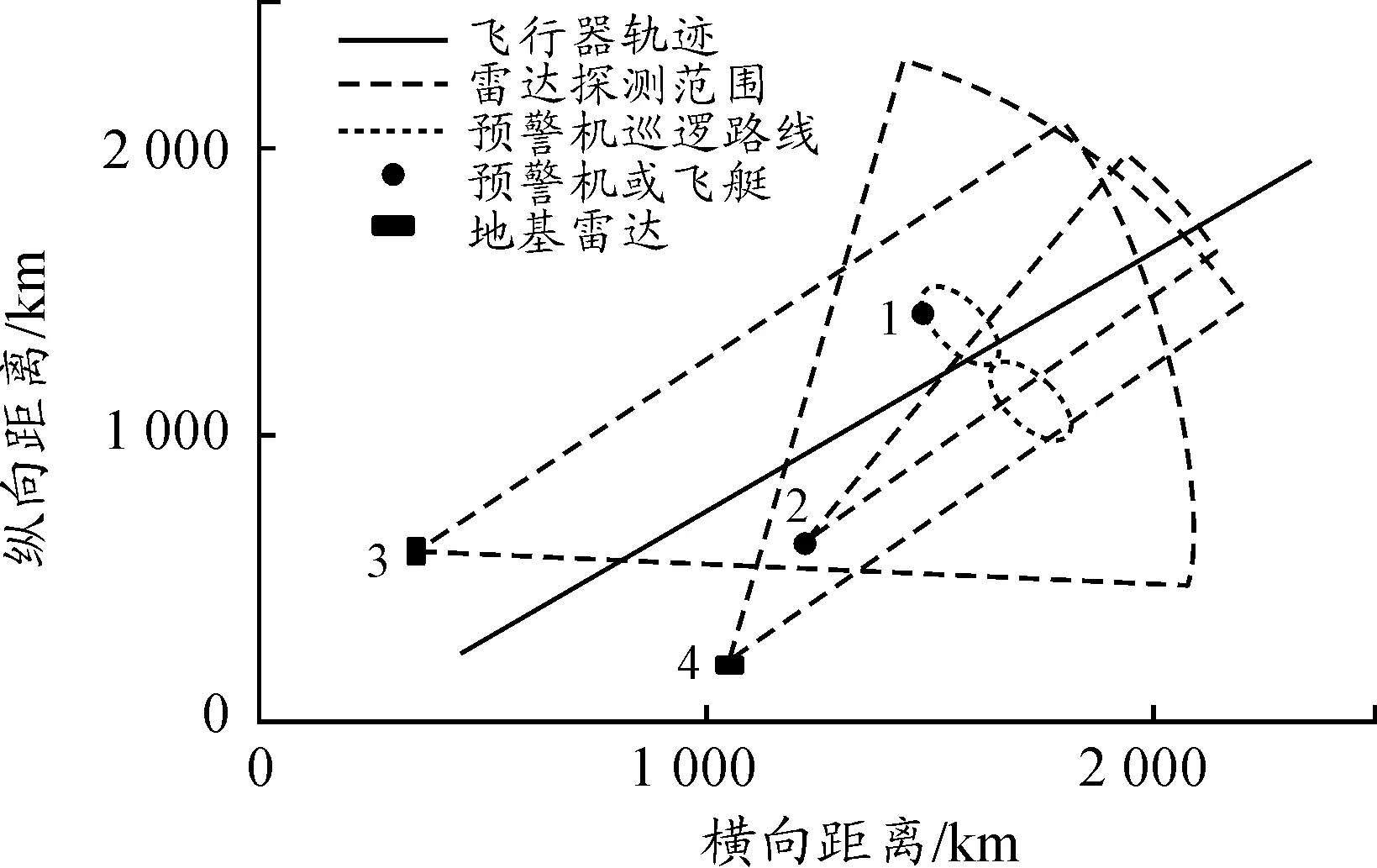
图7 预警资源部署仿真场景示意图
预警资源参数如表1所示。
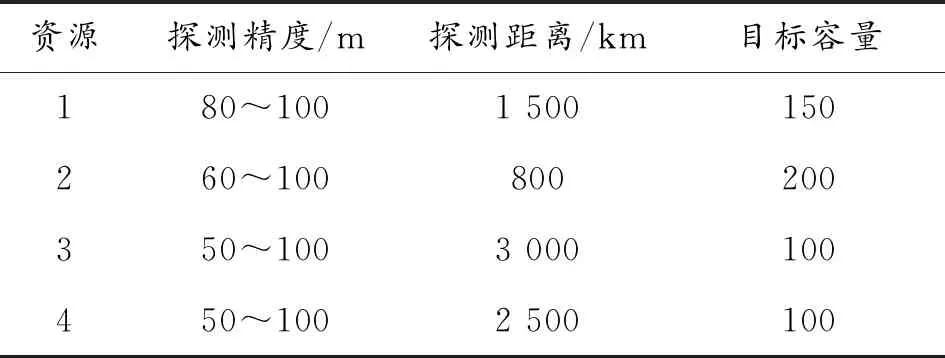
表1 预警资源参数
本实验使用Matlab软件进行仿真。实验分为两组:一组通过本文所提出的资源分配方法进行仿真;另一组在未使用资源分配的方法下将所有雷达的观测数据进行数据融合。两组实验对资源的使用、单位资源损耗下的信息增益以及跟踪结果的精度进行对比。实验结果如图8~图10所示。
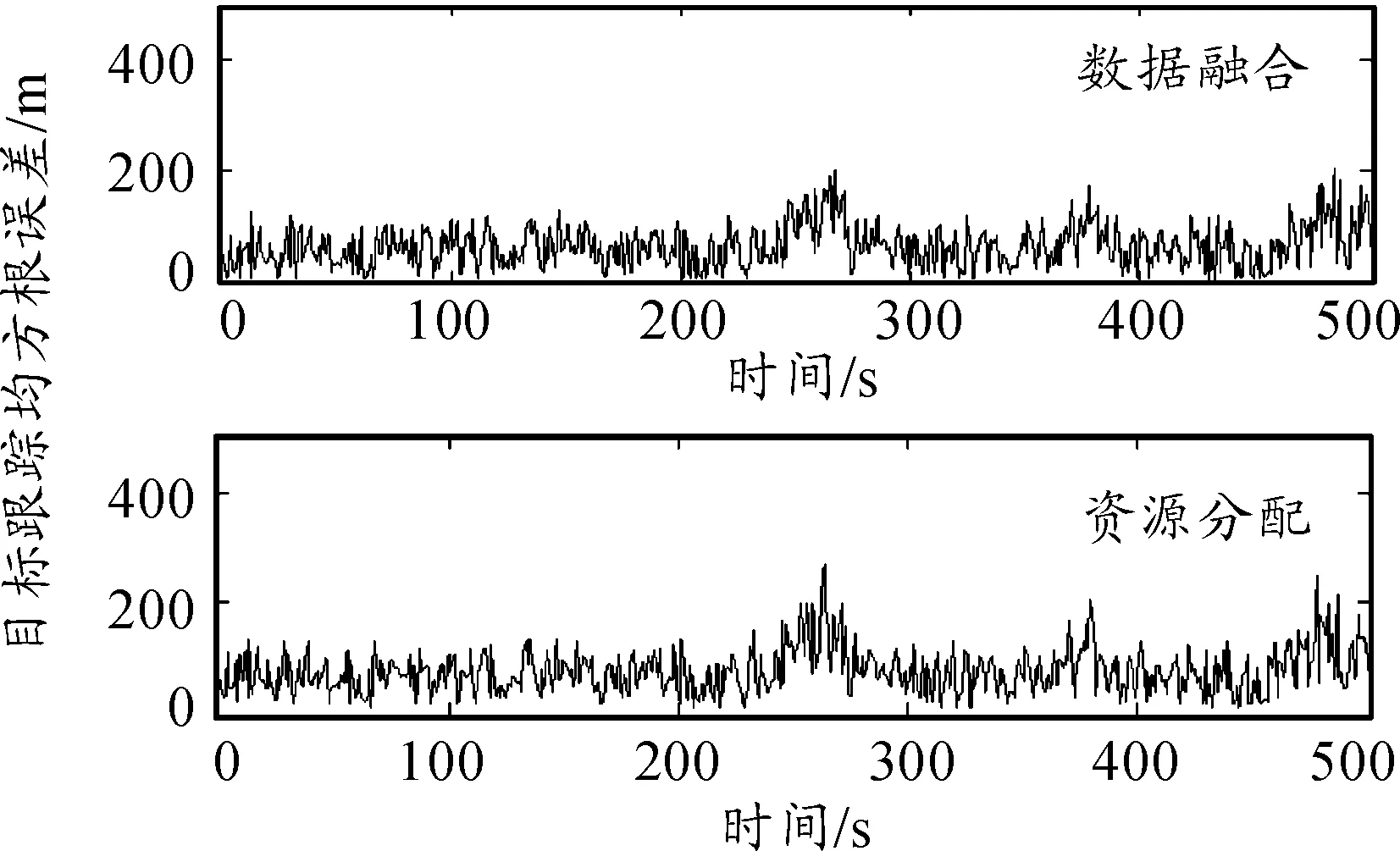
图10 目标跟踪均方根误差对比
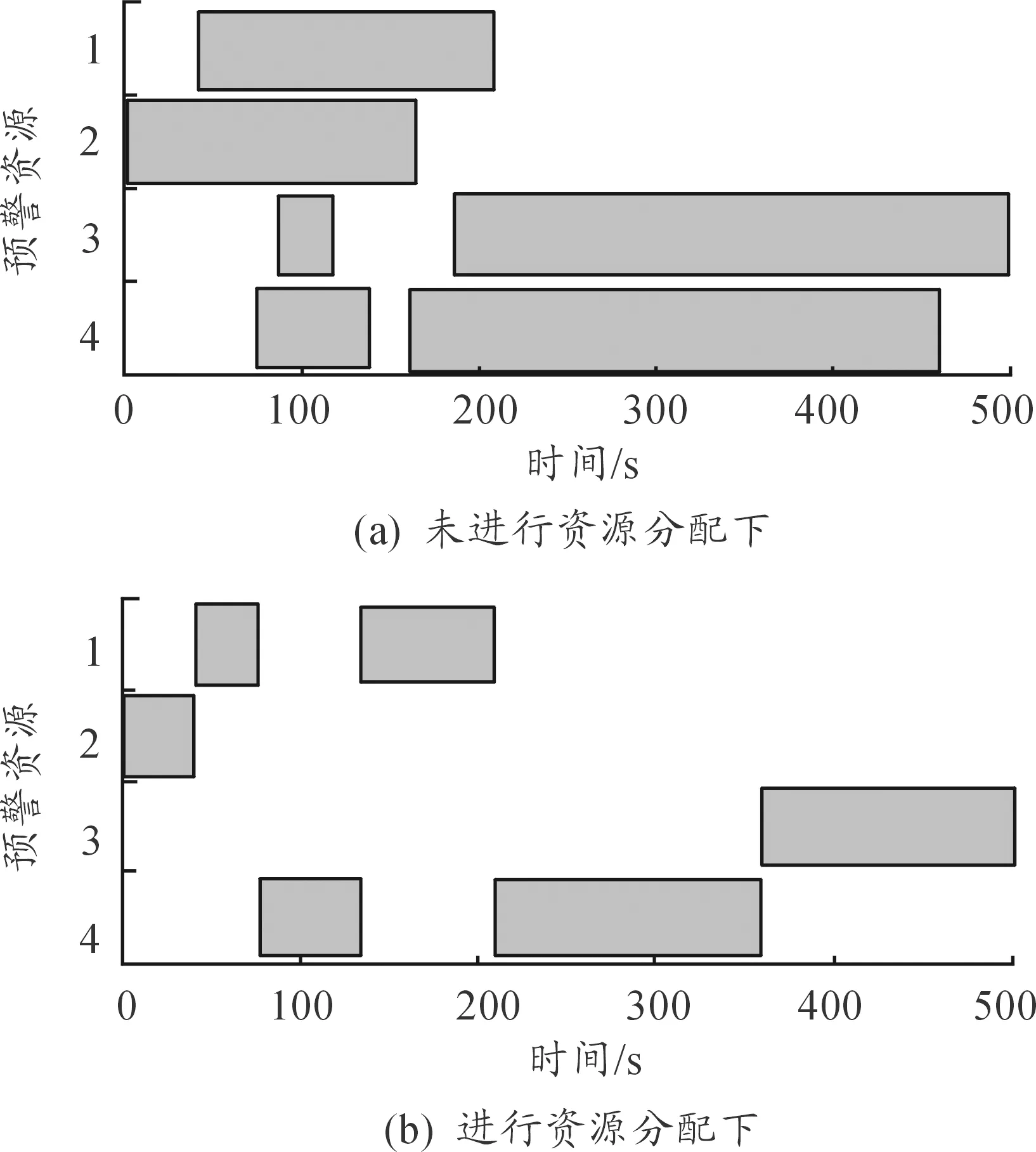
图8 资源使用甘特图
图8为两组实验的资源使用甘特图,在使用资源分配方法后,预警资源的使用明显小于未使用资源分配方法的那一组。
图9为两组实验中单位资源损耗下的信息增益对比图,由该图7可以看出:使用本文所提的资源分配方法后,资源得到了有效的利用。

图9 单位资源损耗下的信息增益对比
图10为两组实验中跟踪精度的对比图,由该图8可以看出:采用多个雷达的数据进行融合后对目标跟踪的精度较高,使用本文的资源分配方法后,目标跟踪的均方根误差并没有大幅度的增加,目标跟踪精度受到的影响不大。
4 结论
1) 通过使用本文所提方法,在对高超声速飞行器跳跃滑翔运动预警过程中,预警系统能够有效的利用资源,大大提高了资源利用率。
2) 本文所提方法不仅使资源得到有效的利用,同时保证了跟踪精度,确保预警系统完成对高超声速飞行器的预警任务。

