基于灰度模型的电能量异常数据修复研究
黄福兴 周广山 郑宽昀 冯泽佳 袁培森


摘要: 提出了一种基于灰度模型的电能量异常数据修复方法, 以经过识别的正常历史电能量数据作为输入变量, 以异常点所处的时间节点电能量数据作为输出变量, 经过一次累加, 级比检验, 求解预测方程得到预测值, 动态地对电能量数据进行迭代预测, 最终对预测值进行精度检验, 预测的平均相对残差为2.182%,根据结果对原始数据进行修改, 从而达到修复电能量异常数据的目的. 以某区域实际电能量数据进行模型预测修复, 并对结果以及误差进行分析, 验证了该方法的可行性.
关键词: 电能量; 异常数据; 灰度模型; 数据修复
中图分类号: TP391 文献标志码: A DOI: 10.3969/j.issn.1000-5641.201921016
0 引言
随着智能化、数字化、信息化电网的全面建设, 电网数据量呈几何级数增长[1], 电力行业步入大数据时代[2]. 与此同时, 电力用户对电量数据的质量要求相应提高. 电力网络中信息系统与物理系统的深度融合, 导致现代电力系统易受异常数据的影响[3]. 由于电能计量装置运行过程中, 不可避免受到各种因素的影响, 电网系统及其采集系统中会出现电能计量装置故障、配电网异常、计量装置接线错误以及采集系统档案数据错误等问题, 这些问题将影响电网的安全稳定运行和用电数据的准确采集[4]. 因此, 对各类异常数据进行及时的检测和修复是提高电量数据质量的重要措施.
大数据是信息时代的重要产物, 在智能电网运用中融入大数据, 正确掌握大数据的关键技术, 能有效推动电力行业的可持续发展以及加强智能电网的建设. 目前对于电能量异常数据的修复技术主要集中在统计学方法[5]、特征选择法[6]、插值法[7]、BP 神经网络[8] 和数据挖掘技术[9] 等.
谭子兵等[10] 提出了利用插值或站域信息冗余替换对异常数据进行修复的方法; 吕东等[11] 提出了通过对一段时间内实际采样值的拟合信号与理想状态下电力系统电气信息量进行比较, 根据其一致程度来判断采样值数据是否异常, 并按照理想信号所应遵循的规律对异常数据进行修复的方法. 王永利等[12] 提出了应用插值小波根据连续异常数据数量的不同实现可变插值尺度的数据流上的异常数据修正方法. 胡启安等[13] 对辨识出的不良数据用基于负荷特征曲线方法进行修复. 张国江等[14] 先用Kohonen 网对日负荷曲线进行聚类, 产生各类的特征曲线; 然后用特征曲线及由此产生的含有坏数据的曲线形成的样本集对BP 网进行训练, 利用BP 网的泛化能力, 使之具备对本类曲线进行坏数据精确定位的能力; 最后利用特征曲线进行坏数据的调整. 这些方法所需要训练的数据量大, 运算代价较高, 增加了系统存储负担, 对数据流的检测与修正影响较大. 钟全辉等[15] 基于灰色预测理论为电量预测可行性及方法选择等提供理论基础, 为研究提供了新思路.
灰色系统理论由中国控制论专家邓聚龙教授于1982 年首次提出, 在农业、工业、气象等领域得到了成功应用. 经过三十多年的发展, 灰色系统理论已基本建立起以系统分析、评估、建模、预测、决策、控制、优化为主体的技术体系[16], 特别是其对时间序列短、计数据少、信息不完全系统的分析与建模[17], 使用小数据集[18] 和有限信息拟合预测[19], 对数据分布依赖性较弱[20], 具有一定优势. 本文中的电能量数据系统存在一部分不确定或未知的影响因素(即灰色系统)[21], 所显示的现象是随机的、杂乱无章的, 灰度模型将看似无规律的历史数据经过累加生成后, 与原来数值相比具有较为明显的指数增长规律, 利用微分方程拟合生成后呈指数增长规律的数据列对电能量数据进行预测, 最后经累减还原成实际预测值.
本文提出了基于灰度模型的电能量异常数据修复模型, 包括级比检验、构建GM(1, 1) 模型和模型预测. 首先对电能量数据进行级比检验处理, 再利用这些原始数据进行累加生成序列, 再对建立好的GM(1, 1) 模型进行白化处理[22], 得到预测值, 通过相对残差检验对预测值进行检验, 最后使用预测值对数据进行修复. 对实际电能量数据集进行数据预测, 表明该模型具有较好的准确性及效率.
1 数据的预测修复架构
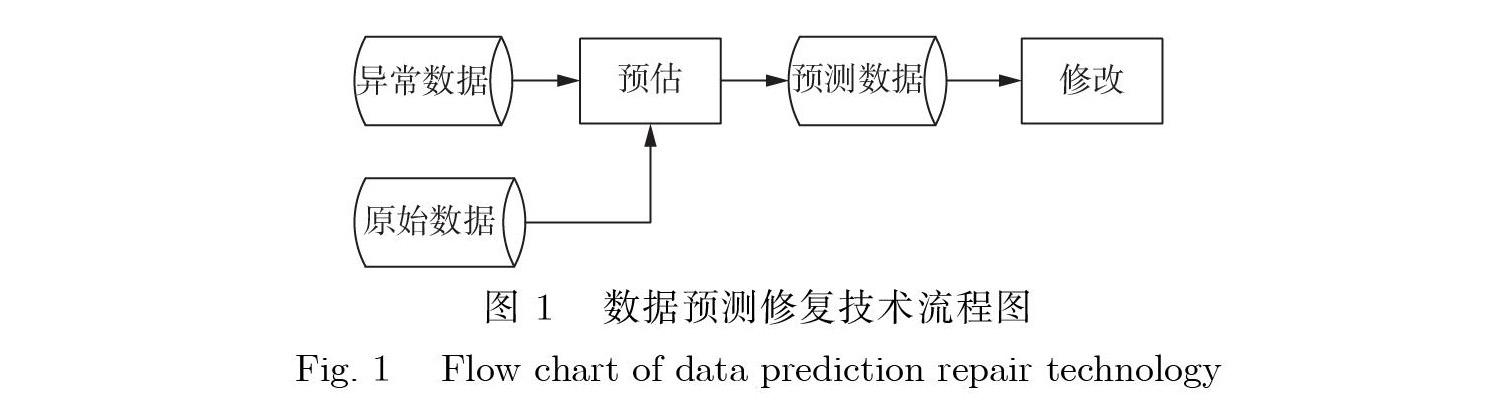
数据修复技术EE (Estimation Edit) 是指对验证为异常的数据进行预估和修改. 其规则是根据正常数据建立模型估算规则, 对异常值进行预测, 最终对异常值进行修改. 数据预测修复分为2 个阶段,流程图如图1 所示.
(1) 预估(Estimation) 是针对验证后错误的数据或遗漏数据进行对应的算法, 获得一组新的数据,例如: 线性内插法、参考日等比估算法等, 本文选取的预估模型是灰度模型.
(2) 修改(Edit) 是获得一组预测的新数据后, 决定是否将这组新数据取代有问题的数据. 在系统正常运行的情况下, 用电量普遍呈周期性变化, 在时间序列上表现为一定周期间隔后的观测点呈现一定的相似性. 本文提出的基于灰度模型的电能量异常数据修复方法中, 希望通过建立的灰度模型, 根据异常数据前一定量的正常历史数据对异常数据进行预测并替换, 实现数据的修复, 以保证数据的正确性.
2 灰度模型
灰色预测的建模主要是针对现实中存在的大量不确定性问题, 灰色预测利用少量不确定性数据即灰色数据来揭示系统未来的发展规律[23], 通过鉴别系统因素之间发展趋势的相异程度, 即进行关聯分析, 并对原始数据进行生成有较强规律性的累加数列来寻找系统变动的规律, 建立微分方程来对数据进行预测, 从而达到数据修复的目的. 在一定的预测时间段内具有较好的预测精度, 适用于原始数列非负且数据变化率较小的情况[24].
GM(n, m) 模型代表一个阶次为n、变量个数为m 的灰度模型[25]. 预测实践中发现, 提高阶次n 对预测精度提高并不明显, 而相应的计算量则成倍增加[26]. 对于本文需要修复的电能量数据来说, 因其逐渐递增且在较短时间内具有较强的规律性, 适用于n = 1 的情况, 而n = 2 适合非单调的摆动发展序列或者有饱和的S 型序列, 因此在保证预测精度的前提下, 选择n = 1. 由于需要预测的数据受时间影响, 因此相关变量为其本身的历史数据, 所以m = 1. 由此可以确定本文所使用的是GM(1, 1) 模型.灰度GM(1, 1) 模型具有建模方法简单、约束条件少、计算量小等特点[27], 不需要大量的数据, 也不必考虑数据的分布特征.
[17] 杨冠. 基于灰色系统理论的成绩预测分析 [J]. 数学学习与研究, 2018(5): 138-139.
[18]YIN K, G Y, LI X M. Improved grey prediction model based on exponential grey action quantity [J]. Journal of Systems Engineeringand Electronics, 2018, 29(3): 560-570. DOI: CNKI:SUN:XTGJ.0.2018-03-014.
[19]CHEN C. The necessary and sufficient condition for GM(1, 1) grey prediction model [J]. Applied Mathematics and Computation,2013, 219(11): 6152-6162. DOI: 10.1016/j.amc.2012.12.015.
[20]DAN M, JIANG Q Y, LI D Q, et al. Controlled-source electromagnetic data processing based on gray system theory and robustestimation [J]. 应用地球物理(英文版), 2017, 14(4): 570-580. DOI: 10.1007/s11770-017-0646-5.
[21]JUNEJO M, SHAIKH A A, QURESHI A S. Modified hybrid grey model (1,1) to forecast cellular subscribers [J]. Mehran UniversityResearch Journal of Engineering & Technology, 2018, 37(2): 439-444. DOI: 10.22581/muet1982.1802.19.
[22] 曾亮. 新时变参数灰色预测模型及其应用 [J]. 系统科学与数学, 2017, 37(1): 143-154.
[23] 杨跃东. GM(1, 1)模型的改进及其应用 [D]. 上海: 上海师范大学, 2015.
[24] 王英会. 高速公路交通流异常数据识别及修复方法研究 [D]. 北京: 北京交通大学, 2015.
[25]WANG Q, LIU L, WANG S, et al. Predicting Beijing's tertiary industry with an improved grey model [J]. Applied Soft Computing,2017, 57: 482-494. DOI: 10.1016/j.asoc.2017.04.022.
[26] 赵大同. 利用灰色模型预测用电量和用电负荷 [J]. 华东电力, 1994(10): 26-28. DOI: CNKI:SUN:HDDL.0.1994-10-008.
[27]杨保华, 方志耕, 张可. 基于级比序列的离散GM(1, 1)模型 [J]. 系统工程与电子技术, 2012, 34(4): 715-718. DOI: 10.3969/j.issn.1001-506X.2012.04.14.
[28]MAO S, GAO M, XIAO X, et al. A novel fractional grey system model and its application [J]. Applied Mathematical Modelling, 2016,40(7/8): 5063-5076. DOI: 10.1016/j.apm.2015.12.014.
[29] 鄧聚龙. 灰预测与灰决策 [M]. 武汉: 华中科技大学出版社, 2002: 244.
[30]徐宁, 党耀国. 特征自适应型GM(1, 1)模型及对中国交通污染排放量的预测建模 [J]. 系统工程理论与实践, 2018, 38(1): 187-196. DOI:10.12011/1000-6788(2018)01-0187-10.
(责任编辑: 张 晶)

