趋势面分析法在地下水动态预测中的应用

董 冬，边 静

1.吉林省地质资料馆，吉林 长春 130061；2.吉林省地质环境监测总站，吉林 长春 130021

0 引言

地下水系统经常与环境发生物质、能量与信息的交换，时刻处于变化之中。地下水动态是反映地质、水文地质条件改变的晴雨表、温度计[1，2]，因此说掌握地下水动态对于合理利用地下水或有效防范其危害十分重要。由于地下水系统的复杂性、非线性、多尺度性、突变性和随机性等本质属性的存在，使得对地下水动态预测研究变得复杂[3，4]。如何提高地下水动态预测的精度和可靠性，具有十分重要的意义。

地下水位动态预测的方法很多，但在有些水文地质条件复杂的地区，由于各种水文地质参数，源汇项及边界条件难以搞清，基于地下水动力学的预测方法并不适用[5]。趋势面分析是利用数学曲面模拟地理要素在空间上的分布及变化趋势的一种数学方法，常被用来模拟地理要素在空间上的分布规律，在空间分析方面具有重要的应用价值[6]。

1 趋势面分析的原理

1.1 趋势面分析的涵义

趋势面分析是用一个适当的数学曲面去拟合研究变量的观测值。把观测值分成两部分：一部分是趋势，它的变化受区域性因素的影响，反映观测指标在大范围内的变化特点；另一部分是剩余，它仅反映在局部范围内指标的变化特征，也受局部性因素和随机因素控制[5]。

根据研究问题的差异，有不同的着眼点：有时注重将局部因素分离出来，例如地下水污染源和地下水水化学成分异常带的圈定；有时注重研究全局性的变化趋势，例如对区域性地下水化学成分背景值的研究和地下水动态的研究。至于区域性变化和局部性变化的区分，要看研究范围的大小和目的具体确定。

根据研究的空间维数的不同，分别有一维、二维和三维趋势面分析。

用(x，y)表示观测点或取样点的平面坐标，函数z=f(x，y)表示观测值z在大范围内的变化趋势，它相对应的曲面叫趋势面。这时观测值z可表示成：

z=f(x，y)+R(x，y)

其中R(x，y)叫做剩余，它是由局部因素和随机因素所引起的观测值的变化。通常用特殊的函数形式表示趋势面函数f(x，y)，最常见的是把f(x，y)表示成各种次数的多项式，例如二元二次趋势面可表示成：

z=f(x，y)=b0+b1x+b2y+b3x2+b4xy+b5y2

这种趋势面分析叫做多项式趋势面分析。为了表示所研究变量在空间范围内的周期性变化，还可用三角多项式构造趋势面函数，这叫调和趋势面分析。由于这两种多项式可以在有限范围内任意逼近各种连续函数，因此用它们表示所研究变量的变化趋势是合适的。

把时间变量引入趋势面分析，以三维(三元)二次多项式模型的建立为例，探讨模拟预测地下水位动态的理论与方法。

1.2 趋势面模型的建立

设计算区内有L1个观测时段，L2个观测点的水位资料。任一时刻(i)，任一观测点(j)都有一个观测水位Hij和计算水位hij与之对应。因水位是位置坐标(x，y)和时间t的函数，可将水位表述成三维(元)二次趋势多项式：

h=b0+b1x+b2y+b3t+b4x2+b5xy+b6y2+b7xt+b8yt+b9t2

(1)

第i个时刻第j个观测点资料应满足(1)式，由此有：

hij=b0+b1xj+b2yj+b3ti+b4xj2+b5xjyj+b6yj2+b7xjti+b8yjti+b9ti2

(i=1,2,…,L1；j=1,2,…,L2)

(2)

式中：b0，b1，…，b9为待定系数。

实际上，由于受各种因素的干扰，观测水位Hij与趋势面计算水位hij总存在误差。即：

Hij=hij+Rij

(3)

式中：Rij为计算水位的误差。

这样就把趋势面分析问题转变为多元线性回归分析问题：

(4)

式中：k=1，2，…，n；n=L1×L2。

由最小二乘法准则，所求的多项式系数b0，b1，…，b9应使剩余平方和：

(5)

取最小值，即应满足方程组:

(6)

将方程组(6)进行整理可得如下的正规方程组：

(7)

式中：

(8)

利用地下水位的实测数据，解方程组(7)，求得b1，b2，…，b9，代入(8)式求得b0，这样就得到地下水位趋势面二次多项式，利用该三维(元)二次趋势多项式即可预报地下水位。

1.3 趋势面模型的适度检验

一般来说，任何一组水位观测数据，都可以计算出适当次数的趋势多项式。但该多项式是否能够较好地代表原始水位变量h的空间变化趋势，这个趋势多项式对水位变量h的拟合程度如何，这需要进行精度检验。

注意到趋势面分析与回归分析之间的变换关系，多元线性回归的显著性检验方法可以用于趋势面分析。采用复相关系数R检验法，将上述趋势面多项式对水位h的拟合程度进行检验。

R=u/Syy

(9)

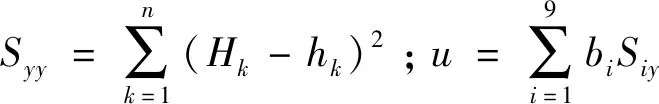
2 应用实例

以白城市热电厂抽水试验观测资料为例，建立地下水位动态三维(元)二次趋势面多项式，并预测地下水位动态。

2.1 趋势面模型的拟合

用5个观测孔，10个时刻的地下水位观测资料进行模型的拟合，建立地下水位降深趋势面多项式模型为：

S=-0.173-0.559x+0.422y+0.292t+0.008x2+0.012xy-0.012y2+0.001xt+0.000 1yt-0.024t2

(10)

拟合结果令人满意，相关系数R=0.977，经检验x、y、t与S的显著性强。计算的水位降深和观测水位降深曲线基本吻合，见图1。这说明建立的地下水位动态三维(元)二次趋势面多项式模型(10)反映了拟合时间段内水位随时空的变化规律。

图1 5号孔地下水位降深计算值与观测值对比曲线Fig.1 Comparison curves of groundwater drawdown calculation value and observation value of No.5 hole (10)

2.2 地下水位动态预测

建立地下水位动态三维(元)二次趋势面多项式模型的目的是预报地下水位动态，三维(元)二次趋势面多项式的可靠性和适用程度如何，关键要看预报的结果。

采用此方法预报其中的3个观测孔，8个时刻的地下水位动态，预测结果令人满意，计算值与实际观测值比较接近，预测结果见表1。说明该预测方法是可靠和适用的。

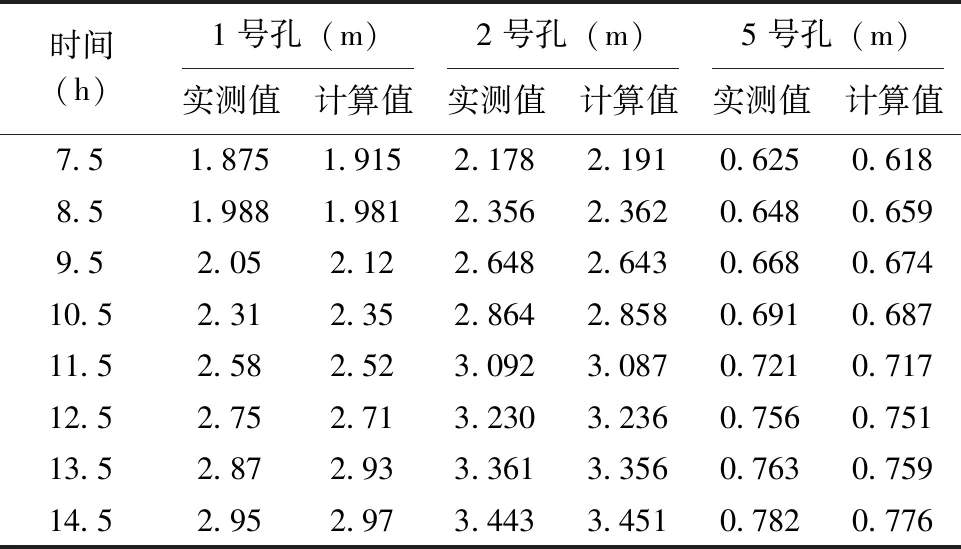
表1 预测与实测地下水位降深对比表Table 1 Comparison between drawdown of predicted groundwater level and that of measured groundwater level

3 结论

(1)地下水位动态三维(元)二次趋势面多项式模型既可内插水位，也可预测地下水位动态。该预测方法使用于水文地质条件复杂、难以搞清，数学模型难以确定的地区。

(2)趋势面分析法模拟预测地下水位，要求有足够长序列的地下水动态观测资料，预测与拟合的条件完全相同。

(3)算例中，三维(元)二次多项式xt和yt项系数很小，说明其与水位的关系不密切，如果采用逐步回归，剔除这些不显著项，效果会更好。

(4)应用此法预测地下水位动态只是做一点探索性的尝试，尚不成熟，有待进一步研究完善。但可以预想，应用此法来模拟预测水污染和水化学成分异常可能意义更加深远。