基于模糊聚类的电力专家故障诊断信息融合方法

王 平，张 勤

(1.四川天一学院 信息工程系，四川 绵竹 618200 ；2.西华大学 电气与电子信息学院， 成都 610039)

0 引 言

随着传感器技术、计算机技术的不断发展完善,很多电力设备上都安装了自动化程度高、运行速度快的数据采集、检测系统[1]，这类系统的使用大大地提高了测试、检查的效率，对电力设备的安全运行发挥了重要作用。目前电力系统的故障检测和识别通常由专家完成，当设备出现故障后，需现场的技术人员和专家，根据检测报警信号、设备的故障现象和工作经验来诊断分析故障原因，提出故障解决方法。近年来，随着人工智能技术的发展，专家系统、模糊推理、人工神经网络、模拟退火、遗传算法等方法被引入电力系统故障诊断过程，取得了大量的研究成果[2]。模糊聚类用于电力故障的诊断，如基于模糊聚类分析的燃气轮机振动故障诊断研究[3]、基于模糊综合理论的电力变压器故障诊断[4]、加权模糊核聚类法用于电力变压器故障诊断[5]、模糊神经网络用于电力系统电压稳定评估[6]等研究成果，推动了模糊聚类算法在电力故障诊断中的应用。本文提出一种动态模糊聚类方法，以对多位专家的故障诊断推理进行信息融合，尽快识别和排除故障。

与单一信息源检测系统相比，多源融合所提供的信息具有相关性、互补性和冗余性，信息融合就是对上述三种信息特征的不同处理过程[7]。对来自多个专家诊断信息的融合可以降低故障系统识别的误差和不确定性、提高故障检测的概率和识别的准确度、提高系统输出结果的可信度，从而提高系统的性能。因此，结合故障现象和专家经验，利用多源信息融合方法，实现故障实时在线检测诊断与恢复是电力监控设备的一个重要发展方向。本文提出基于模糊聚类进行电力故障的诊断，以实现电力故障的快速诊断和恢复。

1 专家故障诊断结果的动态模糊聚类融合方法

1.1 专家故障诊断结果的模糊化方法

基于专家诊断信息的电力设备故障检测与诊断是一个故障从模糊到逐渐清晰并慢慢得到正确识别的过程，在这一过程中，需要不断结合故障现象和不同专家的意见进行多次融合识别。尽管每次识别参与的专家和结果可能不一致，但每次识别结果都能够通过专家意见分析以概率形式表现出来。为了尽快确定故障、进行故障恢复，需要判断各次结果是否一致，以确定故障原因、决定应对策略。为了解决这个问题，可以通过模糊聚类分析方法判断专家集体对故障的识别结果。

由于故障融合识别的输出结果可能为故障库中的任何一个已知故障类型，可以表示为故障现象隶属于某一种类型故障的概率，因此，对这些数据应该使用连续型的隶属函数来分析。由于每次故障识别的结果都是专家诊断意见的概率表达，因此，在专家来自于同一或相近领域的情况下，他们的结论应该比较接近。由于故障识别是一个渐进识别的过程，其识别结果与故障原因相符的概率呈不断增长的趋势，于是，可以假设经故障识别后的故障概率服从先小后大的S型曲线分布，即服从以下分布：

假如已知经过n次专家故障诊断得到故障现象为第i类的概率(即故障现象隶属于某一已知类型故障i的隶属度)分别为xi1，xi2，…，xin。则需要对n次专家诊断结果进行分析，以得出故障原因为某一类型故障的概率。

由于在多次识别运算的结果中，有可能出现较大的误差值，因此，不能直接取这些概率的平均值作为输出结果，否则可能由于存在偏差很大的数据而改变正确输出值，导致故障识别错误，因而不能在上述分布公式中取n个数据的平均值作为a，同样也不能取n个数据的标准差作为b，即

为了利用多次专家诊断的结果产生一个正确的结果，求取的过程不仅要进行取粗存精，而且要进行数值的比较。虽然对于各次专家诊断产生的i×n个判断，不能确切地知道哪些判断最接近于故障的实际情况，但是可以利用动态聚类方法分析诊断结果集中于哪些故障原因，然后推断和识别出故障。

由于多次专家诊断得出的意见，其变量单位和量级可能是不一样的，直接用原始数据进行计算会突出那些绝对值大的变量而压低那些绝对值小的变量，所以，在进行聚类分析之前，需要将原始数据进行标准化处理。为此采用下面的标准差标准化方法：

(1)

其中：

分别为第k个变量的平均值和标准差。

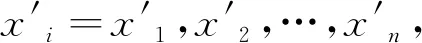
(2)

对于a值，采用轮换方式，即分别对a取x1，x2，…，xn来进行运算，求取其他各值相对于a的隶属度。将求得的隶属度写为矩阵形式，即

这里主对角线的元素为1，表示元素隶属于本身的隶属度为1，即完全隶属于自己。

1.2 故障识别的动态模糊聚类方法

为了利用聚类方法找出专家诊断结果的一致意见，得出正确的聚类输出结果，利用下面的动态聚类方法来对这些隶属度进行分析，求取专家故障识别结果的聚类过程如下：

1) 利用隶属度矩阵A使用传递闭包方法求出其等价模糊隶属度矩阵：

t(A)=A2k

2) 设定最小λ值，对于大于此值的模糊隶属度，根据等价模糊隶属度矩阵中的元素值的大小排列，依次将其设为λ，利用动态聚类方法进行聚类。

3) 若聚类数据中某一聚类中心集聚数据个数达到1/2以上，则停止聚类；以此聚类中心集聚数据的平均值作为对象为某一目标i的概率Pi，以供决策参考。

4) 若没有一个聚类中心集聚数据个数达到1/2以上，说明这些识别结果不一致，需要进行更多次专家诊断信息采集和识别，才能确定是某一类型故障及故障的概率。

若识别对象是多个故障类型i=1，2，…，n中的某一类，则重复上述步骤分别求取P1，P2，…，Pn，取最大值Pi，认定该故障源为故障i。

2 变压器故障专家诊断的模糊聚类信息融合

以某变压器故障诊断过程为例说明应用该方法的聚类过程。假设变压器发生了过热故障，针对故障现象，组织不同的工程师和维修技师进行分组讨论，并识别故障源和故障类型，经过6次专家分组讨论，一致认为故障可能由下列3个原因产生：铁心片间短路(故障A)；分接开关接触不良(故障B)；部分绕组短路(故障C)。各专家小组讨论识别结果如表1所示。

表1 专家小组多次故障诊断的结果

如果采用加和归一化方法，则A、B、C 3个故障的概率加和分别为

P1=0.60+0.85+0.92+0.67+0.72+0.73=4.49

P2=0.72+0.85+0.86+0.89+0.86+0.85=5.03

P3=0.50+0.91+0.73+0.62+0.45+0.85=4.06

归一化后，得出

P1′=0.33，P2′=0.37，P3′=0.30

可以推出故障B的可能性比故障A和 C更大一些，但不是很明显。

根据上述聚类过程，对这些数据使用标准差方法进行标准化。首先选取故障A的融合识别结果进行分析。

其中：

求得x11=-1.38，x2=0.95，x3=1.60，x4=-0.73，x5=-0.26，x6=-0.17。利用式(2)使用a值轮换方法求各值之间的模糊隶属度,将这些数据之间的模糊隶属度写成矩阵形式，得

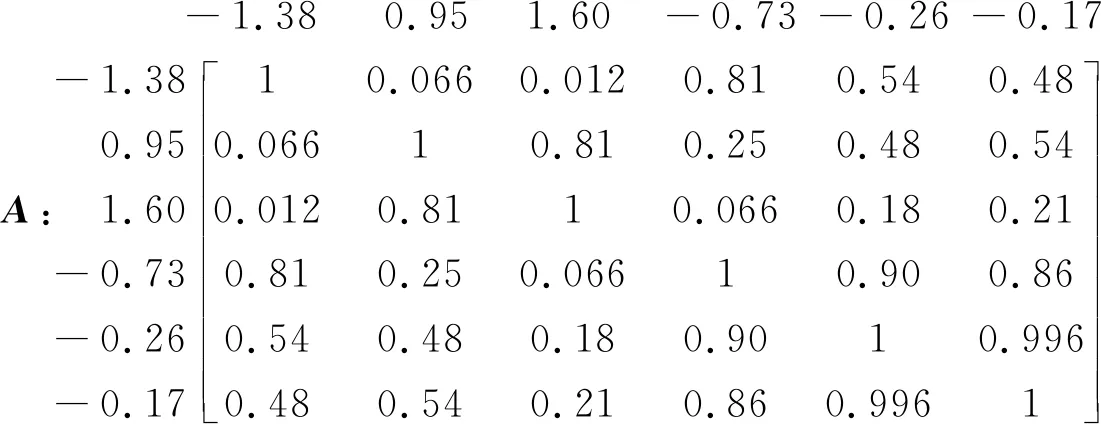
矩阵外的行和列为对应行和列的值，矩阵中的每一个元素代表对应行值和列值之间的模糊隶属度，求此矩阵的等价模糊隶属度矩阵，得

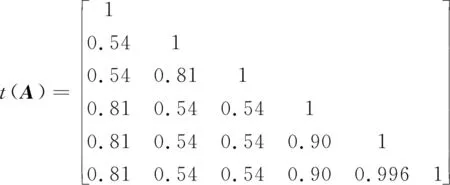
当λ=1时，可将U分为6类：{x1}，{x2}，{x3}，{x4}，{x5}，{x6}。

当λ=0.996时,可将U分为5类：{x1}，{x2}，{x3}，{x4}，{x5，x6}。

当λ=0.90时：

可将U分为4类：{x1}，{x2}，{x3}，{x4，x5，x6}。

当λ=0.81时：

可将U分为2类：{x1，x4，x5，x6}，{x2，x3}。

当λ=0.54时，所有数据归为一类。

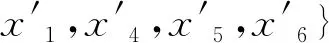
对各专家小组的故障识别结论进行聚类分析的结果认为故障原因是故障A(铁心片间短路)的概率P1为0.68。

同样经上述分析步骤，可得故障原因是故障B(分接开关接触不良)的概率P2为0.86；是故障C(部分绕组短路)的概率P3为0.58。归一化后得P1′=0.32，P2′=0.41，P3′=0.27。由于P2′>P1′>P3′，经过上述模糊聚类故障识别过程后，认为专家的综合意见是故障B(分接开关接触不良)的可能性更大，所提方法相比于简单加和归一化方法，明显突出了故障B的概率，P2′从0.37增加到0.41，P1′和P3′降低，减少了故障诊断的不确定性。

3 结 语

所提方法首先对专家故障诊断的结果进行模糊化处理，得出专家识别为某一故障的概率，再对专家诊断的原始数据进行标准化处理，求取标准化后的各值之间的隶属度，最后利用动态调整λ截集的聚类方法进行聚类，得出每一可能故障源的故障概率，根据多数一致性原则做出故障诊断结论。应用动态模糊聚类分析法可以解决在故障识别过程中专家意见多样化的问题，根据聚类分析结果能够得出大多数专家的一致性意见，有利于实现正确的故障诊断，尽快完成故障的恢复。