计及线路故障率时变特性的电力系统短期可靠性快速评估

邓奥攀，许宇翔，卢 海，何泽斌，邱 烜，胡 燃

(广东电网有限责任公司广州供电局，广州510000)

0 引 言

电力系统短期可靠性指标是运维部门决策的重要参考依据[1-2]。对电力系统短期可靠性进行预测，有助于提前发现系统的脆弱环节，并采用针对性策略进行优化，从而极大地降低电网风险和提升系统可靠性。因此，迅速精确地预测系统短期可靠性水平具有重大的现实意义[3]。

系统元件可靠性参数和节点负荷是评估系统可靠性的关键数据，该数据的全面性决定整个系统短期可靠性评估的准确性[4-5]。文献[6]指出元件故障率和修复率会对系统可靠性评估产生直接影响，即元件停运模型建模不准确，将导致整体评估结果出现较大偏差。文献[7]把天气情况分为正常、异常、恶劣3种类型，并利用联系数法分别建立了3种天气情况下的元件故障率模型，分析结果表明极端天气对系统可靠性有较大影响。此外，在系统长期可靠性评估中，一般假定可靠性参数为恒值，并将系统的负荷设定为单一水平，因此,其评估结果难以反映可靠性水平随时间和外部环境的变化情况[8]。在短期可靠性评估中，由于系统拓扑结构基本不改变，因此,元件可靠性变化和负荷波动是影响可靠性水平的关键因素。综上可知，建立元件可靠性参数时变模型对于提升系统短期可靠性的精确度十分重要[9]。

随着电力系统持续建设和不断发展，系统中元件数目呈几何级数增长，而由于元件故障率和负荷处在动态变化中，当利用传统方法进行系统短期可靠性评估时，为减少评估误差，需要反复进行仿真计算，消耗相当长的时间，难以满足系统实时调度的时效性要求[10]。

针对这一问题，提出一种系统短期可靠性快速评估方法。该方法首先对近几年输电线路故障率月度分布统计数据进行参数拟合，求取故障率连续时间函数以获取任意时刻故障率。然后分析线路故障率变化与负荷波动对系统可靠性影响。此外，通过回归分析法构造基于线路故障率和负荷的系统可靠性指标非线性函数，将线路故障率及负荷实时值代入该非线性函数，通过代数方法便能快速获取系统短期可靠性评估指标。最后，应用传统方法与所提出的新方法对改进IEEE-RBTS系统在极端天气下进行短期可靠性评估，通过对比分析验证所提方法的快速性。

1 时变故障率模型

1.1 故障率月度分布

作为电力系统中的重要组成部分，架空输电线路由于长期直接暴露在户外，其运行工况会在很大程度上受到外部环境影响，致使输电线路故障率随着气象的周期变化呈现出周期性，而并非恒定不变。由于不同年份相同月份的气象条件大体呈现出相同的发展和变化趋势，因此，在进行系统短期稳定性分析时，可以根据往年的月度统计故障率，作为当年同期月份的故障率预测值。借鉴文献[11]方法建立线路时变故障率模型。

根据故障率的定义，单回架空输电线路的同期故障率为

(1)

式中：λi(m)为线路i在历史同期的第m月的平均故障率，单位为次/(100 km·月)，可换算为次/(100 km·年);Nkim为线路i在第k年m月的故障次数；k为统计的总年数；Li为线路i的长度，单位为100 km。

在进行故障率计算时，如果只统计某条线路的历史故障率并代入计算，则由于样本数量十分有限，不利于精确估计样本的分布。因此,为提高预测精度，将同一地区相同电压等级规格的其他输电线路的同期故障率纳入参考范围，并依据下式计算同一电压等级规格线路的同期月故障率：

(2)

依据式(1)和式(2)，统计沿海某市近5年220 kV电压等级架空输电线路历史同期的故障数据，得到线路故障率月度分布，结果如图1所示。

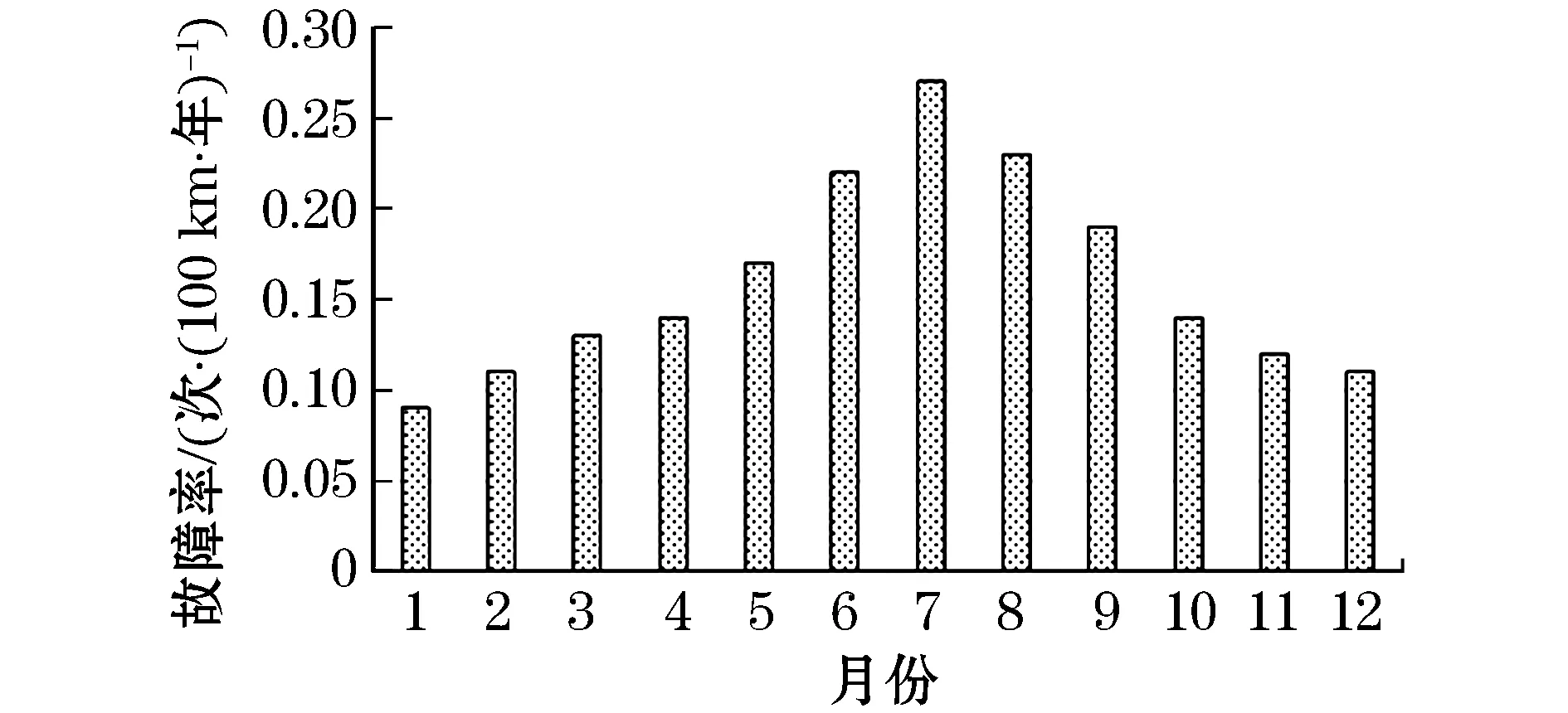
图1 某沿海市220 kV输电线路故障率分布

1.2 故障率连续时间函数

在电力系统短期可靠性评估中，为保证评估结果的准确性，需获取任意多个时刻的线路故障率数据。因此，在连续的时间坐标上，建立了架空输电线路故障率的分布函数模型，并采用傅里叶函数和高斯函数对离散的月度故障率数据进行参数拟合，得到相应的分布函数。

一次傅里叶函数表达式为

f(x)=a+bcos(wx)+csin(wx)

式中：a、b、c和w为傅里叶函数的拟合系数。

其中，n为统计年限，xi是第i年的年雷暴日，x¯为所统计的63年内年平均雷暴日，t¯为自然数序列的平均值，用公式表示为t¯=（n+1）/2，rxt的正（负）值表示该要素在所统计年限内有增加和减少的趋势，rxt绝对值越大表明该要素增加和减少的程度越明显，即表示气候变化趋势越明显［5］。

单项高斯函数表达式为

二项高斯函数表达式为

(3)

式中：A、B、C,A1、B1、C1,A2、B2、C2均为为高斯函数的拟合系数。

以图1中线路故障率数据(已做归一化处理，其值为月架空输电线路故障率与年平均故障率比值)为样本，分别采用傅里叶函数、单项高斯函数及二项高斯函数进行拟合，其拟合结果如表1所示，相对应的拟合曲线如图2所示。

表1 输电线路故障率拟合效果

图2 输电线路故障率拟合曲线

表1中：R-square为拟合优度，其值越接近1代表拟合效果越好；RMSE为均方根误差，其值越接近0代表拟合效果越好。

由表1和图2所示的拟合结果，通过对比分析可知，二项高斯分布函拟合效果最好，更能突出曲线峰值，也更贴合该沿海地区6～9月台风高发致使输电线路故障率显著增大的特征。单项高斯分布函数由于形式简单，可调整的参数最少，因此，在3种分布函数中拟合效果较差。

此外，拟合效果与样本数相关，历史同期样本数越多则越能表征整体分布规律。拟合系数并非恒定不变，随着样本数据增加而调整相应的拟合系数，能够更好地表征架空输电线路故障率分布规律。

2 快速评估

2.1 样本获取

基于上述时变故障率模型，采用蒙特卡洛算法对改进的IEEE-RBTS[12]标准系统进行仿真。该系统含有6条母线，其中发电侧共11台发电机组，总装机容量为240 MW；负荷侧有9条230 kV输电线路，共5个负荷节点，峰值负荷为185 MW。该系统具有发电侧充裕度和输电侧充裕度较为平衡的特点，更能体现输电线路故障率对系统可靠性的影响。

为更全面地模拟实际情况，在仿真初始阶段，首先将RBTS系统所有线路年平均故障率降为初始值的1/10。改进后的IEEE-RBTS系统部分线路故障率如表2所示。

表2 输电线路可靠性数据

表3 不同负荷和线路故障率下的EENS

2.2 回归分析

为构造线路故障率、负荷和可靠性指标三者之间的非线性函数，对60组EENS样本进行回归分析，对比多组拟合函数的拟合优度，选取如下式所示的最优回归方程：

式中：ai(i=0,1,…,6)为常数；x1和x2为自变量，分别代表负荷和线路故障率的标幺值；y为因变量，为系统可靠性指标EENS的标幺值。

x1最高为3阶而x2仅有1阶，因此相较于x2，x1对y影响更大，这也符合负荷变化对系统可靠性水平影响更大的实际情况。最优回归方程的回归系数估计值及其置信区间如表4所示，相对残差分布和回归方程曲面分别如图3和图4所示。

表4 回归分析参数取值和置信区间

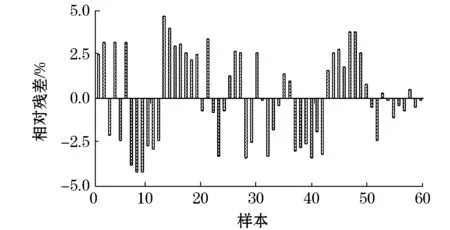
图3 数据样本和回归函数预测值相对残差

图4 回归方程曲面

由图3和图4可知，各样本与回归函数预测值相对误差均小于5%，且样本能较好地落在回归方程拟合曲面中，表明回归分析构造的函数能准确地反映系统可靠性指标随线路故障率和负荷的变化规律。

从图4负荷轴观察可知，负荷水平较低时系统可靠性指标较低，通常负荷水平低于峰值负荷55%时，系统可靠性指标极低；相应地，当负荷水平增至峰值负荷75%时，系统可靠性指标迅速增加；在负荷维持在峰值的75%至100%阶段时，曲面呈指数变化趋势。负荷与可靠性之间呈现出上述规律，因当用户所需的电能即负荷较小时，即使输电侧设备出现故障致使部分电能损失，剩余电能供给仍能满足用电侧的负荷需要，因此系统充裕性较高，可靠性指标较低；而当负荷水平较高时，输电侧如出现输电线路故障，造成电能传输阻塞，系统将损失部分负荷，因此系统充裕性低，可靠性指标较高。

同时，从图4线路故障率轴观察可知，线路故障率升高将致使可靠性指标升高，但对系统可靠性指标影响程度较小。因输电线路只是众多设备之一，虽然故障率受外部环境变化较大，但发电机组和变压器等其他设备故障率短期内变化较小。

3 评估流程

基于上述建立的线路时变故障率模型和构造的可靠性指标求取代数方程，提出了短期可靠性快速评估方法，评估流程如图5所示。

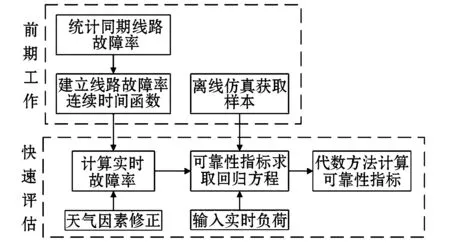
图5 短期可靠性快速评估流程

4 算例分析

为验证此电力系统短期可靠性快速评估方法的正确性和快速性，分别应用该方法和传统方法对改进的RBTS系统在极端天气下进行24小时短期可靠性评估。算例中输电线路年故障率平均值如表2所示，故障率连续时间函数符合式(3)所示的二项高斯函数分布，且在进行故障率计算时，为提升计算精度，需要将对故障率影响较大的降雨天气纳入考虑范围，不同降雨量下线路故障率变化值及24小时降雨量分布采用文献[13]数据，分别如表5和图6所示，其中日负荷曲线也绘制在图6中。将降雨量、负荷大小以及时变故障率纳入考虑范围，利用两种方法分别计算得到的EENS如图7所示，两种方法计算时间如表6所示。

表5 不同降雨量下线路故障率变化值

图6 负荷和降雨量24小时分布曲线

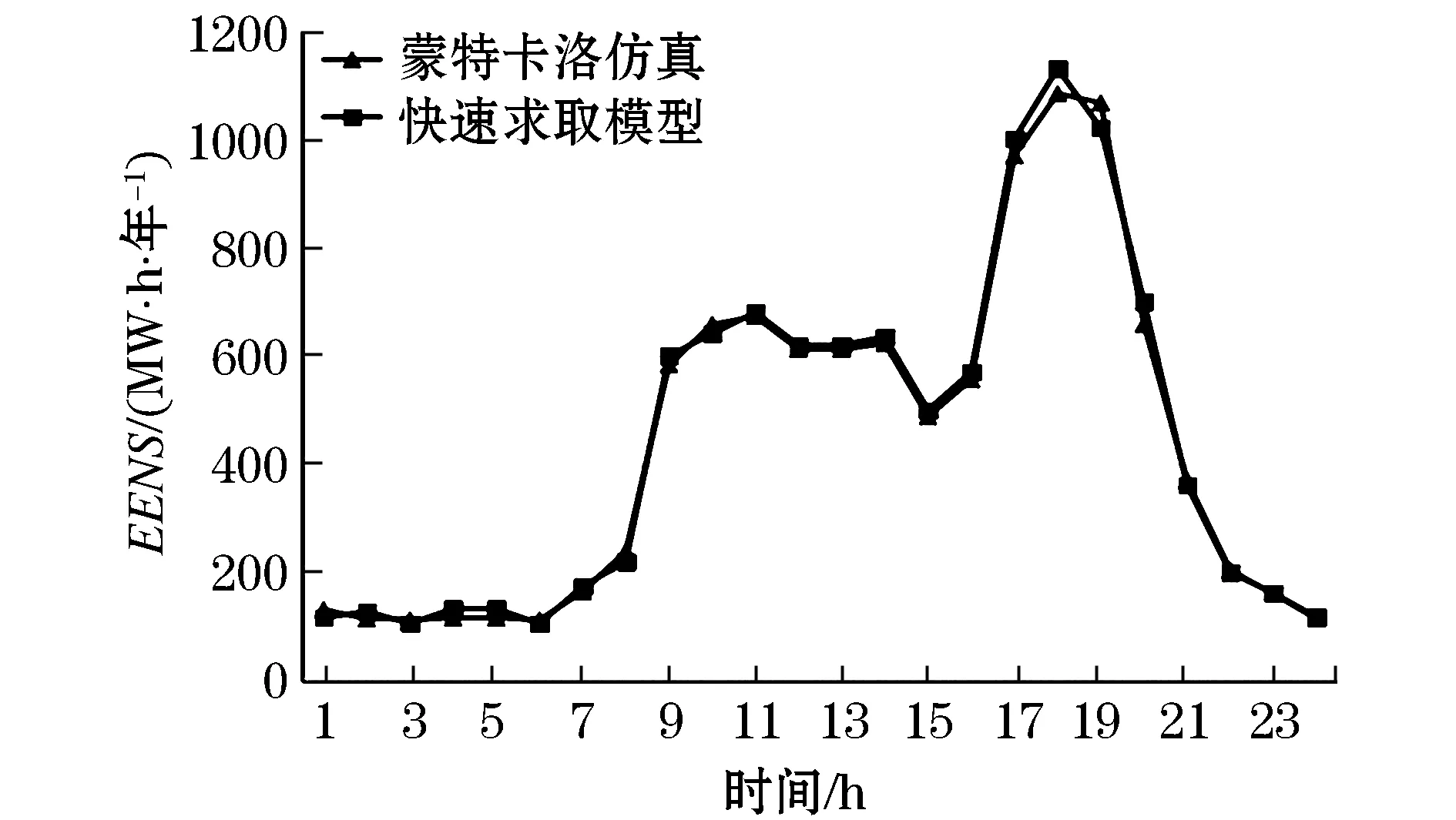
图7 不同方法求取的EENS

表6 不同方法的计算时间

由图7和表6可知，两种方法求取的EENS指标十分接近，即此短期可靠性快速评估方法具有较好的精度。相较于每次评估均需耗时几分钟的传统仿真方法，该方法在前期已将仿真计算一次性完成。每次进行系统短期可靠性评估时，只需计算线路实时故障率和获取负荷，代入回归方程即可求出可靠性指标，不再需要仿真计算，实际耗时仅为简单的代数计算过程，达到了快速预测系统短期可靠性水平的目的。

5 结 语

1)输电线路时变故障率拟合效果与样本数相关，历史同期样本数越多则越能表征整体分布规律。因此，需对地区相同电压等级的架空输电线路故障率进行详细统计。

2)相较于输电线路故障率变化，系统负荷波动对系统可靠性水平影响较大。

3)与传统方法相比，此可靠性快速评估方法仅通过代数方法便能求取系统短期可靠性指标，在保证计算精度的条件下能更为快速地评估系统短期可靠性水平。