基于多尺度模型的斜交相贯节点基本力学性能分析
王 璐,史庆轩,戎 翀
(1.广东海洋大学 寸金学院,广东 湛江,524003;2.西安建筑科技大学 土木工程学院,陕西 西安 710055)
斜交网格体系是一种新型结构体系,因其独特的结构特点和美观的建筑外表,在现代建筑结构中的应用越来越广[1].最早使用此种结构的是2004年在伦敦建成的瑞士再保险塔,其次是美国纽约的赫斯特大厦、多哈的卡塔尔外交部大楼.在国内,于2009年在广州建成的广州西塔首次使用此种结构形式,其次是CCTV新大楼、大连的中石油大厦、深圳创投大厦等等均采用了这一集受力与建筑美学于一体的斜交网格结构.这种斜交网格结构采用交叉布置的斜柱替代常规结构中的垂直柱系统,其具备同时承受结构竖向和侧向荷载的高效机制, 但该种结构体系延性较差[2-3].国内外学者对斜交网格结构的研究主要是利用有限元软件建立宏观模型进行整体受力性能分析,很难反映节点受力以及破坏的详细过程;而节点连接是受力的关键部位,目前关于节点的受力破坏和抗震性能研究主要是利用有限元分析软件建立斜交网格相贯节点三维实体单元模型,其虽可以较好把握局部破坏过程,但计算量较大,收敛性差[4-5].故工程计算迫切需要提出一个可以同时模拟结构局部微观破坏和整体宏观行为的计算模型,而多尺度计算就是解决该问题的有效途径.
多尺度分析模型是基于尺度分离思想的计算模型,即根据结构构件或节点的复杂程度和破坏过程中的非线性程度,选择适当尺度的分析模型,通过合适的连接方式,实现不同尺度模型之间的协同计算,最终既可以把握结构的整体受力特征又能反映节点实际的受力情况[6].多尺度分析模型可在精度和计算代价之间寻求一个较好的平衡点.
基于以上尺度分离思想,本文将对某一圆钢管混凝土斜交相贯节点进行多尺度的分析计算对比,验证多尺度分析模型的合理性和准确性.由于方钢管混凝土构件便于施工处理,稳定性好,具有良好的抗震性能和延性性能[7-8],应用前景广泛,故应用到轴向受压的斜交相贯节点多尺度模型中,结果表明,本文提出的连接方法能够保证关键节点的计算精度,可以很好地模拟钢管混凝土节点的受力情况,从而为建立适用于高层建筑斜交网格筒结构的多尺度分析模型提供参考.最后基于相贯节点多尺度分析模型,对影响方钢管混凝土斜交相贯节点荷载-位移关系曲线和节点承载力的主要参数进行分析,并得到了各参数对其力学性能的影响规律.
1 模型的建立
斜交网格结构体系节点实验模型中,四根钢管在椭圆连接板处相交,并将四根钢管与椭圆连接板焊接在一起,椭圆连接板厚度为两倍的钢管壁厚,钢管之间的角度为α(α=10~ 90°).在四根圆钢管相交的中心平面形成圆钢管焊接焊缝处有焊接的环向加强板存在,并且环向加强板上、下方的圆钢管上焊接衬板,加劲肋板分布均匀地焊接于环向加强板与环板之间[4-5],如图1所示.
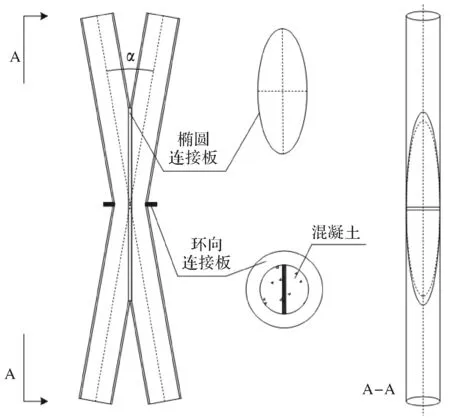
图1 斜交网格节点构造Fig.1 Joint of diagrid structure
在研究中,利用梁单元钢管和混凝土的本构模型结合有限元分析软件ABAQUS的隐式算法,基于ABAQUS平台的钢与混凝土结构纤维模型子程序iFiber LUT模拟[9],对钢管混凝土进行模拟.基于ABAQUS平台所建立的多尺度有限元分析模型如图2所示,斜交网格节点多尺度模型主要由杆系单元与受力关键部位的实体单元组成.杆单元与实体单元的界面连接的关键在于寻找适当方法实现界面处节点数量不对应情况下的变形协调[10],如图2所示.由于不同尺度模型之间在变形后各点位移一致,可以在ABAQUS中利用Interaction中的Coupling连接功能实现界面耦合,保证结点与连接界面之间转动以及横向位移协调.
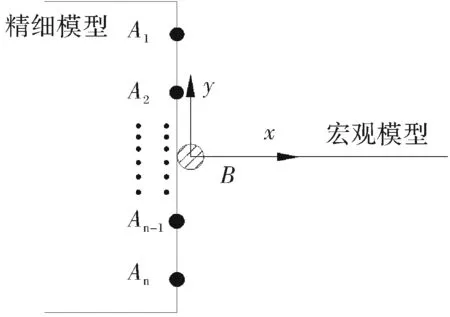
图2 多尺度模型耦合示意图Fig.2 Multi-scale model coupling diagram
如图3所示,本文主要建立了两种多尺度模型,其中核心混凝土采用实体单元,单元类型为C3D8R;钢管采用壳单元,单元类型为S4R;其余部分用梁单元建模,单元类型为B31,钢管采用rebar离散钢纤维模型;模型建成后进行网格划分,核心区域网格划分较密,杆件区域则划分较疏;通过对国内外斜交网格相贯节点研究进行分析[11-12],可得节点区对杆件区域的影响范围为1.2倍的构件截面宽度,故取多尺度耦合界面位置为1.2B(B为构件截面宽度).
对于钢管与核心混凝土界面法向方向的接触采用“硬接触”,即垂直于接触面的压力可以完全地在界面间传递.而对于钢管与核心混凝土界面切向力模拟采用库伦摩擦模型,摩擦系数μ=0.6.钢管与混凝土之间的平均界面粘结力,对于圆钢管混凝土可根据Roeder(1999)[13]的研究成果,按下式计算:
τbond=2.314-0.019 5·(d/t)
(1)
其中,d为核心混凝土的直径;t为钢管壁厚.方钢管混凝土的平均界面粘结力,根据Morishita等[14]的研究成果,约为圆钢管混凝土的0.75倍,因而对于方钢管混凝土,可按下式计算:
τbond=0.75[2.314-0.019 5·(b/t)]
(2)
其中,b为核心混凝土的边长.
模型中忽略了节点区域的焊缝以及焊接残余应力的影响,在焊缝处采用Tie将钢管与环板以及衬板连接为一个整体.
假定斜交网格柱柱脚固结,约束X、Y、Z方向的平动与转动;而在斜柱顶端沿轴向施加荷载,为了得到钢管混凝土相贯节点轴压荷载-变形关系全过程曲线,计算时采用位移控制的对称加载方式.

图3 有限元多尺度模型Fig.3 Finite element multi-scale model
2 材料本构模型的选取
2.1 混凝土本构模型
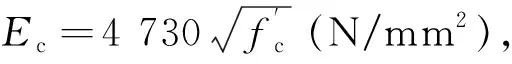
在钢管混凝土中,钢管的约束作用使得钢管内的核心混凝土属于约束混凝土,其延性以及承载力不同于普通混凝土.以往研究表明,约束混凝土的塑性会有所增加,主要表现在两方面:(1)对应峰值应力的应变有所增加;(2)应力-应变关系曲线上的下降段趋于平缓[15].
对于钢管混凝土实体模型,本文基于双剪统一强度理论[16],提出的约束混凝土实用应力-应变关系模型,以反映钢管混凝土在受力过程中产生的被动约束力对混凝土性能的影响,表达式如下.
(3)
式中:x=ε/εcc,ε为应变值;y=σ/σc,σ为应力值;αa为上升段参数,αa=2.4-0.0125σcc;n为下降坡度系数,n= 1+exp(-3ω),εcc为约束混凝土峰值应变,计算公式为
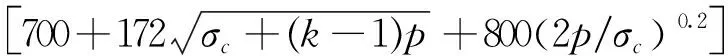
(4)
(5)
对于圆钢管混凝土,D为钢管外径,σc取混凝土圆柱体单轴抗压强度,p= 2tfy/D;对于方钢管混凝土,D取截面的外表面边长,σc取混凝土的标准抗压强度,p= 2tfy/3D.
基于纤维梁单元模拟核心混凝土的本构模型与实体单元的不同之处在于峰值应力所对应的点是不同的,采用如下混凝土的受压应力-应变关系模型,受压应力-应变曲线同样为公式3,但公式中y=σ/σcc,σcc为约束混凝土峰值应力,计算公式为:
σcc=1.67D-0.112σc+kp
(6)
2.2 钢材本构关系模型
杆件与实体模型中,钢材的本构模型采用ABAQUS软件中提供同向弹塑性模型,满足Von Mises屈服准则.这种模型多用于模拟金属材料的弹塑性性能.用连接给定数据点的一系列直线来平滑地逼近金属材料的应力-应变关系,该模型采用任意多个点逼近实际的材料行为,因此可十分接近真实的材料行为.塑性数据中将材料的真实屈服应力定义为真实塑性应变的函数[17].斜交网格相贯节点所采用钢材多为高强钢材,因此采用双折线模型,曲线分为弹性段(oa)、强化段(ab),如图4所示,弹性模量取206 GPa,强化段的弹模取0.01Es,弹性阶段泊松比取0.30,Es为钢材的弹性模量.
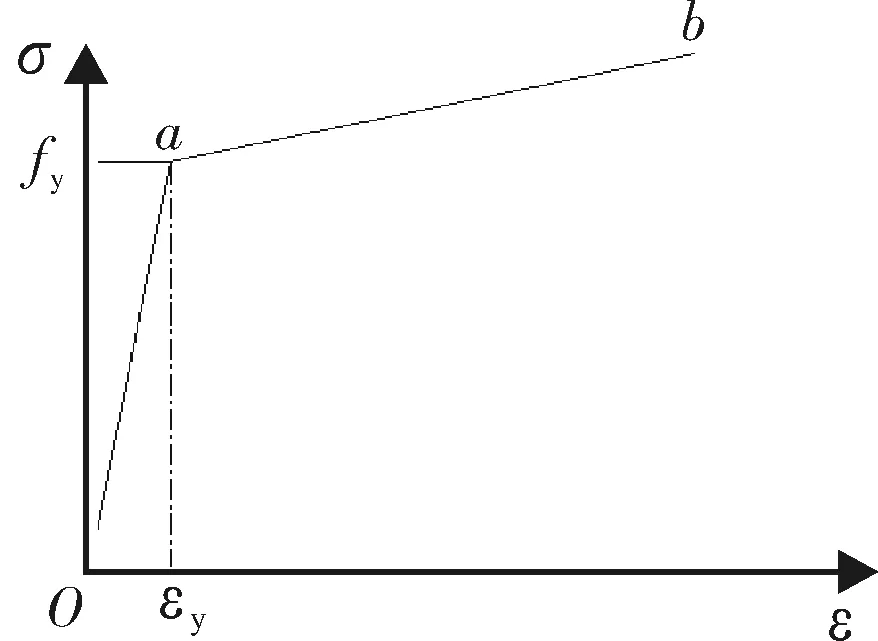
图4 钢材应力-应变曲线Fig.4 Stress-strain curve of steel
3 多尺度有限元模型算例验证取
3.1 圆钢管混凝土节点模型验证
本文以黄超[5]所做实验中的圆钢管混凝土斜交网格相贯节点A-3试验试件为模拟对象,进行轴压荷载作用下的有限元分析.试件A-3设计参数:截面尺寸为 =299 mm×14 mm,杆件端部到中心的长度为1 800 mm,试验测得的钢材屈服强度fy=271.25 MPa,混凝土强度为C60,平面相贯角度35°.为了更好的分析多尺度模型的准确度,分别建立实体模型和多尺度模型.由图5可知,杆件区域约1.2倍的斜柱截面宽度范围内,斜交节点的应力一直处于较高的应力水平,故选取的多尺度耦合界面位置合理,可以较好地掌握节点区的受力情况.而试验结果与两种模型的有限元分析结果荷载-位移曲线对比如图6所示.
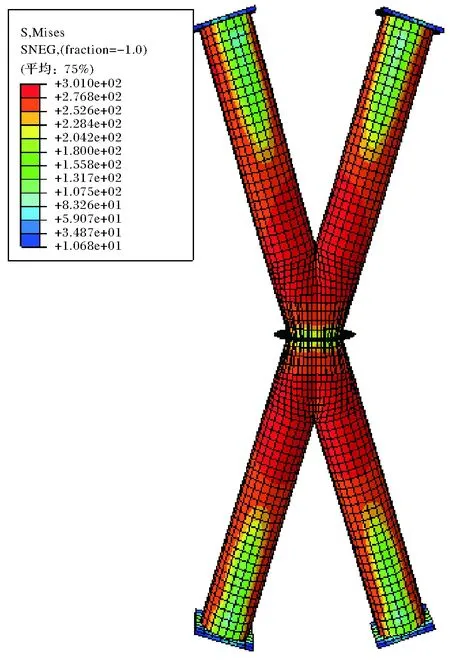
图5 试件A-3 Von mises应力云图Fig.5 Von mises stress nephogram of specimen A-3
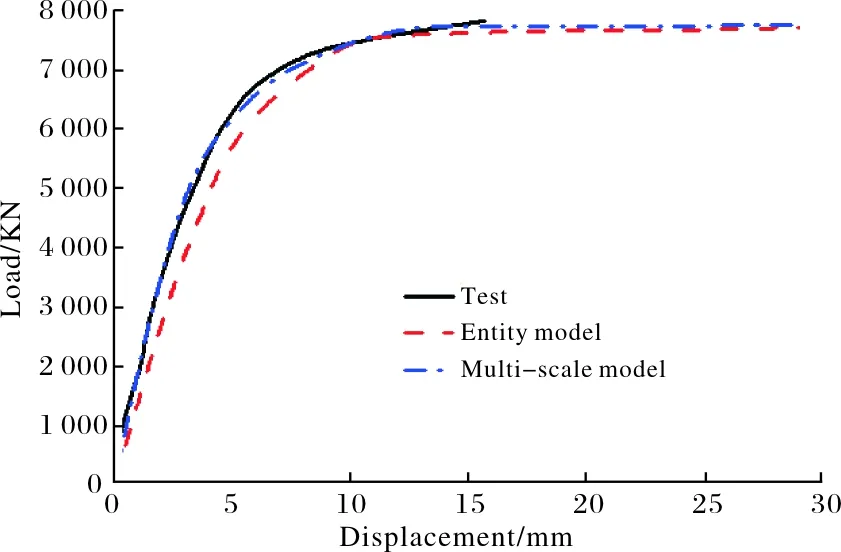
图6 试验结果与计算结果曲线对比Fig.6 Comparison between calculation and test results
由图6可知:(1)多尺度模型计算所得曲线与试验曲线非常接近,无论承载力还是后期的延性性能与试验结果均吻合良好;(2)在弹性阶段,实体模型计算所得曲线与多尺度模型计算所得曲线吻合较差,弹性刚度小于试验值,后期弹塑性阶段曲线吻合较好.总体而言,多尺度有限元模型可以较好地模拟圆钢管混凝土相贯节点在轴向荷载作用下的受压性能.
3.2 方钢管混凝土节点模型验证
目前并没有关于方钢管混凝土相贯节点的试验研究,因此本文以方钢管混凝土相贯节点为模拟对象,建立实体有限元模型与多尺度有限元模型,进行对比分析.试件参数具体如下:方钢管尺寸600 mm×600 mm,壁厚40 mm,杆长3 000 mm,斜柱夹角为35°,钢材Q345,核心混凝土为C40,环向加强版厚度为50 mm,加劲板、竖向连接板和衬板的厚度均为40 mm.两种模型在轴压作用下的荷载-位移曲线对比如图7所示,由图可知:采用多尺度有限元模型计算的曲线与三维实体单元计算曲线吻合较好,界面连接实现了变形协调.
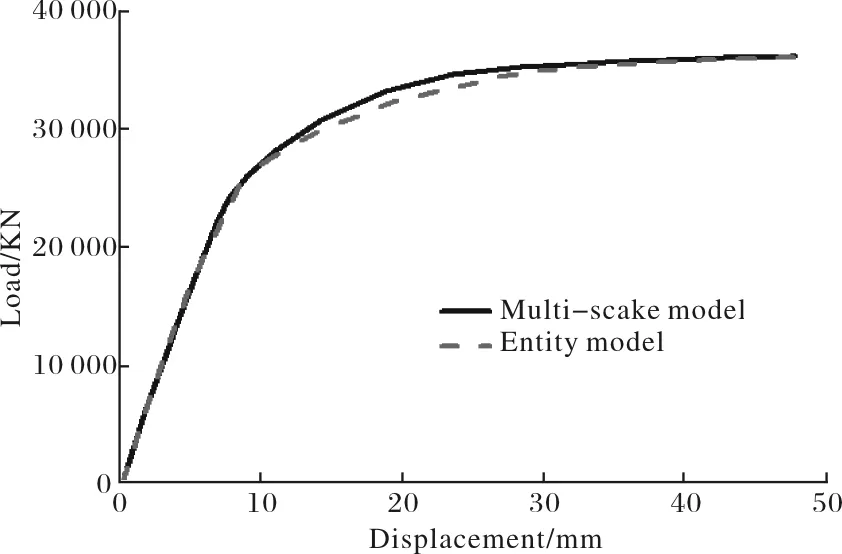
图7 节点的荷载-位移曲线对比Fig.7 Comparison of load-displacement curves of node
另外在计算分析的过程中,得到多尺度模型和实体模型在轴压荷载作用下各构件Von Mises应力云图变化如图8所示,左侧为实体模型,右侧为多尺度模型.由图可知:
(1)两种模型的应力变化分布基本一致,最大应力值出现的位置也相同,多尺度模型耦合界面上不同单元界面上的应力吻合度较高,界面区域未出现不当的应力集中等问题.说明本文建议的界面耦合连接方法可以实现梁单元宏观模型与壳单元和实体单元等细观模型的不同尺度间的过渡,从结构多尺度分析的目的来看,本文的连接方法保证了关键构件或部位的计算精度;
(2)采用同样的计算平台,对比计算时间,多尺度模型计算所用的时间(4 520 s)约为实体模型所用时间(6 740 s)的三分之二.并且达到的计算精度相同,如果应用到高层斜交网格建筑结构计算分析中,会节约更多的时间,节省更多存储.
4 相贯节点性能影响参数分析
本文将相贯角度为35°, 并改变其中某一参数进行单因素有限元数值模拟分析,以此来考察不同参数对方钢管斜交网格相关节点的性能影响.
节点斜交角度α变化时,得到单肢柱的荷载-位移曲线如图9所示.由图可知:(1)随着斜交角度的增大,荷载-位移曲线呈上升趋势,但轴向刚度逐渐减小;(2)斜交角度为40°时,承载力最大,之后随之而减小,这是因为当斜交角度较小时,节点区钢管向外隆起,破坏截面发生在相贯节点区域,随着斜交角度的增大,钢管屈服位置也随之变化,其破坏截面逐渐从节点相贯区域过渡到杆件区域,所以钢管混凝土单肢柱的承载力会下降.从应力云图也可以看出,在相贯角度为60°、90°时破坏截面发生在杆件区域,节点区没有发生破坏,所以其单肢柱的承载力比斜交角度为40°时的承载力低.

图9 不同斜交角度下的荷载-位移曲线Fig.9 Load-displacement curves of different skew angles
钢管厚度、混凝土强度以及钢材强度这三种参数都与约束系数(ξ=Asfs/Acfck)有直接关系,为考察约束系数对节点性能影响,分别对这三种参数进行单因素数值分析,如图10所示.由图可知:当钢管厚度较小或者钢材强度较低或者混凝土强度较高时,荷载-位移曲线有明显的下降段,如AS-10、C80、Q235对应的曲线.主要是由于在这三种情况下核心混凝土受到的约束力小,这三个参数都与钢管混凝土的约束系数有关,此时约束系数ξ<3;当宽厚比为17左右或者混凝土强度为C50左右时,钢管约束作用明显,核心区混凝土受到的约束作用逐渐增大,此时约束系数ξ≈3,荷载-位移曲线大概可分为弹性、弹塑性、塑性三个阶段,如AS-30、C50对应的曲线;而当宽厚比小于17或者混凝土强度低于C50时,计算所得的约束系数ξ>3,此时荷载-位移曲线呈明显的上升趋势,可分为弹性、弹塑性、强化三个阶段,如AS-40、AS-50、C30、C40对应的曲线.通过对比应力云图,发现随着ξ的增大,节点区的屈服范围逐渐向杆件区域扩大,节点区承载力达到极限时,钢管中部向外凸出 ,核心混凝土开始交汇处出现应力集中现象.以上分析结果与钢管混凝土的变形特征基本是一致的.因此,在实际工程中,为了兼顾工程的适用性和经济性,应合理选取节点的约束系数,建议节点危险截面处的约束系数大于3.
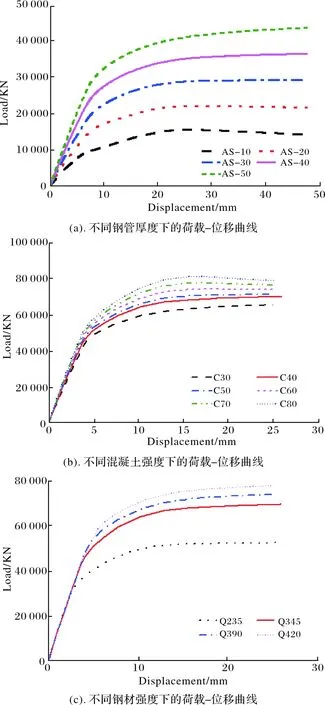
图10 约束系数相关参数对节点的影响Fig.10 The influence of the related parameters of the constraint coefficient
中心连接板厚度与承载力关系如图11所示,发现随着竖向连接板厚度的增加,单肢柱和节点承载力呈现非线性的缓慢增大趋势,当竖向连接板厚度较小时,承载力随连接板厚度的变化有所增大,但当竖向连接板厚度超出2倍钢管壁厚(此处分析为40 mm)时,曲线较为平缓.从变形云图(如图12所示)可以看出,靠近斜柱交汇处的连接板两侧应力较低(轴向应力),端部出现应力集中(环向应力云图),这主要是因为连接板对核心混凝土提供了较高的环向约束应力.这说明竖向连接板在一定程度上可改善相贯节点力学性能,可作为构造措施进行设置,但厚度可适当取小,取值范围为1~2倍钢管壁厚为宜.
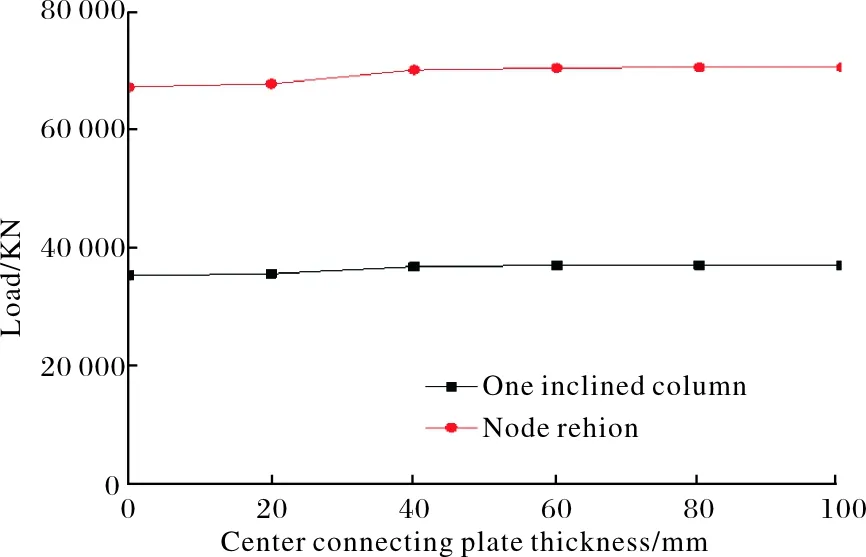
图11 中心连接板与承载力关系图Fig.11 Relationship between center connecting plate and bearing capacity
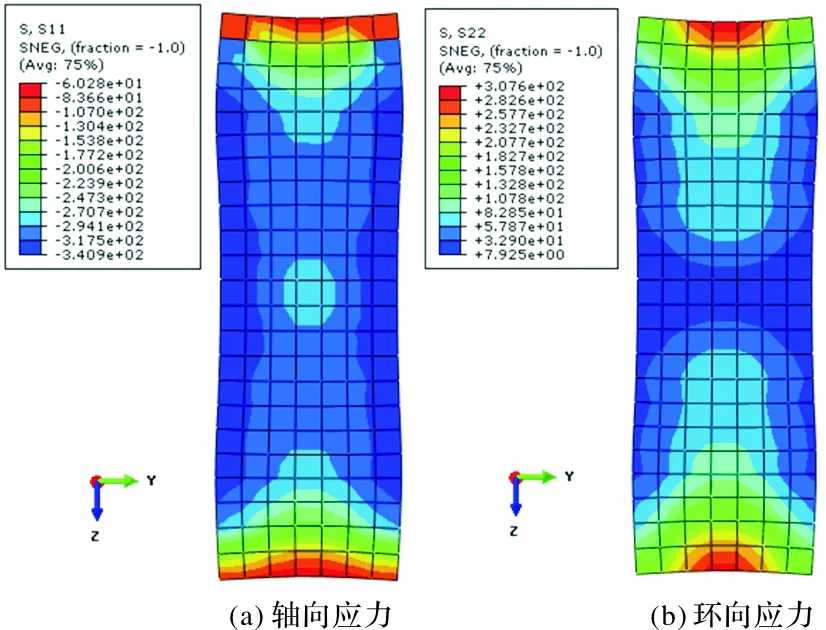
图12 中心连接板的轴向和环向应力云图Fig.12 Axial and circumferential stress nephogram of central connecting plate
通过数值模拟分析发现,衬板厚度的增加对节点承载力的提高不明显.但在同时设置加强环的情况下,加了衬板的相贯节点(A型节点)的屈服范围由节点区域一直延伸到杆件区域,而没有加衬板的相贯节点(B型节点)的屈服范围基本都在节点区域内.由于衬板的作用使节点区域应力最大和首先屈服的位置均发生在其两侧,起到了改善节点区应力集中的作用.如图13所示,有衬板的节点区承载力比无衬板的节点区承载力提高了6%.
通过对von Mises云图分析,发现没有设置加强环板的构件在相贯节点的最小截面处,钢管应力为342.3 MPa,快达到屈服应力345 MPa,而设置了加强环的构件,在相同截面处钢管应力285.2 MPa,没有发生屈服.综上所述,设置环向加强板和衬板是一种必要的构造措施,可以有效改善节点区的延性性能,随着它们的厚度的增加,节点承载力有所提高,但厚度超过1倍钢管厚度时,节点承载力基本无变化.因此,在实际工程中,建议两者厚度均取值为1倍钢管壁厚左右.
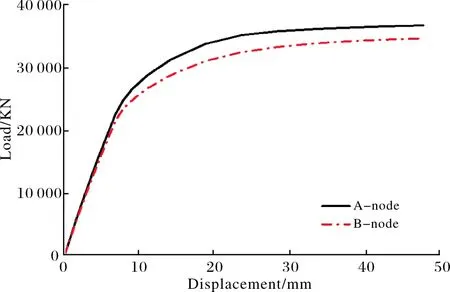
图13 衬板对节点区承载力的影响Fig.13 Influence of lining plate on bearing capacity of joint area
5 结论
本文在已有试验及理论研究的基础上,基于精细单元模型和多尺度模型这两类有限元模型,对方钢管混凝土斜交网格相贯节点在轴压和轴向往复荷载作用下基本力学性能进行有限元分析.可得以下结论:
(1)采用非线性有限元软件对已有试验构件分别建立精细模型和多尺度模型,进行算例验证,与试验结果对比,验证本文多尺度建模方法的正确性.表明本文采用的多尺度建模方法可以运用到钢管混凝土斜交网格相贯节点的研究分析中;
(2)研究结果表明,钢管壁厚、钢材强度、混凝土强度对节点承载力的影响可归结为约束系数ξ的影响,建议在实际工程中ξ取值控制在3.0以上,以保证方钢管混凝土相贯节点的安全可靠;
(3)随着相贯角度的增大,节点区域承载力逐渐增大,但轴向刚度逐渐减小,当相贯角度超过40°时,斜交网格柱的破坏由节点区域转移到杆件区域,构件的承载力由杆件区域承担;中心连接板对相贯节点承载力的提高不明显,可作为构造措施进行设置,建议厚度取值范围为1~2倍钢管壁厚;衬板及环向加强板对相贯节点性能有一定的改善作用,可作为必要的构造措施,建议厚度取值为1倍钢管壁厚.

