A VIEWPOINT TO MEASURE OF NON-COMPACTNESS OF OPERATORS IN BANACH SPACES ∗
Qinrui SHEN (沈钦锐 )
School of Mathematics and Statistics, Minnan Normal University, Zhangzhou 363000, China E-mail: qinrui327@163.com
Abstract This article is committed to deal with measure of non-compactness of operators in Banach spaces. Firstly, the collection C(X) (consisting of all nonempty closed bounded convex sets of a Banach space X endowed with the uaual set addition and scaler multiplication) is a normed semigroup, and the mapping J from C(X) onto F(Ω) is a fully order-preserving positively linear surjective isometry, where is the closed unit ball of X* and F(Ω) the collection of all continuous and w*- lower semicontinuous sublinear functions on X* but restricted to Ω. Furthermore, both are Banach lattices and EK is a lattice ideal of EC. The quotient space EC/EK is an abstract M space, hence,order isometric to a sublattice of C(K)for some compact Haudorspace K,and(FQJ)C which is a closed cone is contained in the positive cone of C(K), where Q: EC→EC/EK is the quotient mapping and F: EC/EK→C(K) is a corresponding order isometry. Finally, the representation of the measure of non-compactness of operators is given: Let BX be the closed unit ball of a Banach space X, then
Key words Measure of non-compactness; measure of non-compactness of operators; Banach lattice; Banach space
1 Introduction
The measure of non-compactness was first proposed by K.Kuratowski[1]in 1930,and later called the measure of set non-compactness or the measure of Kuratowski non-compactness(denoted as α): Let X be a metric space and Q be a nonempty bounded set in X, then,

Let diam(Q)=sup{d(x,y)|x,y ∈Q}, obviously, we have α(Q)≤diam (Q). α can be used to measure the distance between the nonempty bounded set and the compact set in a metric space X, and it has the following properties (where A,B represent any nonempty bounded set in X):
a) α(A)=0 ⇐⇒A is a relatively compact set;
c) A ⊂B =⇒α(A)≤α(B);
d) α(A ∪B)=max{α(A), α(B)};
Furthermore, when X is a normed space, α also satisfies the following properties:
e) α(kA)=|k|α(A), kA={x|x=ka,a ∈A}, k ∈F;
f) α(A+B)≤α(A)+α(B), A+B ={x=a+b, a ∈A, b ∈B};
g) α(coA)=α(A);
h) α(A+x0)=α(A), ∀x0∈X.
In addition, α also has a continuity, that is, for any nonempty bounded set A, B in X, for any ε > 0, there is δ > 0, |α(A)−α(B)| < ε when ρ(A,B) < δ. These properties of α are almost parallel from the properties of the diameter.
In 1957, Goldenstein, Gohberg, and Markus [2] introduced the Hausdorff measure of noncompactness β (also known as the ball measure of noncompactness): Let X be a real Banach space, and Q be a nonempty bounded set in X, then we have

It is equivalent to

or

where K is a compact set in X.
Later, Goldenstein, Gohberg and Markus [3], Sadovskil [4], Goebel [5], and so on, further studied the Hausdorff measure of noncompactness, and proved that β also satisfies the above properties a)–h).
In 1955, Darbo defined Darbo function T for the first time by using the set measure of noncompactness α, and proved that every continuous self mapping T on a bounded closed convex set has a fixed point. The fixed point theorem of Darbo is an important extension of Banach fixed point theorem and Schauder fixed point theorem. The measure of noncompactness of operators was widely used in fixed point, differential equation, integral equation and so on[6,7];In the application of fractional partial differential equations,see[8];The characterizations of compact operators in Banach spaces were given by [9, 10], therefore, it is very important to study the ball measure of non-compactness of operators in Banach spaces.
Mathematicians had defined various kinds of measures of noncompactness in their respective research fields, and some of these measures of non-compactness were essentially the same, and some of these measures had same properties. Mathematicians chose different properties, and resulted in many different axiomatic definitions of measures of noncompactness. At present,the axiomatic definitions of J. Bana´s [11] are the most widely used in the various axiomatic definitions produced in 1980.
Let X be a Banach space, and B(X) be all nonempty bounded closed set families in X.We define Hausdorff metric in B(X):
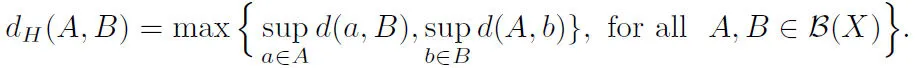
Then, B(X) is a metric space. Let P ⊂2Xis a family, and PCis used to represent the set of closed sets in P.
Definition 1.1([11]) If the family of nonempty set P ⊂N satisfied the following properties:
(2) Ω1∈P and Ω2⊂Ω,Ω2≠∅⇒Ω2∈P;
(3) Ω1,Ω2∈P ⇒λΩ1+(1 −λ)Ω2∈P, for all λ ∈(0,1);
(4) Ω ∈P ⇒coΩ ∈P;
(5) PCis closed in the sense of Hausdorff topology,then P is called a kernel.
Definition 1.2([11]) Let P(X)be a kernel,and if there is a functionµ: B(X)→[0,∞),making kerµ=P, and satisfying the followings:
(A1) µ(Ω)=0 ⇔Ω ∈P(E);
(A3) Ω1⊂Ω2⇒µ(Ω1)≤µ(Ω2);
(A4) µ(coΩ)=µ(Ω);
(A5) µ(tΩ1+(1 −t)Ω2)≤tµ(Ω1)+(1 −t)µ(Ω2), for all t ∈[0,1];
(A6) An∈B(X),=An⊃An+1, for ∀n ∈N,then we called µ a measure of non-compactness with the kernel P. In particular, µ is called a complete measure of non-compactness when P =N .
Furthermore, if µ is completed and satisfied the following properties:
(A7) µ(tA)=|t|µ(A), ∀t ∈R;
(A8) µ(A+B)≤µ(A)+µ(B);
(A9) µ(A ∪B)=max{µ(A), µ(B)},
then µ is said to be a regular measure of non-compactness on the Banach space X.
With the discussion of regular measure of non-compactness in Banach spaces, the above properties (A1)–(A9) are not independent, and Mallet-Nussbaum [12], Cheng-Cheng-Shen-Tu-Zhang [13] gave a more concise definition.
Definition 1.3([13]) Let P(X)be a kernel,and if there is a functionµ: B(X)→[0,∞),making kerµ=P, and satisfying the followings:
(B1) µ(A)=0 ⇔ A is a relatively compact set;
(B2) A ⊂B ⇒µ(A)≤µ(B);
(B3) µ(coA)=µ(A);
(B4) µ(A ∪B)=max{µ(A),µ(B)};
(B5) µ(A+B)≤µ(A)+µ(B);
(B6) µ(tA)=|t|µ(A), ∀t ∈R,
then we call µ a regular measure of non-compactness on Banach space X.
According to the above definitions (B1)+(B4) and(B2)+(B5)+(B6), the following properties (B7) and (B8) can be derived as follows:
(B7) µ(A ∪{x0})=µ(A), x0∈X, A ∈B(X);
In recent years, similar to a regular measure of non-compactness concept, Mallet-Paret and Nussbaum [12, 14] introduced a homogeneous measure of non-compactness: A functionµ: B(X) →[0,∞) satisfying (B1)–(B3) and (B5)–(B8) is called a homogeneous measure of non-compactness on the X.
Kuratowski measure of non-compactness and Hausdorff measure of non-compactness are not only regular measure of non-compactness, but also homogeneous measure of non-compactness.However, the inner Hausdorff measure of non-compactness is not a regular measure of noncompactness, nor a homogeneous measure of non-compactness. It is not difficult to find that every regular measure of non-compactness µ has the following important property:
(B9) If(An)is a decreasing nonempty bounded closed set andis a nonempty compact set.
Similarly, an axiomatic definition of the measure of non-compactness of operators is given.
Definition 1.4Let BXbe the unit ball of a Banach space X,and B(X)is the collection of all bounded linear operators from X to X itself. For every T ∈B(X), if µ is a homogeneous measure of non-compactness, then, µ(T) = µ(TBX) is a homogeneous measure of noncompactness of operator. If µ is a regular measure of non-compactness, then µ(T)= µ(T BX)is a regular measure of non-compactness of operator.
2 Normed Semigroup and Isometric Mapping
The concept of normed semigroup and isometric mapping problems are described in this section. Because all nonempty bounded closed convex sets of a Banach space in the usual sense of addition and multiplication operation are closed, the addition operation also satisfies the commutative law, so all nonempty closed bounded convex sets on a Banach space in addition sense constitute a Abelian semigroup. With the angle of semigroups,we introducted the concept of normed semigroup.
Definition 2.1Let G be a Abel semigroup,F ∈{R,C}. If (x,y)∈(G×G)→x+y ∈G and (α,x)∈(F×G)→αx ∈G, and the following conditions are satisfied for ∀λ, µ∈F and g,g1, g2∈G,

then G is called a module; if we can give a norm in G, then G is called a normed semigroup.
There are many mathematicians studying deeply on normed semigroup, who used to call normed semigroup for space [15], or a compact convex subset of Rnspace [16].
Example 2.2Let X be a Banach space; here are some examples of normed semigroups:
(1) Banach space X itself;
(2) All nonempty convex subsets on X;
(3) All nonempty weakly compact convex subsets on X;
(4) All nonempty super weakly compact convex subsets on X, and the concept of super weakly compact sets are shown in [17–19].
The addition and multiplication of the four classes of sets are given in the usual sense,A1+A2= {a1+a2: a1∈A1,a2∈A2} and λA = {λa : a ∈A}, then they are modules. The Hausdorff metric dHis assigned to the module, and a norm can be induced by the Hausdorff metric:

These four sets were given the norm,constituting a normed semigroup,and are,respectively,called the single point set, compact convex subset, weakly compact convex subset, and super weakly compact convex subset generated by normed semigroup.
Let X be a Banach space,and remember that C(X)(or C)represents the set of all nonempty bounded closed convex sets on X, then we have C(X)⊂B(X),which constitutes a sub-module of addition and multiplication of sets. For ∀A ∈C, define
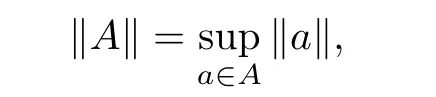

The Hausdorff metric dHis given on C, then

Definition 2.3Let Γ1, Γ2be two poset, and f :Γ1→Γ2, then the followings hold:
(i) We call f be a totally preserving mapping if x ≥y ∈Γ1⇔f(x)≥f(y)∈Γ2;
(ii) When Γ1, Γ2are models, we say that f is positive linear,if for ∀a, b ≥0 and x, y ∈Γ1,satisfying f(ax+by)=af(x)+bf(y).
For every A ⊂X,let σAbe the support function of A,which is restricted on the unit sphere BX∗of the dual space, that is,

Let Ω = BX∗given norm topology, F(Ω) be all continuous and w∗lower semi-continuous sublinear functions on X∗which is restricted on Ω. Because if a bounded continuous function Cb(Ω) with the supremum norm on Ω is a Banach space, then F(Ω) constitutes a closed cone of Cb(Ω).
Structure mapping J: C(X)→F(Ω),

Sets inclusion in normed semigroup C(X) forms a partial order “≥”: A ≥B ⇔A ⊃B.
For mapping J, we have the following lemma.
Lemma 2.4([13]) Let X be a Banach space, then
(i) C(X) is complete with the Hausdorff metric;
(ii) J: C(X)→F(Ω) is a fully order-preserving positively linear surjective isometry, that is, for ∀A, B ∈C(X), then

By a sub-semigroup D(X)(or D) of C(X), unless stated explicitly otherwise, we always mean that it is a normed sub-semigroup and closed under the Hausdorff metric dH. As C(X)is complete (Lemma 2.4), a closed sub-semigroup is always complete.
Theorem 2.5Let A be any bounded set on the normed linear space E, for ∀x ∈E, then

ProofObviously, there isOn the other hand, If y ∈(A),then there are xi∈A, λi≥0 (i=1,2,··· ,n), such that. Because

therefore

thus

Definition 2.6Let X be a Banach space, and D = D(X) be a closed subsemigroup of the normed semigroup C =C(X). D is said to be fundamental if it satisfies the followings:

Lemma 2.7([13]) Suppose that X is a Banach space, and D =D(X) is a subsemigroup of C = C(X). Then, D is closed if and only if every C ∈C satisfying the condition that for∀ε>0, there exists D ∈D(X) and C ⊂D+εBXis in D.
According to Lemma 2.7, we have the following examples of fundamental sub-semigroup of C.
Example 2.8Suppose that X is a Banach space, then we can show that the following are examples of fundamental sub-semigroups of C =C(X):
(a) C itself;
(b) K = K(X), the sub-semigroup of C(X) consisting of all nonempty compact convex sets;
(c) W = W(X), the sub-semigroup consisting of all nonempty weakly compact convex sets.
In fact, it is trivial if D = C. Suppose that D ∈{K,W}, and C ∈C. If it satisfies that for ∀ε > 0, there exists D ∈K (respectively,W) so that C ⊂D+εBX, then we clearly obtain C ∈K (respectively, C ∈W, by Grothendiecks theorem of weak compactness).
3 Generalized Hausdorff Measure of Non-Compactness of Operators
In this section, we define a generalized Hausdorff measure of operators through the fundamental sub-semigroups D of C, by using quotient semigroup JC/JD and quotient norm of quotient space EC/ED, then the representation theorem of this measure of operator is given,where
Definition 3.1A partially ordered real Banach space X is called a Banach lattice provided

If a subspace Y of X satisfies x ∨y ∈Y for every x,y ∈Y, we called Y a sublattice of X.
If a sublattice Y of X satisfies that for every x ∈X, there exists y ∈Y , |x| < |y|, such that x ∈Y, then Y is called a lattice ideal of X.
From (iv) and

we know that the lattice operators are continuous in terms of norm.
In addition to the description, the lattice operator defined in the real valued function space C(K) is as follows: for ∀x,y ∈C(K) and k ∈K, we have

For a given sub-semigroup D ⊂C, let ED=
Lemma 3.2([13]) Let X is a Banach space,then for any sub-semigroup D of C satisfying that ∀C,D ∈D implied co{C ∪D}∈D, the space EDis a Banach lattice.
Using K = K(X) to denote all nonempty compact convex subsets in X, from the above lemma, both EC=and EK=are Banach lattice, and we have the following lemma.
Lemma 3.3([13]) Suppose that X is a Banach space. Then
(i) EKis a lattice ideal of the Banach lattice EC;
(ii) The quotient space EC/EKis an abstract M space, therefore, order isometric to a sublattice of a C(K) space for some compact Hausdorff space K.
(iii) (FQJ)C is a closed cone contained in the positive cone of C(K) , where Q: EC→EC/EKis the quotient mapping and F: EC/EK→C(K) is the corresponding order isometry.
Definition 3.4Let X be a Banach space,and D =D(X)be a fundamental sub-semigroup of the normed semigroup C =C(X). A non-negative-valued functionµD: B(X)→R defined on B(X)is said to be the ball measure of non-property D provided for every nonempty B ∈B(X),
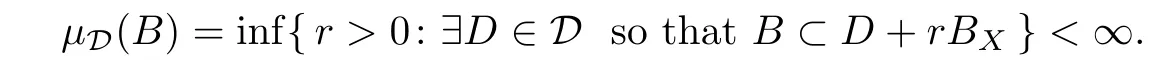
For ∀T ∈B(X),the functionµD(T)=µD(T(BX))is said to be the ball measure of operator of non property D, abbreviated as µ(T).
There are many possibilities, but the followings are main interesting to us:
(1) D =K, in this case, we call µ(T)=β(T) the Hausdorff measure of non-compactnss of operators ;
(2) D = W, in this case, µ(T) = W(T) is said to be the Hausdorff measure of non weak compactness of operators.
Theorem 3.5Let X be an infinite dimensional Banach space, and BXbe the unit ball of X. If, then
(1) µ(BX)=1;
(2) µ(B(A,r))=µ(A)+r.
Proof(1) Obviously, BX⊂{0}+1BX, thus µ(BX) ≤1; On the other hand, letting 0 < µ(BX) = a < 1, by definition, there exists D ∈D, such that BX⊂D + aBX, thenµ(BX)≤µ(D+aBX)=aµ(BX), which is the contradiction between a ≤a2and 0 (2) µ(B(A,r)) =µ(A+rBX)≤µ(A)+rµ(BX)=µ(A)+r; On the other hand, supposeµ(A) = k > 0, then by the definition of µ, there exists AD + (k −δ)BXfor ∀δ > 0 and D ∈D, thus A+rBXD+(k −δ)BX+rBX= D+(k −δ+r)BX, so µ(A+rBX) ≥µ(D+(k−δ+r)BX)=k+r−δ. The arbitrariness of δ consists ofµ(A+rBX)≥k+r =µ(A)+r. For a closed normed sub-semigroup D contained in C, let C/D be the quotient normed semigroup, that is, for=C+D, the induced quotient normis defined by Theorem 3.6Given a closed normed sub-semigroup D of C,let the quotient normbe defined by the previous definition. We denote by µ(T) the ball measure of operators of non property D. Then, for every T ∈B(X), we obtain ProofFor BX∈B, lettingand supposing µ(T(BX)) = α > 0, then there exists D ∈D such that C ⊂D+(α+ε)BXfor every ε>0. Therefore, Then, With the arbitrariness of ε, we have On the other hand, it follows from definition ofand Lemma 2.4 that for all ε>0, there exists D ∈D such that then or, equivalently, As ε is arbitrary, we have Given a Banach space X,and a sub-semigroup D of C(X),we useto denote the quotient norm of the quotient space Cb(Ω)/EDand Q: Cb(Ω) →Cb(Ω)/EDis the quotient mapping.For every T ∈B(X,X), we also have the following norm representation of the measure µDof non property D. Theorem 3.7Let X be a Banach space, and BXbe the unit ball on X. For ∀T ∈B(X,X), let D be a fundamental sub-semigroup of C(X), then we have ProofFor BX∈B, assume that, then By Theorem 3.6, we have On the other hand, as JD −JD is dense in ED, for every ε > 0, there exists D, E ∈D such that According to Lemma 2.4 and Theorem 3.6, we have As E ∈D, we get Thus, As ε is arbitrary,we obtain From the above representation theorem, the ball measure of operators of non property D has the following properties. Theorem 3.8Suppose that X is a Banach space and BXis the unit ball on X, then for∀T,T1,T2∈B(X),a fundamental sub-semigroup D of C(X)(particularly,D ∈{K, W}),µ(T)satisfies the following properties: Proof(1) Suppose∈D, and by definition and Theorem 3.7, there is obviouslyµ(T)=0. Conversely, for all ε>0, there exists σC−σD∈JD −JD, such that which is equivalent to then thus As C −D ∈D and D is fundamental, then If D =K , obviously there exists T ∈K(X,X); if D =W, we get T ∈W(X,X). (2) It can be proved as follows: (3) For all k ≥0, we have So for all k ∈R, we obtain (4) The conclusion is obviously. (5) Let y =TBX,then ∃x ∈BX,y =Tx,such that,so According to Theorem 3.5 and Theorem 3.7, we have (6) Supposing that µ(T2)=µ(T2BX)=a, there exists a finite set A such that therefore,
























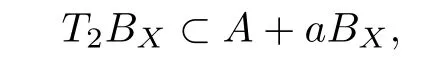

 Acta Mathematica Scientia(English Series)2020年3期
Acta Mathematica Scientia(English Series)2020年3期
- Acta Mathematica Scientia(English Series)的其它文章
- MINIMAL PERIOD SYMMETRIC SOLUTIONS FOR SOME HAMILTONIAN SYSTEMS VIA THE NEHARI MANIFOLD METHOD∗
- TOEPLITZ OPERATORS WITH POSITIVE OPERATOR-VALUED SYMBOLS ON VECTOR-VALUED GENERALIZED FOCK SPACES ∗
- LIE-TROTTER FORMULA FOR THE HADAMARD PRODUCT *
- AN ABLOWITZ-LADIK INTEGRABLE LATTICE HIERARCHY WITH MULTIPLE POTENTIALS *
- MULTIPLICITY OF POSITIVE SOLUTIONS FOR A NONLOCAL ELLIPTIC PROBLEM INVOLVING CRITICAL SOBOLEV-HARDY EXPONENTS AND CONCAVE-CONVEX NONLINEARITIES *
- ASYMPTOTIC CONVERGENCE OF A GENERALIZED NON-NEWTONIAN FLUID WITH TRESCA BOUNDARY CONDITIONS∗
