基于隐马尔科夫模型的变压器剩余寿命分析*

陈长征， 刘 洋

(沈阳工业大学 机械工程学院， 沈阳 110870)

区别于传统变压器运维的定期维修方式，基于全寿命周期管理技术的视情维修机制将成为变压器运营和维护的发展趋势.目前为止，全寿命周期技术也仅应用于例如美军战机F-35、美军装备的直升机健康与使用监测系统(HUMS)[1]等耗资巨大且安全系数极高的军用领域.Banjevic等[2]提出可靠度函数及剩余寿命函数计算方法；郝会兵[3]根据冲击理论等方法和马尔科夫链蒙特卡洛建立基于性能退化数据的可靠性分析模型；伍建军等[4]提出了一种小波技术与SVR融合的RUL预测方法解决在非线性、非平稳部分可观测状态下破碎机辊套RUL难以准确预测的问题；尚永爽等[5]利用隐马尔科夫模型对飞机陀螺仪进行剩余寿命预测；王航等[6]采用Cox比例风险模型，定量分析了电缆故障影响因素，运用Logistic回归模型确定了电缆故障影响因素类别；Sun等[7]采用概率分布函数和累积分布函数来量化预测的不确定性，建立了基于刀具磨损历史数据的非线性刀具剩余寿命预测模型.

基于以上理论研究，本文提出一种基于隐马尔科夫模型[8]的电力变压器剩余寿命(RUL)预测方法，利用系统已退化数据以及已知历史退化数据对变压器系统剩余寿命做出预测[9]，为变压器系统寿命视情维修提供可靠依据.

1 系统剩余寿命模型建立

比例故障模型又称为Cox模型[10-11]，是一种有关装备检测数据以及历史寿命等寿命数据的统计分析方法，表示系统运行时间小于运行时间t的比率，基本形式为

λ(t，Zk)=λ0(t)eδZk

(1)

式中：λ(t，Zk)为故障率；Zk为协变量，即系统运行监测值协方差；λ0(t)为与时间相关的故障率；δ为回归参数，表示协变量对故障函数的影响系数.假设各参数的数值不随时间变化而变化.

1.1 完全信息条件下系统剩余寿命模型建立

故障比例函数(1)服从三参数威布尔分布，可表示为

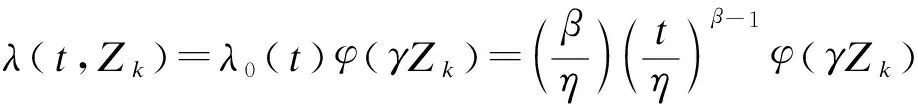
(2)

式中：η、β、γ分别为尺度参数、形状参数、位置参数；尺度参数η表示故障寿命均值分布中点的大致位置；位置参数γ代表了伴随变量Zk对故障率的影响，在γ之前故障不会发生，故γ也被称为最小寿命，当γ较小时其伴随变量对故障率影响较小，可忽略；φ(γZk)为变压器退化函数；形状参数β表示系统老化退化特性，其取值β>1，故障率随时间是增加的.对威布尔分布的三个参数β、η、γ进行参数估计，可确定变压器退化函数，从而开展状态评估及寿命预测.

文献[12]提出的可靠度函数为

R(k，Zk，t)=P(T>kΔ+tT>kΔ，Z1，Z2，…，Zk)=

P(T>kΔ+tT>kΔ，Zk)=

(0≤t≤Δ)

(3)

式中：条件可靠度函数R()表示已知变压器系统在Δ，2Δ，…，kΔ时刻的状态分别为Z1，Z2，…，Zk，在kΔ时刻没有发生故障，继续工作到kΔ+t时刻的概率；T为变压器发生故障的运行时间.假设运行时系统退化参数维持定值，在下一监测点之前状态转移矩阵发生变化，即状态变化时间不超过Δ.

由此推出，若在kΔ时刻系统状态为Zk且继续不做任何维护方式继续运行，在t时间内剩余使用寿命为

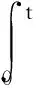
(4)

在t>Δ的一般情况下，在监测点后任意时刻系统状态都可能发生变化，上述模型并不适合，故需将数学模型推广到更一般情况.在监测点k时，系统状态Zk条件下，由式(3)根据贝叶斯公式类比出在t>Δ条件下可靠度函数为

R(k，Zk，t)=P(T>kΔ+tT>kΔ，Z1，Z2，…，Zk)=

P(T>kΔ+tT>kΔ，Zk) (t>Δ)

(5)

在t>Δ条件下，变压器系统由状态Zk运行t时间，根据贝叶斯公式可得仍未发生故障的概率为P(T>(k+1)ΔT>kΔ，Zk)=R(k，Zk，Δ)，在(k+1)Δ时刻前状态由Zk转变为Zk+1，在Zk+1状态下变压器继续工作时长为t-Δ，即在(k+1)Δ时刻后的工作时长，概率为P(T>kΔ+tT>(k+1)Δ).可以得出在状态Zk下，运行t时间的可靠度函数为

tT>(k+1)Δ，Zk+1=j)=

tT>(k+1)Δ，Zk+1=j) (t>Δ)

(6)

式中，P(T>kΔ+tT>(k+1)Δ，Zk+1=j)为在k+1监测点状态为j时工作到时间kΔ+t的概率，根据可靠度函数可表示为R(k+1，j，t-Δ).代入式(6)，并将式(3)整理得到在完全信息条件下变压器系统运行可靠度函数为

(7)

由此，文献[2]给出了完全信息条件下，系统运行的剩余寿命(RUL)函数为

e(k，i)=E(T-kΔT>kΔ，Zk=i)=

(8)

1.2 部分信息条件下变压器剩余寿命模型建立

上文所述为理想状态下变压器系统运行时系统状态，但实际运行中变压器系统难免受到例如风扰和噪声等因素影响.在信号采集时也会存在某种程度的检测误差、采集信息丢失，故在实际运行情况下无法获得变压器系统精准运行状态，进而需要建立一种方式表示变压器系统状态空间.

对于监测点k+1，根据采样空间θ∈Θ，利用贝叶斯公式将监测点k条件概率分布ck更新为ck+1，其表达式为

(9)

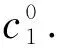
(10)

故在部分隐含参数未知条件下，监测点k处当系统状态空间条件概率分布为ck时，变压器剩余寿命为

(11)

2 剩余寿命模型算法应用

以东北地区某换流站直流换流变压器为计算验证对象，部分监测点如图1所示.图2为监测模块.

图1 变压器监测现场Fig.1 Transformer monitoring site

根据变压器退化影响主要参数，选取系统运行机械振动频率、机械振动幅值、外部温度、内部油温、工作频率、空载损耗(铁损)、短路损耗(铜损)、阻抗等八项性能指标作为计算值，监测值如表1所示.

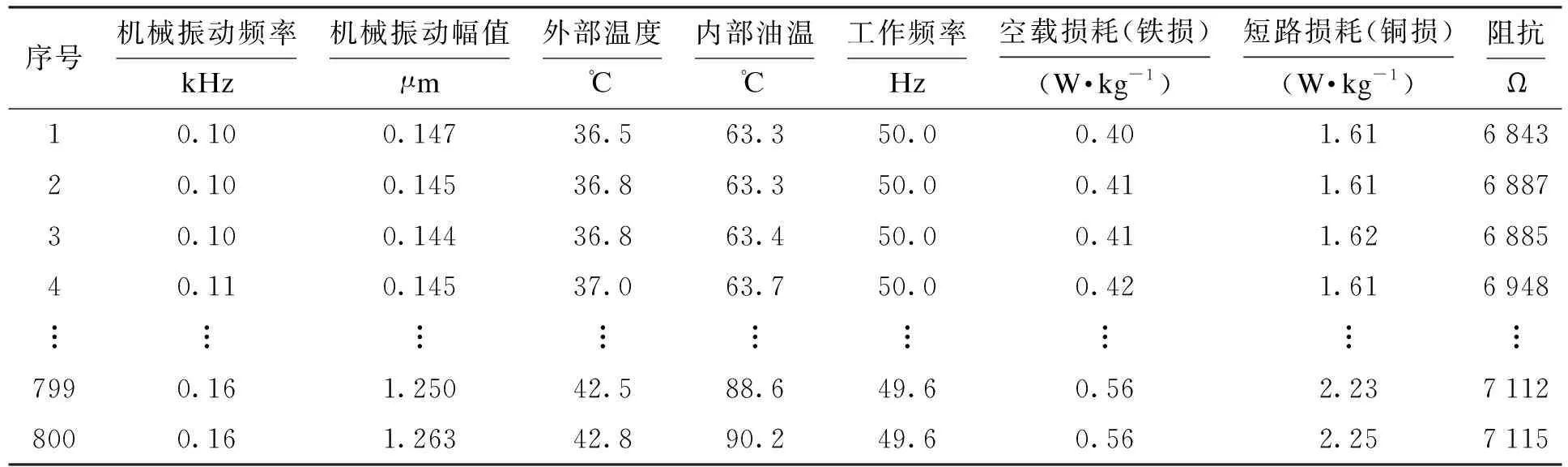
表1 ±500 kV直流换流变压器性能参数Tab.1 Performance parameters of ±500 kV DC converter transformer

变压器故障模型由两参数威布尔分布可得

(12)

设定初始参数η=820，β=1.4，则有

φ(γZk)=exp(0.1(Zk-1))

根据变压器实际运行情况，选取检测时间间隔Δ=750，根据式(1)、(2)得到系统故障率函数、系统可靠度函数为

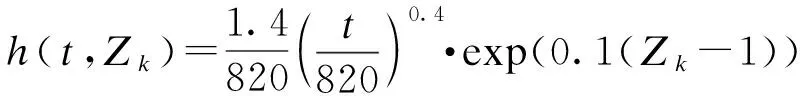
(13)

(14)

根据系统可能存在状态，设初始条件下概率分布c0={1，0，0}，根据故障概率模型计算状态转移矩阵，即

观测值θ有3个取值，故将变压器运行状态与观测概率Q建立以下关系：

假设以上为状态模型完全信息状态下，在Δ=750时，不同监测点k=1，2，…，53由式(8)得到剩余寿命，结果如表2所示.在k=0时，变压器处于全新状态，状态2、3不存在，状态1时该变压器剩余寿命为39 750.3 h.

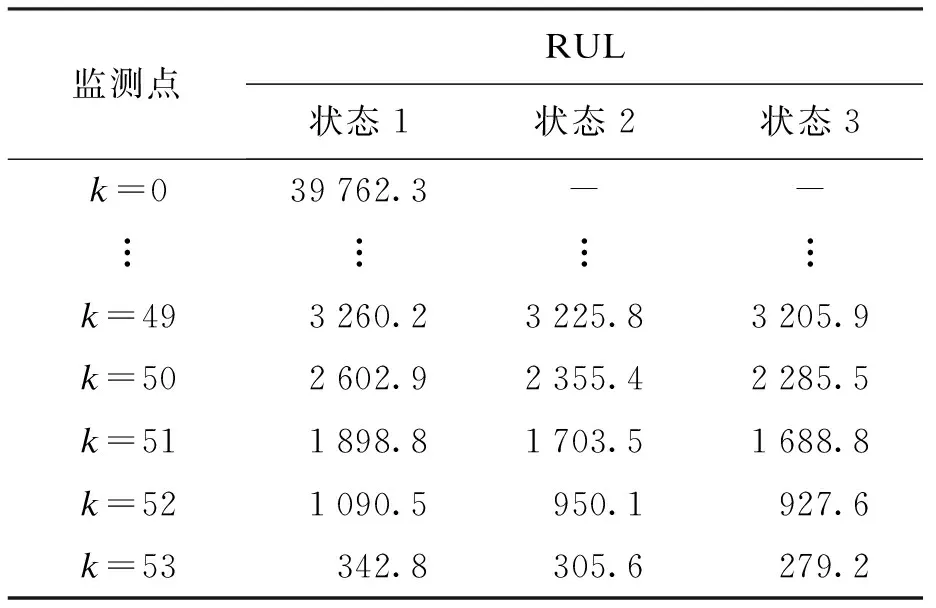
表2 完全信息下变压器各监测点剩余寿命Tab.2 RUL of each monitoring point of transformer with complete information h

真实情况下，变压器系统所采集数据类型为部分不可观测，由式(9)～(11)计算剩余寿命，预测剩余寿命数据与完全信息条件下剩余寿命对比如图3所示，两种条件下剩余寿命预测相对误差对比如图4所示.设在监测点k=49，50，51，52，53处，观测值分别取值1，1，2，3，3，将预测寿命部分信息条件下变压器预测寿命放入表3进行对比.

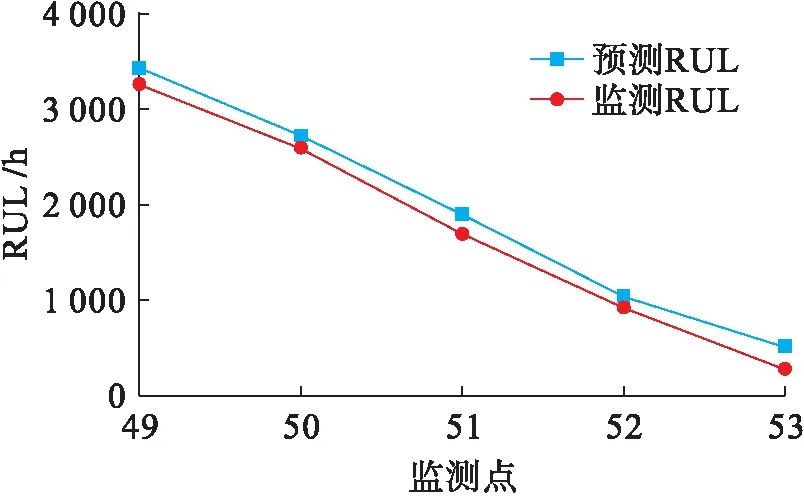
图3 全部与部分信息条件下变压器剩余寿命对比Fig.3 Comparison of transformer RUL under complete and partial information conditions

图4 两种条件下剩余寿命预测相对误差对比Fig.4 Comparison of relative errors of RUL prediction under two conditions

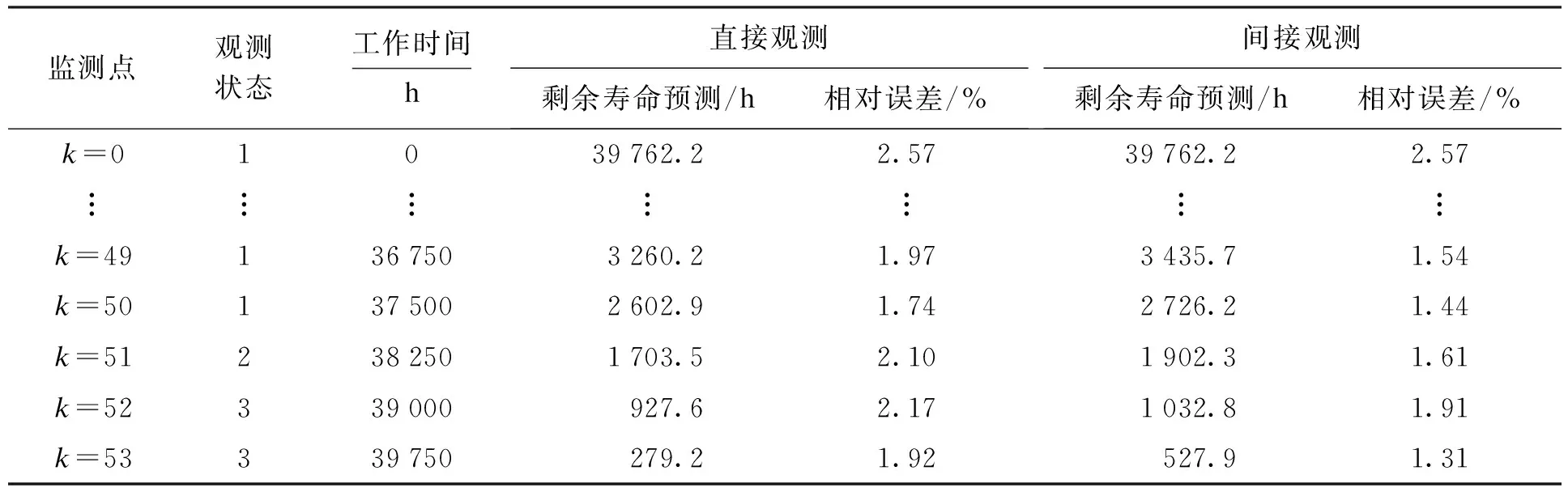
表3 完全信息条件与部分可观测条件下剩余寿命预测对比Tab.3 Comparison of RUL prediction under complete information and partially observable conditions

根据实际历史寿命数据，将相关数据代入上述算法，得出被检测的±500 kV换流变数据模型故障时间为40 812.2 h，表3给出了两种数学模型的预测对比.

根据表3的对比可以得出，剩余寿命在部分可观测条件下的预测值明显优于完全信息条件下的剩余寿命预测值，具有更高的准确度.

3 结 论

本文综合利用历史故障数据基于部分可观测模型的变压器系统剩余寿命预测计算模型.通过具体算例验证，在不完全信息条件下剩余寿命预测模型准确率要高于传统完全信息条件下模型准确率，对变压器系统视情维修提供参考依据，但模型参数的选择及工程适用程度有待进一步提高.