Wind-forced equatorial wave dynamics of the Pacifi c Ocean during 2014/2015 and 2015/2016 El Niño events*
WANG Jing , , YUAN Dongliang , XU Tengfei , ZHAO Xia ,
1 CAS Key Laboratory of Ocean Circulation and Waves, Institute of Oceanology, Chinese Academy of Sciences, Qingdao 266071, China
2 Pilot National Laboratory for Marine Science and Technology (Qingdao), Qingdao 266071, China
3 Center for Ocean Mega-Science, Chinese Academy of Sciences, Qingdao 266071, China
4 First Institute of Oceanography, Ministry of Natural Resources, Qingdao 266061, China
Abstract The equatorial wave dynamics of interannual sea level variations between 2014/2015 and 2015/2016 El Niño events are compared using the Laboratory of Numerical Modeling for Atmospheric Sciences and Geophysical Fluid Dynamics, Institute of Atmospheric Physics Climate Ocean Model (LICOM) forced by the National Centers for Environmental Prediction (NCEP) reanalysis I wind stress and heat flux during 2000–2015. In addition, the LICOM can reproduce the interannual variability of sea surface temperature anomalies (SSTA) and sea level anomalies (SLA) along the equator over the Pacifi c Ocean in comparison with the Hadley center and altimetric data well. We extracted the equatorial wave coefficients of LICOM simulation to get the contribution to SLA by multiplying the meridional wave structure. During 2014/2015 El Niño event, upwelling equatorial Kelvin waves from the western boundary in April 2014 reach the eastern Pacifi c Ocean, which weakened SLA in the eastern Pacifi c Ocean. However, no upwelling equatorial Kelvin waves from the western boundary of the Pacifi c Ocean could reach the eastern boundary during the 2015/2016 El Niño event. Linear wave model results also demonstrate that upwelling equatorial Kelvin waves in both 2014/2015 and 2015/2016 from the western boundary can reach the eastern boundary. However, the contribution from stronger westerly anomalies forced downwelling equatorial Kelvin waves overwhelmed that from the upwelling equatorial Kelvin waves from the western boundary in 2015. Therefore, the western boundary reflection and weak westerly wind burst inhibited the growth of the 2014/2015 El Niño event. The disclosed equatorial wave dynamics are important to the simulation and prediction of ENSO events in future studies.
Keyword: Pacifi c Ocean; equatorial waves; western boundary reflection; El Niño
1 INTRODUCTION

Fig.1 Comparison of simulated monthly SSTA time series (thick dash) in the Niño 3 region with the OISST data (shading) 2000–2015
El Niño and La Niña events are the strongest anomalous climate events in the tropical Pacifi c Ocean. El Niño (La Niña) events are warm (cold) phases of the Pacifi c El Niño-Southern Oscillation (ENSO), which have global repercussions even influences in the Indian Ocean. Figure 1 shows the Niño 3 index (shading) since 2000 using Optimum Interpolation Sea Surface Temperature (OISST) data based on the period of 1982–2015. The anomaly is calculated relative to a monthly climatological seasonal cycle based on the years 1982–2005. Strong El Niño events have been identifi ed by the commonly used defi nitions in years 1982/1983, 1986/1987, 1997/1998, 2002/2003, 2004/2005, 2006/2007, 2009/2010, 2015/2016 (Santoso et al., 2017). The Scientifi c community was abuzz that a strong El Niño event did not evolve in 2014 despite westerly wind bursts (WWBs) occurred west of the dateline in early 2014 (Menkes et al, 2014; McPhaden, 2015). In the conventional description of ENSO, WWBs trigger an El Niño event with multiple WWBs initiating the largest El Niño events (McPhaden, 1999; Yu et al., 2013). Wind stress anomalies determine the magnitude and timing of El Niño events (Penland and Sardeshmukh, 1995; Penland, 1996). Westerly anomalies forced downwelling equatorial Kelvin waves play an important role in the coupled process of the equatorial Pacifi c Ocean and the atmospheric condition associated with ENSO (Lengaigne et al., 2004). The latest studies have demonstrated easterly wind bursts in the boreal summer inhibit the development of an El Niño event (Menkes et al., 2014; Hu and Fedorov, 2016) and also push the 2015–2016 El Niño to an extreme event (Levine and McPhaden, 2016). The development of the 2014/2015 and 2015/2016 El Niño events forms an important comparison in ENSO dynamics, which has drawn widespread attention recently. Equatorial waves play an important role in the conceptual ENSO oscillators including the delayed oscillator (Schopf and Suarez, 1988; Battisti and Hirst, 1989), advective-reflective oscillator (Picaut et al., 1997) and Western Pacifi c oscillator (Weisberg and Wang, 1997). However, the role of equatorial wave dynamics during the 2014/2015 and 2015/2016 El Niño events has not been studied before. We will use the 2014/2015 El Niño for convenience in the following text although the 2014 El Niño did not evolve to a strong event.
Both Western boundary and eastern boundary reflections play an important role in ENSO cycles in the Pacifi c Ocean (Gent and Luyten, 1985; Rothstein et al., 1985; Schopf and Suarez, 1988; Kessler and McCreary, 1993) and even in the evolution of the Indian Ocean Dipole in the Indian Ocean (Yuan and Liu, 2009; Wang and Yuan, 2015). There are still uncertainties about the wind-forced and westernboundary-forced equatorial Kelvin waves from the western Pacifi c Ocean (Boulanger and Menkes, 1999; Delcroix et al., 2000) associated with the approximation made to derive the wave coefficients from altimetry. Some studies ignore the nonlinearities using the linear model of the interannual equatorial waves (McPhaden and Yu, 1999; Delcroix et al., 2000). Yuan et al. (2004) studied the dynamics of ENSO oscillator paradigm in the 1990s using improved wave decomposition method and nonlinear general ocean circulation model (OGCM). However, a tropical Pacifi c Ocean model with closed western boundary and lateral boundaries is used in their study. Therefore, the process of the western boundary reflection in the Pacifi c-only OGCM is not realistic. In our study, a nonlinear quasi-global model with real topographic boundary and complete dynamics of the ocean circulation is used to study the equatorial wave dynamics during 2014/2015 and 2015/2016 El Niño events. Therefore, the analyses of equatorial waves based on the nonlinear OGCM are likely reliable in the Pacifi c Ocean.
In this paper, we offer a possible explanation for why the 2014/2015 El Niño event did not evolve a strong ENSO event by using a nonlinear OGCM and by focusing on equatorial wave dynamics in comparison with the 2015/2016 El Niño event. In Section 2, we give a description of the data and model, and then present the model results and wave analyses for the evolution of two El Niño events in Section 3. At last, discussion and conclusions are presented in Section 4 and Section 5, respectively.
2 DATA AND METHOD
The Niño 3 index data are from the OISST weekly data based on the period 1982–2019. The data can be downloaded from the following website: http://stateoftheocean.osmc.noaa.gov/sur/pac/. World Ocean Atlas 2013 version 2 (WOA13) data are used to validate the model simulated vertical profi les of density and buoyancy frequency. The WOA13 data consist of a set of objectively analyzed climatological fi elds of in situ temperature and salinity etc. (Boyer et al., 2013). The annual mean density and buoyancy frequency squared are calculated based on WOA13 data. The sea surface temperature (SST) data from the Hadley Center data (HadISST, Rayner et al., 2003) are used to validate the simulated SST. The SST climatology was computed based on the monthly average SST data during 2000–2015. Basic data sets and procedures are described in Kessler (1990) and Kessler and McCreary (1993). The monthly sea level anomalies (SLA) from the Archiving, Validation, and Interpretation of Satellite Oceanographic (AVISO) data with a horizontal resolution of 0.25° longitude by 0.25° latitude from 2000 to 2015 are used in this study. The domain covers the region of (0.125°–359.875°, 89.875°S–89.875°N). The daily forcing of wind stress and heat flux from National Centers for Environmental Prediction (NCEP) reanalysis I data is used as the forcing of the OGCM with horizontal resolution of 2.5°×2.5° from 1948 to 2015.
The OGCM used here is the LICOM (LASG/IAP Climate Ocean Model, version 1.1) developed from Laboratory of Numerical Modeling for Atmospheric Sciences and Geophysical Fluid Dynamics, Institute of Atmospheric Physics (LASG/IAP). The model has a free sea surface and nearly leveled vertical coordinates in the deep ocean. There are total 30 levels in the vertical with 12 layers in the upper 300 m. And their depths locate at around -12.5, -37.5, -62.5, -87.5, -112.5, -137.5, -162.5, -187.5, -212.5, -237.5, -262.5, -287.5, -313.5, -344.6, -387.8, -450.7, -540.3, -662.8, -823.6, -1 026.6, -1 274.6, -1 569.0, -1 909.9, -2 295.8, -2 724.0, -3 190.3, -3 689.6, -4 215.6, -4 761.3, and -5 319.1 m. The model domain covers quasi-global ocean (0°–360°, 78.5°S–90°N) with a horizontal resolution of 0.5° longitude by 0.5° latitude. The enhancing mixing in the surface layer follows the mixing scheme used in the paper of Pacanowski and Philander (1981). The model has been spun up for 900 years using climatological forcing of Levitus data from the rest (Levitus and Boyer, 1994). More details of LICOM confi guration have been described in Liu et al. (2004a, b). A control run is conducted using the daily forcing of wind stress and heat flux from NCEP reanalysis I data from 1948 to 2015. Sea surface temperature and salinity are relaxed to the Levitus climatology data at a time scale of a half-year (Levitus et al., 1998). The analysis of this paper is based on monthly averaged output of the LICOM simulation from 2000–2015. In this study, we also presented the 1997/1998 El Niño event in comparison with the 2014/2015 and 2015/2016 El Niño events in the discussion section. Here, the climatology is calculated based on the monthly averaged output of the LICOM simulation from 1990–2001.
Based on the orthogonal relations of the long equatorial Kelvin and Rossby mode functions, the pressure and zonal currents are projected onto the vertical modes to extract the vertical mode amplitudes, which can be decomposed into the meridional modes. The projection includes the nonlinear effects of the LICOM simulation in the calculation of equatorial wave coefficients by treating the nonlinear terms of the LICOM momentum equations as forcing terms. The pressure and zonal current anomalies from LICOM simulation are decomposed into equatorial waves based on the theory of linear equatorial waves (McCreary, 1981). The Kelvin wave speed was 2.71 m/s for the fi rst baroclinic mode based on the WOA13 data, which is consistent with the calculation of Chelton et al. (1998). The wave decomposition method used here is the same as the method in appendix A in the paper of Yuan et al. (2004).
In order to disentangle the contribution of the wind-forced and reflected wave contribution, we used a simple linear Kelvin wave characteristic-line model to quantify their relative roles. The zonal wind stress anomalies from NCEP reanalysis I data is projected onto equatorial Kelvin and Rossby wave modes then is integrated along the characteristic lines with zero condition at the western boundary in the Pacifi c Ocean for wave solutions. Linear wave model has been introduced in previous studies (Yuan and Han, 2006; Wang and Yuan, 2015). The linear wave model results could estimate the relative contribution of the reflections and wind forcing to the equatorial wave coefficients. In the OGCM output, the contributions from the western boundary reflections and wind forcing cannot be separated quantitatively. The monthly mean zonal wind stress from the NCEP reanalysis I daily wind stress data is projected onto the equatorial Kelvin wave and Rossby wave modes, then is integrated along the characteristic lines of equatorial Kelvin waves to obtain the wave coefficients. The eigenvalues and eigen-functions are calculated from the mean vertical profi les of density over the equatorial Pacifi c Ocean between 5°S and 5°N using WOA13 data. In this paper, we artifi cially choose the 151°E as the western boundary in the Pacifi c Ocean since the western boundary reflection is very complicated with one or more narrow gaps at the western boundary (Spall and Pedlosky, 2005).
3 RESULT
In this section, the interannual variability of SLA and SST anomalies simulated by LICOM is validated with the AVISO altimeter SLA data and Hadley Center data, respectively. In addition, the equatorial wave coefficients are extracted from LICOM simulation to analyze the influence of the propagation and reflections of equatorial waves on the evolution of the El Niño events during 2014–2015 and compared to the solution of linear wave model.

Fig.2 Time-longitude plots of monthly SST anomalies from Hadley centre data (a) and the LICOM simulation (b); averaged between 5°S–5°N along the equator during 2000–2015 (unit: °C)
3.1 Model validation
El Niño events occurred during the years 2002/2003, 2004/2005, 2006/2007, 2009/2010, and 2015/2016, and La Niña events occur in 2005/2006, 2007/2008, and 2010/2011. These events are simulated well by the LICOM based on the Niño3 index from the OISST data (Fig.1). The correlation and root-mean-square error (RMSE) between the LICOM simulation and OISST are 0.87 and 0.4. Therefore, it is reasonable to use the LICOM simulation for analyses of ENSO events since this model can basically reproduce the individual ENSO events. Figure 2 shows interannual variability of SST anomalies simulated by the LICOM in comparison with the Hadley Center data averaged between 5°S and 5°N along the equator during 2000–2015. LICOM can reproduce the interannual variability of SST anomalies during ENSO events fairly well. Figure 3 shows the interannual variability of SLA from the LICOM simulation compared with AVISO altimeter data. The interannual anomalies from LICOM are based on monthly climatological averages from 2000 to 2015. Model can reproduce the interannual variability of SLA well in comparison with AVISO altimeter data except that slightly weaker SLA is simulated. In addition, LICOM reproduces fairly well the downwelling anomalies (positive SLA) in the eastern Pacifi c Ocean and upwelling anomalies (negative SLA) in the western Pacifi c Ocean during El Niño events. The correlation and RMSE between the simulated SLA and AVISO altimeter data in the Niño3 region are 0.88 and 3.6 cm, respectively. Therefore, the LICOM can be used to study the dynamics of the equatorial Pacifi c Ocean circulation during 2014–2016 El Niño events, which is also used for equatorial waves analysis in the study of Zhao et al. (2019).

Fig.3 Time-longitude plots of monthly SLA (unit: cm) averaged between 5°S–5°N along the equator during 2000-2015 from the AVISO altimeter data (a); the LICOM simulation (b); and time-longitude plot of monthly zonal wind stress anomalies (unit: Pa) (c)
Both model and observations show that the SLA and SST anomalies in the eastern Pacifi c Ocean in 2015 are much stronger than those in 2014 before mature phase of El Niño event, suggesting that a stronger El Niño event occurred in 2015. Stronger downwelling anomalies occurred in early 2014 (January–April) in comparison with SLA in early 2015 since upwelling anomalies dominated in the eastern equatorial Pacifi c Ocean in early 2015, which is consistent with the structure of zonal wind anomalies as shown in Fig.3c. The wind stress anomalies show that Westerly anomalies occurred in early 2014 and easterlies occurred in early 2015 in the western Pacifi c Ocean. However, stronger westerly anomalies did not result in a stronger El Niño event because the stronger WWBs activity lasted since March 2015, suggesting that the stronger El Niño event in 2015 may be related to the continuous WWBs in comparison with the wind stress anomalies in 2014.
3.2 Decomposed equatorial waves
Figure 4 shows the decomposed equatorial Kelvin wave and the fi rst meridional mode Rossby wave coefficients of the fi rst baroclinic mode during 2000–2015 using the wave decomposition method (Yuan et al., 2004). Here, we ignore the higher order baroclinic mode results since the second baroclinic mode contribution is energetic in the central and eastern equatorial Pacifi c Ocean in the mature warming of El Niño events (Dewitte et al., 1999, 2003). In addition, we are focusing the role of the western boundary reflection in the western Pacifi c Ocean. The decomposed wave coefficients are extracted from the LICOM output to study the wave dynamics of the SLA evolution during the 2014/2015 and 2015/2016 El Niño events. The evolution of the equatorial wave coefficients corresponds to that of SLA in Fig.3, suggesting the eastward propagation of downwelling equatorial Kelvin waves during El Niño events and of the upwelling equatorial Kelvin waves during La Niña events. The correlation between SLA and wave coefficients (Kelvin wave, Rossby wave) is over 0.8 in the western and eastern Pacifi c Ocean and slightly low in the central Pacifi c Ocean. Besides, the correlation between SLA and Rossby wave coefficients is higher than that between SLA and Kelvin wave coefficients. These suggest that the Kelvin wave from the reflection of Rossby wave at the western boundary may play an important role in the evolution of SLA.

Fig.4 Decomposed coefficients of the equatorial Kelvin wave (a) and the Rossby wave (b) of the fi rst baroclinic mode from the LICOM simulation
At the end of the El Niño years such as 2002, 2004, 2006, 2009, 2014, and 2015, upwelling equatorial Kelvin waves from the western boundary propagate eastward, following the propagation of downwelling equatorial Kelvin waves. The arrival of these upwelling equatorial Kelvin waves is coincident with the reversal of the SLA at the eastern boundary in the Pacifi c Ocean, suggesting that the downwelling anomalies in the eastern Pacifi c Ocean at the end of the El Niño years are terminated by these upwelling equatorial Kelvin waves from the western boundary. Upwelling equatorial Rossby waves consistently reach the western boundary at the end of El Niño years including 2002, 2004, 2006, 2009, 2014, and 2015. Based on the equatorial wave theory, upwelling equatorial Rossby waves can reflect into the upwelling equatorial Kelvin waves at the western boundary (Clarke, 1983), suggesting that the western boundary reflection may provide weakening impact during the evolution of the downwelling anomalies in the eastern Pacifi c Ocean and may inhibit the evolution of El Niño event. This phenomenon can be interpreted as the delayed oscillator theory during ENSO events (Schopf and Suarez, 1988). Figure 5 shows the time series of the equatorial wave coefficients at the western and eastern boundary from the LICOM simulation. The decomposed and reflected wave coefficients are plotted in red and green curves, respectively. Here, the reflected wave coefficients are calculated using the linear equatorial wave theory (Clarke, 1991) from the fi rst and the third meridional mode equatorial Rossby wave coefficients decomposed from the model output. The difference between the wave coefficients is plotted in blue curve. The fi rst meridional mode Rossby wave multiplied by its reflection coefficients (0.41) is plotted in orange curve. Here, the reflection coefficients are calculated using the linear theoretical value estimated for a straight coastline and low frequency waves (Clarke, 1983). The use of a 0.41 theoretical reflection coefficient appears to be an overestimation of how much energy can be expected to reflect off the western boundary as suggested by Spall and Pedlosky (2005). Therefore, the role of western boundary reflection may be overestimated. However, large differences can be noticed in Fig.5a; therefore, we ignored the discussion of the sensitivity of conclusions when using less efficient reflection coefficients. One reason for the differences may be the estimation of the reflected waves from the low-order baroclinic mode at the western boundary in the Pacifi c Ocean, while another may be from the strong nonlinearity that can be influenced by the complex structure of the nonlinear western boundary currents (Wang and Yuan, 2012, 2014). The reflection process of the Rossby waves at the western boundary is more complicated than the reflection of equatorial Kelvin wave at the eastern boundary because of the strong nonlinearity near the western boundary. Upwelling equatorial Kelvin waves, which propagate eastward and weaken the positive anomalies of SLA in the eastern Pacifi c Ocean, are detected in early 2014 and 2015 (Fig.5a, in red). At the eastern boundary, the Rossby waves are in good agreement with the linear reflection of the equatorial Kelvin waves (Fig.5b). Upwelling equatorial Rossby waves from the reflection of the Kelvin waves can be noticed in June–July 2014 (Fig.5b). However, only the downwelling equatorial Rossby waves can be observed after May 2015. The difference between 2014 and 2015 at the eastern and western boundaries may induce different downwelling anomalous evolution process during the 2014/2015 and 2015/2016 El Niño events.
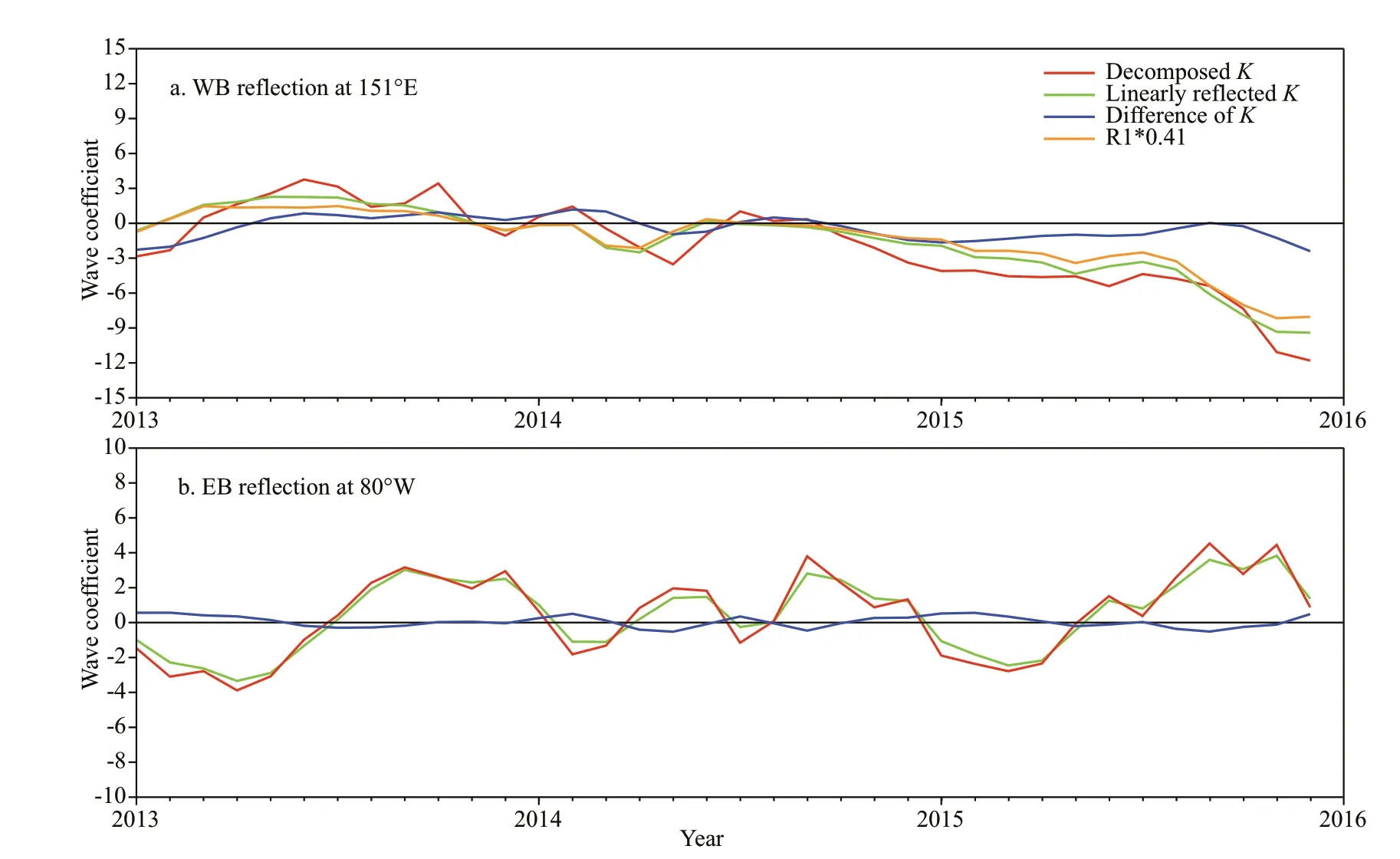
Fig.5 Decomposed wave coefficients at the western and eastern boundary
3.3 Interannual variations of SLA and equatorial wave dynamics during the 2014/2015 and 2015/2016 El Niño events
Figure 6 shows the time-longitude plots of decomposed Kelvin wave coefficients and the fi rst meridional mode Rossby wave coefficients of the fi rst baroclinic mode during 2013–2015. Downwelling Kelvin wave coefficients are seen to propagate eastward, with stronger coefficients seen in 2015 than those in 2014, suggesting that stronger westerly anomalies occur in 2015. This fi nding is consistent with the Hovmöller plot of zonal wind stress anomalies along the equator (Fig.3c). Upwelling equatorial Kelvin waves from the western boundary propagate to the eastern boundary in April 2014, terminating the dowelling Kelvin waves and inhibiting the downwelling anomalies in the eastern Pacifi c Ocean. However, no such equatorial Kelvin waves could propagate to the eastern boundary in the Pacifi c Ocean in summer 2015, suggesting that the upwelling equatorial Kelvin waves from western boundary reflection in early 2014 may have played an important role in weakening the downwelling anomalies in the eastern Pacifi c Ocean.

Fig.6 Time-longitude plots of decomposed wave coefficients, windstress anomalies and Niño 3 index
The evolution of downwelling anomalies instead of the sea surface temperature in the eastern Pacifi c Ocean is discussed for comparing the 2014/2015 with 2015/2016 El Niño events. For the 2015/2016 El Niño event, downwelling anomalies in the eastern Pacifi c Ocean occurred in boreal summer, developed in fall and peak in boreal winter. For 2014/2015 El Niño event, downwelling anomalies develop in early 2014 and decrease in July 2014. Although the downwelling anomalies peak in winter, SLA are largely weaker than those in 2015. To analyze the influence of equatorial waves on the evolution of SLA, SLA and wind stress anomalies in the tropical Pacifi c Ocean are compared from May to August in 2014 and 2015 (Fig.7).
Early 2014 experienced less WWBs activity than early 2015 from the view of longer period, which can also be seen in Fig.3c. In general, it will take two and a half months for the upwelling equatorial Kelvin waves to propagate to the eastern boundary of the Pacifi c Ocean based on the equatorial Kelvin wave speed of the fi rst baroclinic mode calculated by Chelton et al. (1998). Upwelling equatorial Kelvin waves generated at the western boundary in April 2014 reached the eastern boundary before July 2014 (Fig.6). SLA are reduced by at least 5 cm in July 2014 in the eastern Pacifi c Ocean in comparison with that in June 2014. It is evident that the decreasing of SLA magnitudes is closely related to the arrival of upwelling equatorial Kelvin waves. In contrast, SLA in July 2015 did not decrease in comparison with those in June since no weakening from upwelling equatorial Kelvin waves from the western Pacifi c Ocean in 2015 (Fig.6a). In addition, the evolution of SLA as indicated by the AVISO altimeter data is also consistent with the LICOM simulation (Fig.3a). A clear decrease in SLA occurred in July 2014. The Niño 3 index from the OISST data also shows a decrease in summer 2014, as shown in Fig.1, suggesting that the arrival of upwelling equatorial Kelvin wave indeed influenced the downwelling anomalies in the eastern Pacifi c Ocean. In addition, westerlies are stronger in May–August 2015 than those in 2014 in the western and central equatorial Pacifi c Ocean (Fig.7). WWBs-forced downwelling equatorial Kelvin waves propagate to the east and increase the downwelling anomalies (positive SLA) in the eastern Pacifi c Ocean in 2015. The SLA and westerly anomalies in August 2015 is evidently stronger than that in July 2015 (Fig.7, right panel). However, no evident increase of SLA in August 2014 compared with that in July 2014 is found in the eastern Pacifi c Ocean especially near the eastern boundary associated with weak WWBs. Therefore, there are two reasons of inducing a stronger El Niño event in 2015: one is the enhancing effects from the westerly anomalies forced downwelling equatorial Kelvin waves; and the other is the absence of weakening effects of upwelling equatorial Kelvin waves from the western boundary reflection in the western Pacifi c Ocean.

Fig.7 SLA (unit: cm) and wind stress anomalies (unit: Pa) from May to August in 2014 and 2015
3.4 Processes of western boundary reflection in the Pacifi c Ocean
To study the generation of the upwelling equatorial Kelvin waves from the western boundary, SLA along 5°N, the equator and zonal wind stress anomalies at the equator are shown in Fig.8. The upwelling Rossby waves at 5°N are well established at approximately 130°W in the eastern Pacifi c Ocean and are associated with the westerlies in Fig.8c, which propagate westward in the Pacifi c Ocean. In addition, the upwelling equatorial Kelvin waves are generated at the equator in phase with the arrival of the Rossby waves, which can be seen based on the structure of SLA at the equator (Fig.8b). This fi nding suggests that upwelling equatorial Kelvin waves are partially generated by the reflection of the upwelling equatorial Rossby waves. The large difference between the decomposed and linearly reflected equatorial Kelvin wave coefficients at the western boundary (Fig.5a) suggests that not all of the upwelling Kelvin waves are from the reflection of equatorial Rossby waves. A large negative SLA band is perceived in the latitudinal band of 20°S south of the equatorial Pacifi c Ocean (Fig.7, left panel). Therefore, the off-equatorial Rossby waves and strong nonlinearity also play a role in the generation of the upwelling Kelvin waves at the western boundary in early 2014. The nonlinear reflection process at the western Pacifi c Ocean is complicated, and is beyond the scope of the paper. We leave the details of nonlinear processes for future study.
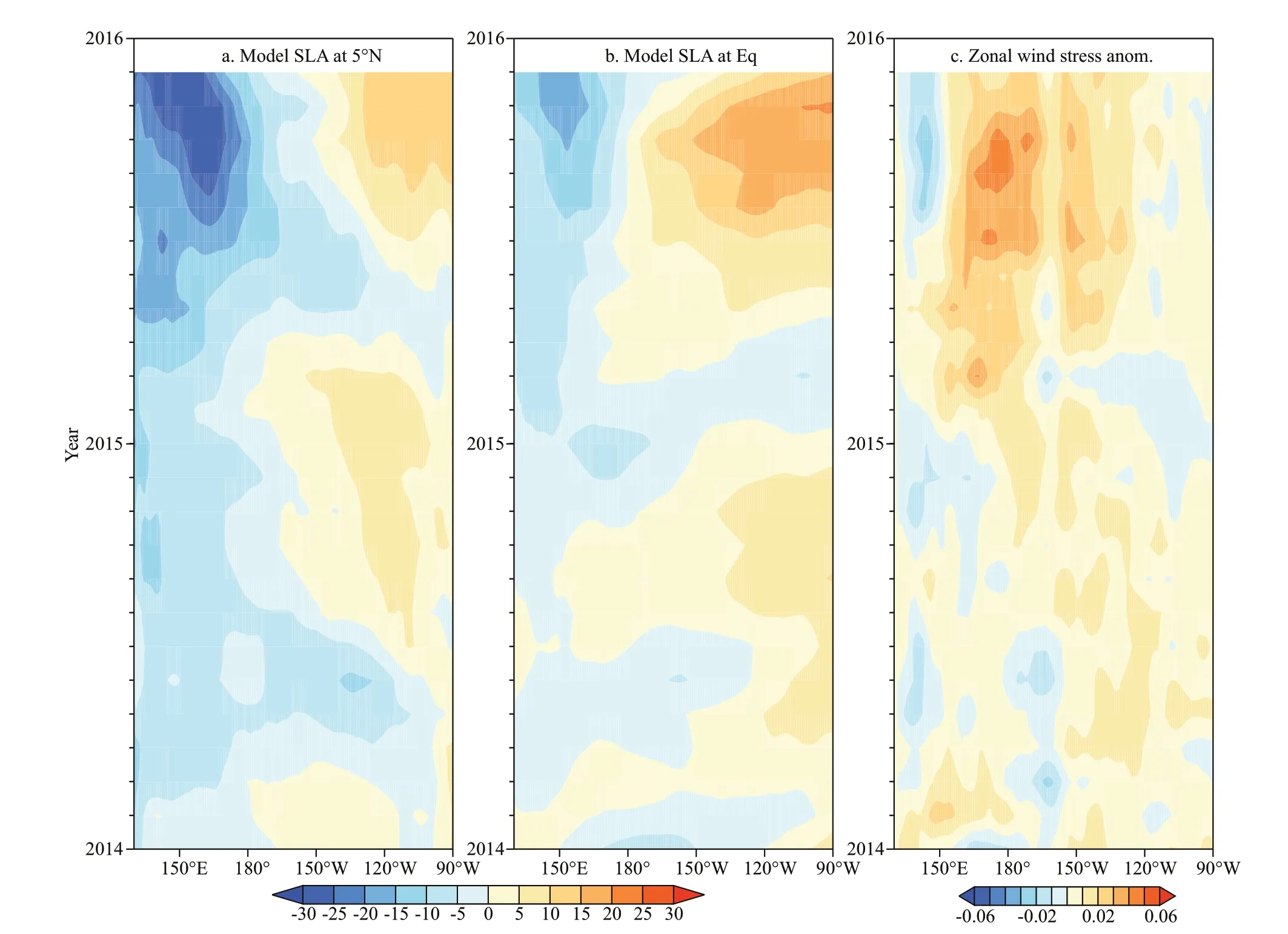
Fig.8 Time-longitude plots of SLA at 5°N (a), the equator (b), and the wind stress anomalies (c) during 2014–2015
Figure 8 shows a qualitative description of the generation of upwelling Kelvin waves at the western boundary. To study the equatorial upwelling Kelvin waves quantitatively, the wind-forced and westernboundary-forced equatorial Kelvin wave coefficients are compared using a linear wave model. The decomposed coefficients at 151°E are integrated along the characteristic lines for obtaining the net forcing from the western boundary without considering the influence of wind forcing in the Pacifi c Ocean. Figure 9 shows the time-longitude plots of the wind-forced equatorial Kelvin wave coefficients with zero conditions at the western boundary and western-boundary-forced equatorial Kelvin wave coefficients ignoring the influence of wind forcing and the sum of them. Stronger WWBsforced downwelling equatorial Kelvin waves can be observed in 2015 than in 2014, which is consistent with the amplitudes of WWBs (Fig.3c). In addition, the wind-forced upwelling equatorial Kelvin waves in 2014 and 2015 could not reach the eastern boundary in the Pacifi c Ocean. In contrast, western-boundaryforced upwelling equatorial Kelvin waves could arrive at the eastern boundary in 2014 and 2015 (Fig.9b). In addition, a stronger upwelling Kelvin wave could be seen in 2015 (Fig.6a), which was related to stronger WWBs-forced upwelling equatorial Rossby waves in the western Pacifi c Ocean (Fig.6b). However, the upwelling equatorial Kelvin waves from western boundary could not reach the eastern boundary in 2015 (Fig.6a), a phenomenon which was associated with the overwhelming WWBs-forced downwelling equatorial Kelvin waves seen in 2014. The sum of western-boundary-forced and windforced equatorial Kelvin wave (Fig.9c) is largely consistent with the decomposed equatorial wave (Fig.6a), suggesting that linear wave theory is applicable to reproduce the decomposed wave coefficients. The propagation of upwelling equatorial Kelvin waves from the western boundary weakened the downwelling anomalies (positive SLA) in the eastern Pacifi c Ocean in 2014. Weak WWBs limit the generation of downwelling equatorial Kelvin waves, suggesting no enhancing effects are provided. Therefore, no strong El Niño event can occur in 2014 in comparison with the 2015/2016 El Niño event. In contrast, continuous WWBs-forced downwelling Kelvin waves constantly generated in 2015 accelerated the downwelling anomalies in the eastern Pacifi c Ocean, which yielded a strong El Niño event (Levine and McPhaden, 2016).
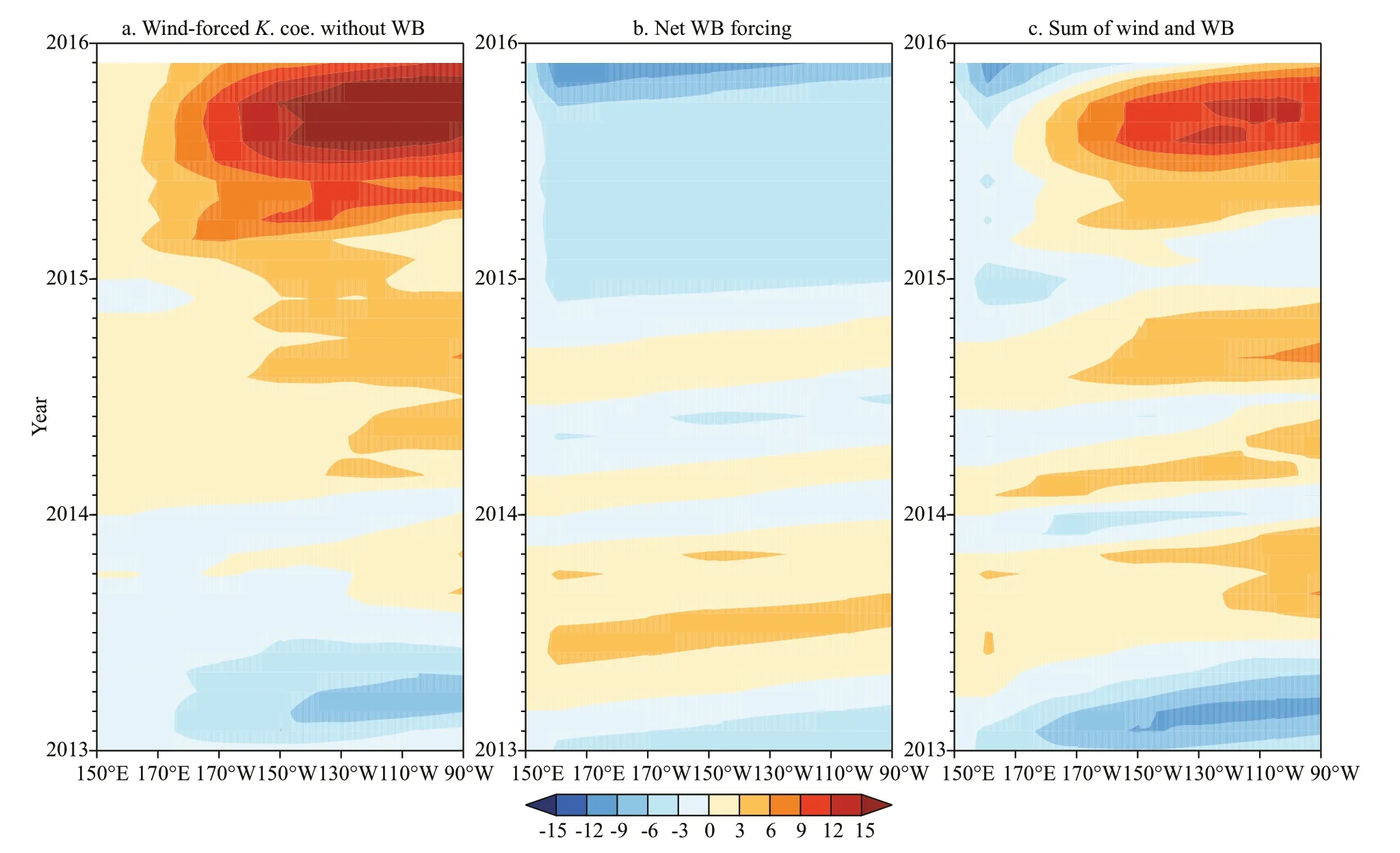
Fig.9 Time-longitude plots of wind-forced equatorial Kevin wave coefficients setting western boundary wave condition (151°E) to zero values (a); western-boundary-forced equatorial Kelvin wave coefficients (b)
4 DISCUSSION
A strong El Niño event occurred in 1997. The spring conditions of the zonal wind anomalies in 1997 are similar to those in 2014. However, the strong WWBs occur in the western and central equatorial Pacifi c Ocean in May 1997 while no such winds occurred in 2014 (Yuan et al., 2004; Chen et al., 2015). Figure 10 shows the time-longitude plots of decomposed Kelvin wave coefficients (a) and the fi rst meridional mode Rossby wave coefficients (b) of the fi rst baroclinic mode from LICOM simulation during 1997–1999. Stronger downwelling equatorial Kelvin waves associated with WWBs propagate eastward during the 1997/1998 El Niño event. This fi nding is consistent with the zonal wind anomalies in 1997 (Fig.10c). Upwelling equatorial Kelvin waves from the western boundary could not reach the eastern Pacifi c Ocean, which is similar to 2015/2016 El Niño event. WWBs-forced equatorial Kelvin wave coefficients are also calculated as shown in Fig.11. Upwelling equatorial Kelvin waves from WWBs forcing could not arrive at the eastern boundary in 1997. However, upwelling equatorial Kelvin waves from the western boundary could indeed reach the eastern boundary. This fi nding suggests that the contribution of the strong WWBs-forced downwelling equatorial Kelvin waves overwhelm that of the upwelling equatorial Kelvin waves from the western boundary. The western boundary reflection process in 1997/1998 El Niño is similar to 2015/2016 El Niño. In contrast, western boundary reflections in summer 2014 play an important role in inhibiting the developing of the 2014/2015 El Niño event. An artifi cial western boundary is set at 151°E in this paper due to consideration that the process of western boundary reflection is complex in the perforated western boundary in the Pacifi c Ocean. However, nonlinear processes of the western boundary reflection occur and the linear theory cannot be applied to the west of 151°E in the western Pacifi c Ocean. Therefore, the role of the easterly wind anomalies in the west of 151°E is easily mistaken as the western boundary when calculating the western-boundary-forced Kelvin wave coefficients. Figure 8c shows the time-longitude plot of zonal wind stress anomalies during 2014–2015. Weak easterly wind anomalies appeared from March 2014 and began to increase in May 2014 to the west of 150°E. In the meantime, easterly wind anomalies also occur near 165°W and were stronger than those anomalies to the west of 150°E. Therefore, stronger upwelling Kelvin waves are purportedly generated near 165°W than west of 151°E in a linear model. Wind-forced upwelling Kelvin waves near 165°W, which can be seen in Fig.9a using a linear wave model, could only propagate to 140°W and cannot reach the eastern boundary in 2014. Therefore, upwelling equatorial Kelvin waves forced by the easterly wind anomalies to the west of 150°E could not reach the eastern boundary in both a linear and qualitative view. Energies are assumed to dissipate more during the eastward propagation of upwelling equatorial Kelvin waves far to west of 150°E than those near 165°W. From the view of linear equatorial wave dynamics, our study gives a possible explanation the inhibited growth of the 2014/2015 El Niño events, which differs from explanations provided by previous studies (Menkes et al., 2014; Hu and Fedorov, 2016).

Fig.10 Time-longitude plots of decomposed Kelvin wave coefficients (a) and the fi rst meridional mode Rossby wave coefficients (b) of the fi rst baroclinic mode from LICOM simulation during 1997–1998; zonal wind stress anomalies during 1996–1998 (c); Niño 3 index during 1996–1998 (d)

Fig.11 Time-longitude plots of wind-forced equatorial Kevin wave coefficients setting western boundary wave condition (151°E) to zero values (a); western-boundary-forced equatorial Kelvin wave coefficients during 1996–1998 (b); sum of the wind-forced and western-boundary-forced equatorial Kelvin wave coefficients (c)
5 CONCLUSION
Long equatorial wave dynamics of interannual sea level variations during 2014/2015 and 2015/2016 El Niño events are compared using a LICOM simulation forced by wind stress and heat flux data from the daily NCEP reanalysis I data during 1948–2015. The LICOM can reproduce the SST anomalies and SLA along the equator over the equatorial Pacifi c Ocean in comparison with TAO data and AVISO altimeter SLA data well, and can simulate the interannual variability of the SSTA and SLA well including individual El Niño and La Niña events. The equatorial wave coefficients are extracted from LICOM simulation to study the role of the propagation and reflection of the equatorial waves in the evolution of SLA during El Niño events. Signifi cant differences in equatorial waves are analyzed. The responses of the Pacifi c Ocean to winds are further explored.
Upwelling equatorial Kelvin waves from the western boundary in April 2014 propagated to the eastern Pacifi c Ocean, which terminated the downwelling equatorial Kelvin waves in the east and weakened the downwelling anomalies (positive SLA) in the eastern Pacifi c Ocean. However, no such upwelling equatorial Kelvin waves from the western boundary in the Pacifi c Ocean can reach the eastern boundary during 1997/1998 and 2015/2016 El Niño events. The role of zonal wind forcing and western boundary reflection are compared during 2014/2015 and 2015/2016 El Niño events by calculating the equatorial Kelvin wave coefficients using a linear characteristic wave model. The results demonstrate that the upwelling equatorial Kelvin waves in 2014 are originated partially from the reflection of equatorial Rossby wave at the western boundary in the Pacifi c Ocean. In addition, off-equatorial Rossby wave and nonlinearity also play a role. Here, we only provide a qualitative explanation. Although upwelling Kelvin wave associated with western boundary reflection in 2015 was stronger than that in 2014, stronger westerly anomalies-forced downwelling equatorial Kelvin waves overwhelmed the role of the western boundary reflection in 2015 since stronger continuous westerly anomalies occurred in 2015 and only weak westerly anomalies occurred after April 2014. Therefore, both the western boundary reflection and weak WWBs inhibit the growth of the 2014/2015 El Niño event.
The analyses presented in this paper suggest that the propagation and reflection of equatorial waves in the Pacifi c Ocean play an important role in the interannual variability of the downwelling anomalies in the eastern Pacifi c Ocean during El Niño events. Western boundary reflections provide a weakening effect to the growth of El Niño event. The comparison between linear reflection and decomposed wave coefficients suggests that upwelling equatorial Kelvin waves generated in April 2014 were not only due to the reflection of equatorial Rossby waves but also due to off-equatorial Rossby waves and nonlinearities. This paper provides a possible mechanism for the inhibition of the growth of an El Niño event, and further studies are needed to study the prediction of interannual variability of the tropical climate in the Pacifi c Ocean and how WWBs activities affect the maintenance or growth of induced warming anomaly or positive SLA. These studies may have useful forecasting implications. In addition, the processes of western boundary reflection to the west of 151°E in the Pacifi c Ocean need to be analyzed using the model simulation and observational data since we ignore the complicated western boundary reflection process in this paper for simplicity. The disclosed equatorial wave dynamics are important for the evolution and predictability of ENSO events.
6 DATA AVAILABILITY STATEMENT
All data generated and/or analyzed during this study are available from the corresponding author on request.
7 ACKNOWLEDGMENT
We are grateful to the two anonymous reviewers for their insightful comments and suggestions.
 Journal of Oceanology and Limnology2020年4期
Journal of Oceanology and Limnology2020年4期
- Journal of Oceanology and Limnology的其它文章
- Review on observational studies of western tropical Pacifi c Ocean circulation and climate*
- Research progress of TiO 2 photocathodic protection to metals in marine environment*
- Smart anticorrosion coating based on stimuli-responsive micro/nanocontainer: a review*
- Status of genetic studies and breeding of Saccharina japonica in China*
- To be the best in marine sciences*
- A review of progress in coupled ocean-atmosphere model developments for ENSO studies in China*
