考虑环境外部成本的多式联运路径优化研究

贾叶子 李博威

(西南交通大学交通运输与物流学院1) 成都 611756) (广西交通设计集团有限公司2) 南宁 530029)

0 引 言

多式联运作为一种创新的运输组织形式，已经成为现代物流运输的主要方式.但交通运输业的快速发展在促进经济增长的同时也带来了很多外部效应，如空气污染、气候变化、噪声污染等.将环境外部成本纳入多式联运路径优化的成本计算中，对于促进多式联运的绿色低碳发展具有重要的现实意义.

国内外学者在多式联运路径优化方面已做了很多工作.Chang[1]对多式联运路径选择问题建立了多目标模型，同时考虑在时间窗约束下的多种商品流的路径分配；Hanafi等[2]将欧洲碳排放政策作为影响多式联运路径选择的重要因素，将减少碳排放成本(主要表现为碳税)作为模型目标之一；Xiong等[3]针对多式联运路径规划“费用一时间”双目标优化问题进行了建模研究，费用最低和时间最省被同时设定为模型的优化目标；刘杰等[4]提出节点运输方式备选集，建立基于运输方式备选集的多式联运动态路径优化模型；王清斌等[5]研究集装箱多式联运在运输方式转换过程中节点作业随机特征对运输方式和路径选择的影响,以总成本最小为目标，建立带有时间约束的混合整数规划模型；蒋洋等[6]提出了针对多式联运运输方案选择问题的交叉熵算法，并给出了计算步骤和相应的计算方法；王慧等[7]考虑运输需求量为模糊情况下，建立集装箱多式联运箱型和运输方式的优化模型，实现集装箱多式联运总成本最优化，并提出模型求解的改进型粒子蚁群算法；于雪峤等[8]利用精确求解方法验证了带时间窗与客户满意度约束的单商品流单目标多式联运路径选择模型的有效性.

综上，现有的关于多式联运路径优化方面的研究多以运输时间、运输成本或运输服务水平中的一个或多个为目标建立模型，而较少从环保角度出发研究多式联运路径选择，且现有的研究一般以碳排放成本作为目标，而忽略了空气污染、噪声污染等外部效应产生的环境外部成本.本文在已有研究的基础上，建立考虑环境外部成本的多式联运路径优化模型，为决策者进行路径选择时提供理论依据.

1 多式联运环境外部成本计算

1.1 空气污染成本计算

借鉴文献[9]中的排放成本模型，计算式为

(1)

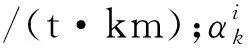
1.2 气候变化成本计算

本文在计算气候变化成本时以CO2排放成本衡量价值损失.目前CO2排放成本的计算方法主要有避免成本法和损害成本法，由于当前研究者对气候变化带来的影响仍没有较一致的共识，因此采用这两种方法评估的CO2排放成本具有较大的不确定性.本文参考文献[10]中CO2排放量的计算公式计算不同运输方式的单位CO2排放量，结合碳排放税可求得不同运输方式的单位气候变化成本，计算公式为

eck=10-6·taxc·wk

(2)

式中：eck为第k种运输方式的单位气候变化成本，元/(t·km)；taxc为碳排放税(CO2的影子价格)，元/t；wk为第k种运输方式的单位CO2排放量，g/(t·km).

文献[12]中CO2排放量的计算公式如下，其中公路运输和水路运输主要通过燃油消耗产生CO2，铁路运输目前主要采用电力机车牵引，虽然在运输过程中不产生CO2，但应考虑为其供电的发电企业产生的CO2排放.

wk=gk·fk

(3)

式中：wk为第k种运输方式的单位CO2排放量，g/(t·km)；gk为第k种运输方式的单位能源消耗量，L/(t·km)或kW·h/(t·km)；fk为第k种运输方式的排放系数，即单位能源消耗所排放的CO2量，kg/L或kg/(kW·h).

1.3 噪声污染成本计算

本文参照欧洲在噪声成本研究中的成果，对我国不同运输方式的噪声成本进行类推比较.根据文献[10]，通过调整人口密度指标和人均GDP指标获得我国的噪声污染成本，计算公式为

enk=r·enuk·βg·βp

(4)

式中：enk为我国第k种运输方式的单位噪声污染成本，元/(t·km)；enuk为欧洲第k种运输方式的单位噪声污染成本，欧元/(t·km)；r为欧元对人民币的平均汇率；βg为人均GDP调整系数(我国与欧洲的人均GDP比值)；βp为人口密度调整系数(我国与欧洲的人口密度比值).

2 问题描述及模型建立

2.1 问题描述

某货主有一批货物需要从起始地O运送到目的地D，货物从起始地到目的地会经过若干个转运节点，每两个相互连通的节点之间可通过铁路、公路、水路三种运输方式进行运输，每种运输方式的运输成本和运输时间不同.每个转运节点处可选择一种运输方式转换，由此产生相应的转运时间和转运成本.在考虑多式联运环境外部成本的条件下，确定该批货物最优的运输方案.

2.2 模型假设及符号说明

为便于建模，作出假设如下：①多式联运过程中集装箱货物不拼箱、不拆箱；②任意两个相邻节点之间最多只能选择一种运输方式；③只能在转运节点进行转运，每个节点最多有一次运输方式的转换；④节点处的设备条件能满足运输方式之间转换的要求；⑤不考虑转运过程中的环境外部成本；⑥不考虑载运工具和装卸设备故障等因素对运输费用和运输时间的影响.

本文所建模型的相关参数及变量说明见表1～2.

表1 参数说明

表2 决策变量说明

2.3 模型建立

基于上述假设，本文建立的考虑环境外部成本的多式联运路径优化模型如下.

(5)

(6)

(7)

(8)

(9)

(10)

(11)

(12)

(13)

式(5)为运输总成本目标函数，表示多式联运运输总成本最小，运输总成本包括节点之间的运输成本、集装箱租赁成本和节点的转运成本；式(6)为环境外部成本目标函数，表示多式联运环境外部成本最小，环境外部成本包括空气污染成本、气候变化成本和噪声污染成本；式(7)为运输总时间目标函数，表示多式联运运输总时间最小，运输总时间包括节点之间的运输总时间和节点的转运总时间；式(8)～(13)为约束条件，式(8)为货流平衡约束，表示进入节点i的货流量与转出节点i的货流量相等，从而保证货物运输过程中的不可拆分性；式(9)为任意两个相邻节点i与j之间最多只能选择一种运输方式；式(10)为集装箱在转运节点i处最多有一次运输方式的转换；式(11)为连续性约束，表示集装箱在节点j选择由第k种运输方式转换为第l种运输方式时，则集装箱从节点i运输到节点j时必须采用第k种运输方式，从节点j运输到节点h时必须采用第l种运输方式；式(12)和式(13)为决策变量约束.

2.4 模型求解

上述模型为多目标规划问题，为便于求解，需将多目标规划问题转化为单目标规划问题.本文借助模糊优化中的理想点法，将求解多目标规划问题转化为求解以加权欧式距离为目标的单目标规划问题.具体求解步骤如下.

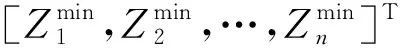
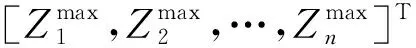
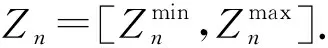
步骤4归一化处理.由于各目标值的量纲不同，为了统一量纲，需对各目标值进行归一化处理，归一化公式为式(14)和(15).

(14)

(15)

步骤5建立如式(16)的单目标规划问题，使多目标规划问题中某一可行解的目标值与正理想点的加权欧式距离达到最小.

(16)

式中：wn为第n个目标的权重，体现目标的重要程度.

通过上述步骤，多目标规划问题转化为以加权欧氏距离最小为目标的单目标规划问题，借助优化求解器LINGO可进行求解.

3 算例分析

3.1 算例数据

假定有一批货物采用TEU集装箱从起始地O(节点1)运送至目的地D(节点35)，货物共有10 TEU，每TEU货物的重量为10 t，起始地与目的地之间有33个节点城市，每两个节点之间最多有三种运输方式可供选择，分别为公路、铁路、水路，多式联运网络图见图1.每标箱日租赁成本为100元/d，欧元对人民币平均汇率为7.852 3(2018年)，人均GDP调整系数为0.26，人口密度调整系数为1.19，碳排放税为40元/t.在目标函数权重取值上，本文从多式联运承运人角度出发，更多考虑运输成本和运输时间对运输路径的影响，而环境外部成本所占比重较小，据此设定权重取值为w1=0.5，w2=0.2，w3=0.3，同时后文对权重变化产生的影响作进一步分析.各节点之间的运输距离参考文献[10]，限于篇幅未列出，三种运输方式的概况见表3，三种运输方式的污染物单位排放量见表4，空气污染物排放单价见表5，2010年欧洲噪声污染情况见表6，三种运输方式之间的转运情况见表7.

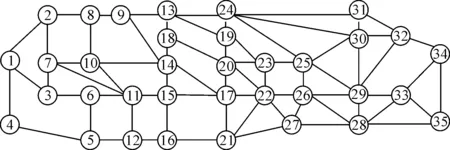
图1 多式联运网络图

表3 三种运输方式的概况

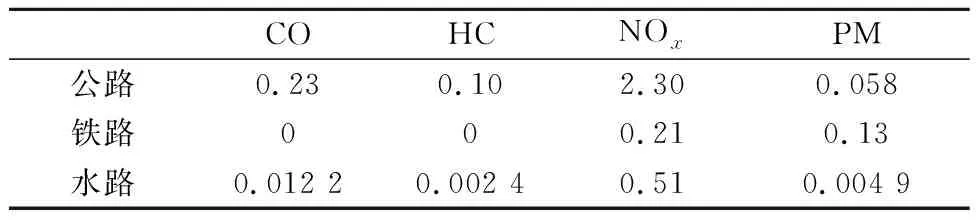
表4 三种运输方式的污染物单位排放量g/(t·km)

表5 空气污染物排放单价 元/kg

表6 2010年欧洲的噪声总成本和平均单位噪声成本预测值

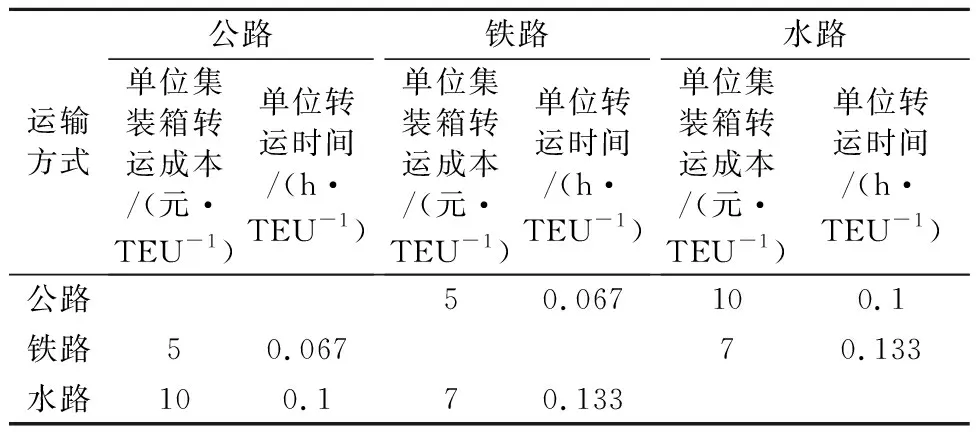
表7 三种运输方式之间的转运情况

在CO2排放量的计算上，公路运输中，我国目前使用的集装箱卡车大多为柴油机型，在载重10 t情况下，油耗取17 L/100 km，根据BP中国碳排放计算器提供的资料，柴油排放系数取2.63 kg/L；铁路运输中，铁路电力机车在运输过程中应考虑发电企业的CO2排放，根据国家统计局统计的国家铁路运输主要技术经济指标，2010年电力机车耗电为100.6 kW·h/(万t·km)，电力排放系数取0.717 kg/(kW·h)；水路运输中，集装箱船以柴油发动机为主，以装载量7 800 t集装箱船为例，航速16.80 kn,额定功率7 500 kW，燃油消耗率195 g/(kW·h)，消耗燃油1 462.5 kg，柴油排放系数取3.06 kg/kg.由式(3)分别计算得公路运输单位CO2排放量为44.71 g/(t·km)，铁路运输单位CO2排放量为7.21 g/(t·km)，水路运输单位CO2排放量为18.44 g/(t·km).

3.2 算例求解

基于多式联运网络和算例数据，运用LINGO12.0中的分支定界法分别对以运输总成本、环境外部成本和运输时间为目标的单目标规划问题进行求解，得到各目标的最优解和最劣解，见表8.

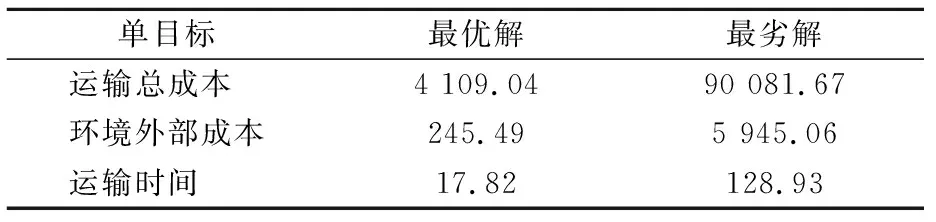
表8 各单目标对应最优及最劣目标值

由式(14)和式(15)对目标值及正理想点进行归一化处理后，根据式(16)建立以加权欧氏距离为目标的单目标规划模型，目标函数为

(17)

运用LINGO12.0对上述单目标规划模型进行求解，同时，为验证本文模型的有效性，将以运输总成本和运输时间为目标函数的多目标规划模型通过理想点法转化为单目标规划模型进行求解后，再与本文所建模型的求解结果进行对比，见表9，运输路线见图2.

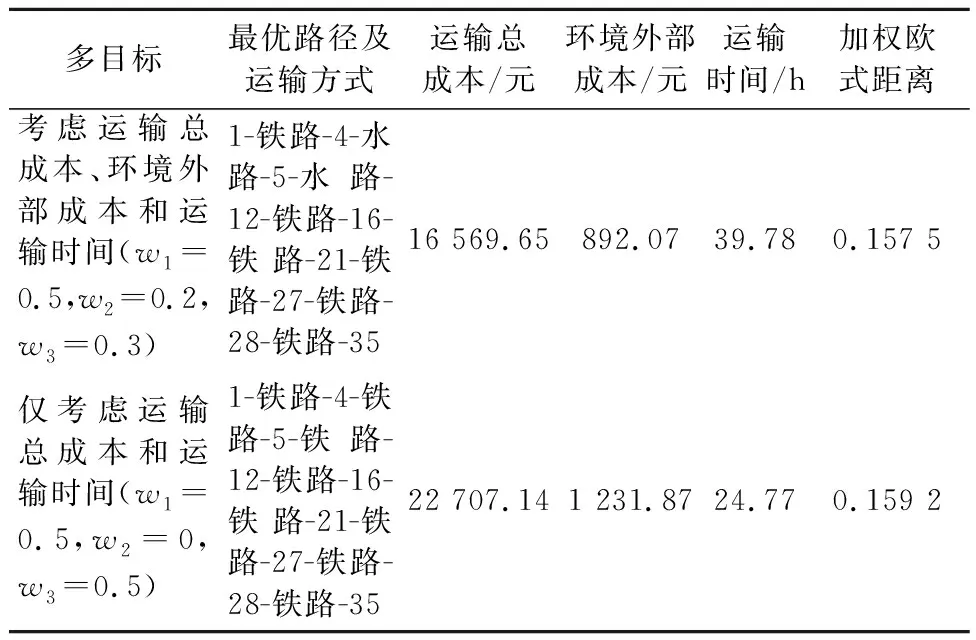
表9 对比结果

图2 运输路线图

由表9可知，与考虑环境外部成本相比，在未考虑环境外部成本时，虽然运输时间有所下降，但运输总成本和环境外部成本均显著增加，考虑环境外部成本所得到的结果不劣于仅考虑运输总成本和运输时间所得到的结果，因此，本文所建的模型较好地平衡了运输总成本、运输时间，以及环境外部成本之间的关系，考虑环境外部成本符合我国环境保护和节能减排的发展要求，可为多式联运决策者提供符合需求的运输方案.

为探究权重取值对求解结果的影响，在其他变量参数不变的情况下，改变运输总成本、环境外部成本和运输时间的权重取值，权重以0.1的梯度赋值，并将各权重组合下多式联运与单一运输方式的多目标理想点最优解进行对比，求解结果经MATLAB二元插值拟合后，见图3.

图3 各权重组合下多式联运与单一运输方式多目标理想点最优解对比

由图3可知：

1) 不同权重组合下公路、铁路和水路在多目标理想点最优解下的环境外部成本均未发生变化，公路环境外部成本最高，为2 377.49元，水路环境外部成本最低，为245.49元，铁路环境外部成本介于公路和水路之间，为1 231.868元，多式联运的环境外部成本随权重组合变化而发生变化，当运输总成本权重介于0～0.4，环境外部成本介于0～0.3时，多式联运环境外部成本介于公路和铁路环境外部成本之间，当运输总成本权重介于0.5～1，环境外部成本权重介于0.4～1时，多式联运环境外部成本介于铁路和水路环境外部成本之间，可见随着环境外部成本权重的不断增加，多式联运环境外部成本不断降低.

2) 不同权重组合下公路、铁路和水路在多目标理想点最优解下的运输总成本均未发生变化，公路运输总成本最高，为36 382.5元，水路运输总成本最低，为4 109.04元，铁路运输总成本介于公路和水路之间，为22 707.14元，多式联运的运输总成本随权重组合变化而发生变化，当运输总成本权重介于0～0.4，环境外部成本权重介于0～0.4时，多式联运运输总成本介于公路和铁路运输总成本之间，当运输总成本和环境外部成本权重介于0.5～1时，多式联运运输成本介于铁路和水路运输成本之间，可见随着运输总成本权重的不断增加，多式联运运输总成本不断下降，且不同权重组合下多式联运运输总成本和环境外部成本最优解变化趋势相似.

3) 不同权重组合下公路、铁路和水路在多目标理想点最优解下的运输时间均未发生变化，水路运输时间最长，为68.87 h，公路运输时间最短，为17.82 h，铁路运输时间介于水路和公路之间，为24.77 h，多式联运运输时间随权重组合变化而发生变化，当运输总成本权重介于0.5～1，环境外部成本权重介于0.4～1时，多式联运运输时间介于水路和铁路运输时间之间，当运输总成本权重介于0～0.4，环境外部成本权重介于0～0.3时，多式联运运输时间介于铁路和公路运输时间之间，可见随着运输时间权重的不断增加，多式联运运输时间不断下降.

当前我国对如何减少空气污染和噪声污染产生的环境外部成本还未作出明确规定，而在气候变化成本的控制上，虽然我国尚未开展征收碳排放税，但财政部和环保部对碳排放税的征收已进行了一些研究.随着我国对环境保护和节能减排的日益重视，未来碳税价格可能会逐步提高，相应的环境外部成本也会不断增加，多式联运决策者在制定运输方案时也必然会将环境外部成本作为一个重要因素予以考虑，因此加快制定碳税标准并出台相关政策是我国推进节能减排的重要途径之一.

4 结 束 语

本文考虑了空气污染、气候变化和噪声污染产生的环境外部成本对多式联运运输方式和路径选择的影响，详细阐述了各种运输方式的环境外部成本计算方法，以运输总成本、环境外部成本和运输时间作为优化目标建立了多式联运路径优化的多目标规划模型，在模型求解上，通过借助模糊优化中的理想点法将多目标规划模型转化为以加权欧式距离最小为目标的单目标规划模型，设计算例并利用LINGO12.0进行求解，算例求解结果表明本文所建模型能够较好平衡运输总成本、环境外部成本和运输时间三个相互冲突的目标，实现多式联运运输决策中多目标的协调，同时本文将环境外部成本纳入多式联运总成本中，符合我国推进节能减排的社会要求，可为多式联运路径选择和运输方案制定提供参考.为简化模型，本文未考虑不同货物品类在运输成本、运输时间和环境外部成本上的取舍差异，这也是后续将进行的工作.