基于不同网形的短边GPS控制网精度分析
申洋洋


摘 要:GPS可实现高精度定位,已广泛应用于各种大型工程,但短边GPS控制网在小型工程中的应用少有人关注。本文以郑州市某高校为测区,以三等导线网为基准对比分析四种不同网形精度,结果表明:c网形精度最高,达到《工程测量规范》(GB 50026—2007)三等精度;第三种方案精度最高;四种网形均适用于地形测量、地籍测量、土地测量、建筑施工测量、水利施工测量、土地整理及土地确权。
关键词:GPS控制网;数据处理;精度分析
中图分类号:P228.4文献标识码:A文章编号:1003-5168(2020)16-0008-05
Abstract: GPS can achieve high-precision positioning, has been widely used in various large-scale projects, but the application of short-side GPS control network in small-scale projects has received little attention. In this paper, a university in Zhengzhou was taken as a survey area, and the three-class traverse network was taken as a benchmark to compare and analyze the accuracy of four different network forms. The results show that the C network form has the highest accuracy, reaching the third-class accuracy in the code for Engineering Survey (GB 50026—2007) , and the third scheme has the highest accuracy. The four types of network are suitable for topographic survey, cadastral survey, land survey, construction survey, water conservancy survey, land arrangement and land right determination.
Keywords: GPS Control Network;data processing;precision analysis
GPS(Global Positioning System)即全球定位系统,是由美国国防部研制建立的一种全天候、全方位、全时段、高精度的卫星导航系统[1],能实时为全球用户提供精确的三维位置、速度和导航信息。GPS操作简便、精度高且相邻两点之间无须通视,已被广泛应用于测量工作中[2]。GPS技术的不断发展提高了测量工作效率,并且提供了更精密的数据,是目前最重要的对地观测技术[3]。国内外学者应用不同的GPS控制网进行了较多研究。例如,修涛[4]、王天仓[5]等总结了GPS控制网在可靠性、经济性等方面的特点,并提出了GPS控制网优化设计的措施;刘钰[6]、王于[7]、穆宁[8]等就GPS控制測量平面与高程精度展开了具体研究。目前对长边GPS控制网研究较多,如唐凯[9]结合县级尺度GPS控制测量实践,完成了具体的平面及高程数据处理;郝伟涛[10]以省级尺度D、E级GPS加密控制测量为例,设计加密控制网的布设、观测及数据处理方案。本文以郑州市某高校为测区,通过实例对不同网形、不同方案的短边GPS控制网精度进行分析与研究。
1 材料与方法
1.1 测区概况
本试验研究区域为河南省郑州市某高校,地处北纬34°47′~34°48′,东经113°47′~113°49′,位于华北平原南部,地势平坦,北临黄河,西依嵩山,学校占地面积1.267 km2。测区位于学校外围的主要干道,全长4.2 km,树木较多,西侧有高压线。
1.2 优化设计指标及布网方案
1.2.1 优化设计指标。GPS网形设计是GPS测量的第一步,是制订观测方案的重要过程,其设计指标可以归纳为以下几类。
1.2.2 布网方案。依据网形优化设计指标,结合工程测图、放样及监测的要求,在测区布设11个控制点,选择不同数量、不同位置的控制点布设4种不同的网形。第一种网形共布设9个控制点。研究受高压线影响但不受树木的影响下,3台接收机观测的GPS精度。第二种网形共布设9个控制点,研究在与第一种网形条件相同的情况下,用4台接收机观测的GPS精度。第三种网形共布设5个控制点。研究在不受树木、高压线的影响下,对网形简化、加大边长时使用3台接收机观测的GPS精度。第四种网形共布设11个控制点,研究同时受高压线、树木的影响下,使用3台接收机观测的GPS的精度。4种网形每时段的观测时间均为60 min。
1.3 试验执行的标准及主要技术指标
1.3.1 技术标准。测量依据《工程测量规范》(GB 50026—2007)和《全球定位系统(GPS)测量规范》(GB/T 18314—2001)。
1.3.2 主要技术指标。卫星定位测量控制网的主要技术指标如表1所示。
1.4 主要技术方法
本试验使用HGO数据处理软件对采集的数据进行基线解算和网平差处理。通过不同网形和同一网形内不同方案的对比,分析已知数据的数量和分布位置对网形精度的影响,确定布设精度最高的网形和方案。
2 GPS测量数据处理
GPS的数据处理是对观测值进行基线向量解算和网平差。
2.1 基线向量解算
基线向量解算质量控制指标为参考指标和控制指标。参考指标主要包括RMS值、RATIO值、RDOP值;控制指标包括数据删除率、复测基线长度较差、同步环闭合差、异步环闭合差。
经检验,本试验布设的4种网形,参与平差计算的基线,其重复基线较差、同步环闭合差、异步环闭合差均符合规范要求。
2.2 GPS网的平差
2.2.1 网平差指标。无约束平差中,基线分量的改正数绝对值[VΔX、VΔY、VΔZ]应满足:[VΔX≤3σ]、[VΔY≤3σ]、[VΔZ≤3σ],其中[σ]为相应等级规定的基线精度。
约束平差中,基线分量的改正数与合格三维无约束平差的同一基线向量改正数的绝对值应满足[dVΔX≤2σ]、[dVΔY≤2σ]、[dVΔZ≤2σ]。
2.2.2 无约束平差。无约束平差是不引入外部起算数据的网平差。一般GPS网平差采用间接平差法[13],其模型有两种,即函数模型和随机模型。
使用南方平差易对数据平差得控制网平差报告。由报告知,导线点中最大点位误差[G06]=0.021 9 m,最小点位误差[G02]=0.009 2 m,平均点位误差=0.015 6 m,最大点间误差=0.015 5 m,往返测距单位权中误差=0.000 m。由闭合差统计表可知,角度闭合差为3.1 s,全长相对闭合差[k]=1/72 613,符合《工程测量规范》(GB 50026—2007)精度要求。
3.2 网形指标分析
3.2.1 统计分析。对不同网形、不同方案的最弱点点位中误差进行统计、对比分析。
3.2.1.1 网形之间的对比分析。第一种方案和第二种方案(2个已知数据)中,最弱点点位中误差和最弱边相对中误差最小的为c网形;第三种方案和第四种方案(3个已知数据)中,最弱点点位中误差和最弱边相对中误差最小的为b网形。这4种方案中最弱点点位中误差和最弱边相对中误差最大的均为d网形。
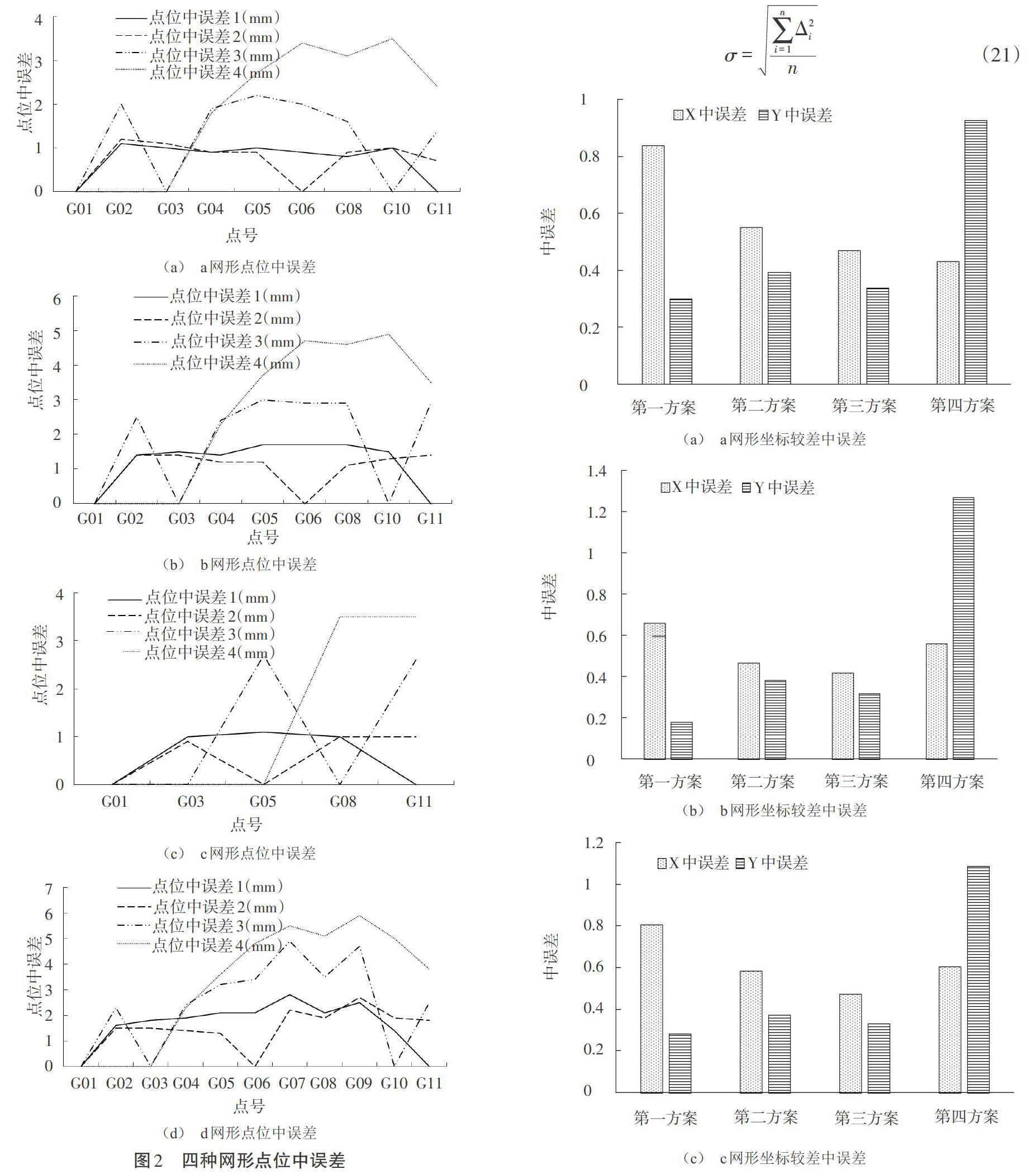
3.2.1.2 网形内不同方案的对比分析。a网形中第二种方案最弱点点位中误差最小(1.45 mm),第四种方案最弱点点位中误差最大(4.86 mm);b网形中第一种方案最弱点点位中误差最小(1.11 mm),第四种方案最弱点点位中误差最大(3.47 mm);c网形中第二种方案最弱点点位中误差最小(1.01 mm),第四种方案最弱点点位中误差最大(3.51 mm);d网形中第二种方案最弱点点位中误差最小(2.71 mm),第四种方案最弱点点位中误差最大(5.95 mm)。
3.2.2 点位中误差比较分析。每种网形使用4种方案进行平差,平差后的点位中误差如图2所示。比较不同方案的点位中误差,分析各种网形、各种方案的精度。
由統计分析可知,d网形精度最低,4种方案中第四种精度最低。
3.3 短边GPS点坐标与三等导线点坐标的对比分析
把网平差的坐标与三等导线点坐标进行比较,求其坐标差,分析各种网形、各种方案的精度。
根据中误差公式[见式(21)]计算a网形各种方案的坐标较差中误差,结果如图3(a)所示。用同样的方法计算b、c、d网形的坐标较差中误差,结果如图3(b)、图3(c)、图3(d)所示。
由短边GPS点坐标与三等导线点坐标对比分析知,每种网形中第二种方案精度高于第一种方案,第三种方案精度高于第四种方案,即网形内的已知点数量相同时,已知点间的距离或者已知点构成的图形的面积越大,点位精度越高。
4 讨论与结论
通过GPS网形指标、坐标较差以及GPS点坐标与三等导线点坐标的对比分析,可以得出如下结论。
①c网形精度最高,能达到《工程测量规范》(GB 50026—2007)三等精度指标;a网形和d网形精度次之,能达到一级精度指标;b网形的精度最低,仅能达到二级精度指标。
②4种网形内第三种方案精度最高,第四种方案精度最低,两种方案均有三个已知数据。增加已知点数量对精度有何种影响取决于已知点在网形的分布。
③已知点数量相同位置不同时,已知点间的距离越长或者已知点构成的图形面积占整个网面积的比例越大时,网的精度越高。布设GPS点时,点的周围有树木或高压线均会使网的精度降低。
④比较得出的短边GPS网精度指标,查阅相关测量规范知4种网形均适用于地形测量、地籍测量、土地测量、建筑施工测量、水利施工测量、土地整理、土地确权。综上,一般工程均可采用短边GPS控制网,仅少数精度要求较高的安装工程或大坝变形监测工程不适用。
参考文献:
[1]丁明华,余存林,郭秉程.GPS工程控制网的布设[J].西部资源,2012(4):168-171.
[2]谢钢.全球导航卫星系统原理:GPS、格洛纳斯和伽利略系统[M].北京:电子工业出版社,2013.
[3]徐绍铨,张华海,杨志强.GPS测量原理及应用[M].武汉:武汉大学出版社,2008.
[4]修涛,张琦.GPS控制网布设与解析[J].露天采矿技术,2013(1):45-47.
[5]王天仓,张照杰,李月宝,等.GPS控制网的布设原则及优化设计探讨[J].测绘通报,2009(6):28-31.
[6]刘钰.工程测量中GPS控制测量平面与高程精度分析[J].建材与装饰,2018(15):219.
[7]王于.工程测量中GPS控制测量平面与高程精度分析[J].居业,2016(10):31,33.
[8]穆宁.工程测量中GPS控制测量平面与高程精度分析[J].低碳世界,2016(26):115-116.
[9]唐凯.邻水县GNSS控制测量及高程拟合研究[D].成都:成都理工大学,2016.
[10]郝伟涛.省域D、E级GNSS加密控制网设计与实现[D].郑州:解放军信息工程大学,2015.
[11]冯长青.GPS控制网观测方案的优化[J].辽宁科技学院学报,2011(3):36-38.
[12]李征航,黄劲松.GPS测量与数据处理[M].武汉:武汉大学出版社,2016.
[13]冮宏军,李春华.静态GNSS控制网三维无约束平差及精度分析[J].北京测绘,2015(1):47-49.
[14]王忠礼,顾刘丹,姬前锋.MATLAB软件支持下的GPS基线向量网的三维无约束平差[J].北京测绘,2014(1):79-83.
[15]刘大杰,白征东.一种GPS网三维平差的数学模型[J].测绘学报,1997(1):39-43,73.

