基于遗传算法的突发公交智能调度算法

徐晨畅　钱松荣

摘 要： 公交车是城市交通的重要工具，为了优化乘客等车时间，同时使额外成本保持在可以接受的范围内，提出一种应对突发交通状况的公交智能调度算法，在突发状况下派遣公交车支援合适站点。通过结合实际场景设计调度方案，给出方案的数学模型和优化问题，基于遗传算法，求解出合适的公交车支援方案。采用某地的实际道路交通和公交数据，对算法进行了仿真，结果表明，提出的算法能够有效的给出公交调度建议。

关键词： 公交调度; 智能调度; 遗传算法

中图分类号： TP 311文献标志码： A

Intelligent Bus Dispatch Algorithm for Emergency Based on Genetic Algorithm

XU Chenchang， QIAN Songrong

（

School of Information Science and Technology， Fudan University， Shanghai 200433， China

）

Abstract： Bus is one of the most important vehicles of city transportation. In order to reduce the waiting time of the passengers and make extra cost controlable for the bus company， an intelligent bus dispatch algorithm for emergency is proposed. It designs a new mathematical model to describe the dispatch problem and provides a method based on Genetic Algorithm to calculate the best dispatch scheme. With the real transportation data of a certain city， the algorithm is proved to be effective in simulation.

Key words： bus dispatch; intelligent dispatch; genetic algorithm

0 引言

随着城市的快速发展，城市交通需求越来越密集，越来越多的人采用公共交通出行。公交车，作为一种传统的公共交通工具，在城市交通中扮演十分重要的角色。由于交通情况非常复杂且难以预测，人为的制定公交车的发车时间和发车间隔越来越难以满足乘客的需求，常常出现乘客花大量时间等候公交车，或是公交车接连到站，导致资源的浪费。

近年来，随着物联网的发展，公交车已经不再是孤立的个体。公交公司可以通过网络和嵌入式设备，实时获取公交车的坐标位置和上下车乘客数量;通过大数据分析，可以实时计算道路交通情况。基于此，人们开始尝试优化公交车的调度问题。

崔明月[1]等提出基于历史数据，使用遗传算法取代人为分析，为公交车一天中的各个时间段计算出不同的发车间隔。郑思瑶[2]提出越站实时调度模型，即在满足下车乘客正常下车的前提下，公交车选择性的进行停站，使整个公交运行效率更高，乘客乘车时间更短。

本文提出，在道路发生堵车、交通事故等突发情况时，拥挤路段前方的乘客需要等待大量时间才能上车，在此种情况下，使用一种智能算法，自动从合适的站点调用合适的空车支援拥堵路段前方车辆，在尽可能少增加公交公司运行成本的条件下，尽可能减少乘客的等车时间，优化乘车体验。下文将给出算法模型、模型解法和实验分析。

1 调度模型

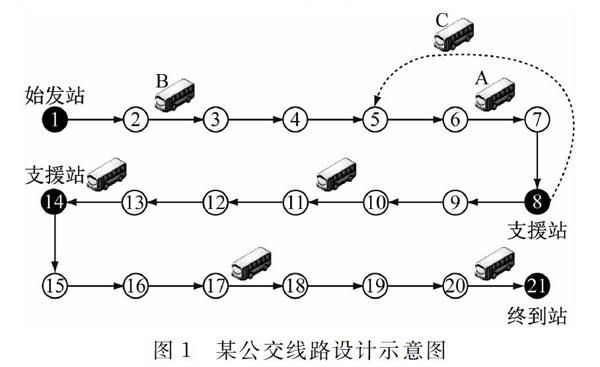
将某条公交线路，如图1所示。

图1中标有序号的圆圈为线路上的21个站点，其中，实心圆圈代表蓄车站（始发站、终点站、支援站），可以提供车辆支援，除C以外的公交车为当前在线路上运行的公交车。假设站点4和站点5之间发生交通拥堵，站点5及其后续站点的乘客将等待大量时间才能够坐上公交车，此时，若站点8与站点5之间有较为通常的道路，可从站点8派遣车辆直达站点5加入运行线路，将能够有效减少乘客等车时间。

针对多条线路的情况，如图2所示。

共有3条公交线路，在此条件下，实心的蓄车站被设计为可以支援任何一条线路的任何站点。

将此问题描述为一个优化问题，有以下假设：

（1） 公交车在每两个站点之间匀速运行;

（2） 公交车到达每个站点后，能够满足所有上车需求;

（3） 是否加入新的公交车不影响站点乘客到达率;

（4） 支援公交车加入后，在可预期的未来，路况保持平稳。

已知固定量有：

（1） 线路l每两个站点之间的距离d1（l，i，j）;

（2） 线路l的站点数N（l）;

（3） 蓄车站m前往线路l的站点n距离d2（l，m，n）;

（4） 单位时间等效成本（基于城市平均工资）ρ;

（5） 公交车停站耗时τ;

（6） 公交车停站成本c1;

（7） 公交车单位距离油耗c2。

已知实时量有：

（1） 线路l上公交车的位置集合bi;

（2） 线路l上每两个站点之间的运行时间t1（l，i，j）;

（3） 蓄車站m前往线路l的站点n所需时间t2（l，m，n）;

（4） 线路l的站点k乘客到达率（基于历史数据计算）σ（l，k）。

自变量有：

（1） 派遣支援车辆的出发站点a;

（2） 派遣的目标线路和站点（L，b）;

应变量是：

加入新支援公交车后，节省的成本C（减少的时间成本和增加的运营成本总和）。

优化目标是：

使C最大化的若干种自变量取值。

其中，应变量C可由式（1）求得如式（1）。

其中，以图1为例，T1表示未加入公交车C之前，公交车A和公交车B之间站点的乘客等车时间，设

bL（A）

设tAB为A、B两辆公交车的时间间隔，tA（k），tB（k）分别为公交车A、B与站点k的时间间隔，T1由式（4）得到式（4）。

T2表示加入公交车C之后，公交车A和公交车B之间站点的乘客等车时间总和，其表达式如公式（5）所示，其中，tc（k）表示站点k与公交车C的时间间隔。

T3表示新加入公交车所需的运营人员（如司机）增加的工作时间，如式（6）。

C4表示新加入公交车所增加的停站成本、油耗成本等，如式（7）。

从而，我们建立了智能调度算法的调度模型。

2 模型求解

使用遗传算法[3]可对第1部分的优化问题进行求解，求解流程如下：

（1） 染色体初始化

以图2情况为例，蓄车站共有7个，用3位二进制数

a表示，目标线路总共有3条，用2位二进制数L表示，最长的线路共有23个站点，所以需要用5位二进制数b表示。可见，一个支援方案的变量共需用10位二进制数表示。在一个大的公交系统中，我们希望一次求解能够同时获得对不同路段的多个支援方案，定义方案上限为M个，如M为10时，则总共需要100位二进制数表示这10个方案。这100位二进制数，就是遗传算法中的一个染色体。在遗传算法中，还需定义种群大小P，如当P为200时，在初始化的过程中，需要随机初始化200组长度为100的染色体（chain）。随机初始化的结果需要根据约束条件判断是否有意义，本模型的约束条件包括：

（a） 各变量在约束范围内，1≤a≤7，1≤L≤3，1≤b≤N，其中N为线路L的站点数;

（b） 保证每两辆正在运行的公交车之间，最多加入1辆支援车辆。

（2） 计算适应度

对当前的P组染色体，分别计算节省的成本C，代入sigmoid函数中求出适应度F，如式（8）。

其中，θ为根据实际情况定义的一个常数，尽可能使使C/θ的取值在sigmoid函数的非饱和区。此时，还需保留一个使F最大的最佳染色体bestchain。

（3） 自然选择

根据每个染色体的适应度，采用轮盘赌的方式选择出P个子代染色体。

（4） 交叉

设每条染色体的每一个支援方案为染色体的一个片段，将P个染色体两两配对，交换两个染色体的随机一个片段，若交换后，两条染色体仍满足约束条件，则完成交换，若不满足约束条件，则撤销交换。

（5） 变异

对每条染色体的每个二进制数以Pm的概率取反，增加种群多样性。变异后，验证各染色体是否满足约束条件，若不满足，则撤销变异。

（6） 精英保留

为了保证最佳染色体不在上述过程中消失，完成上述过程后，随机将P个染色体中的一个替换成bestchain。

设最大代数为MaxGen，在达到最大代数之前，循环执行步骤2）至步骤6），最终bestchain会趋于最优解，排除bestchain的M个方案中使C<0的方案，剩余的方案即为最优（近似）调度方案的组合。

3 实验仿真

本文主要目的是验证算法的可行性，采用Matlab对本实验的模型和算法进行了仿真。如图3所示。

某地区的三条线路（701、702、713），三角形标识的为蓄车站。

在该仿真问题中，设定M为10，染色体长度为110，P为200，MaxGen为300。站点间、各蓄车站到各站点的路程为在某地图软件量取的真实路程;站点间、各蓄车站前往各站点的运行时间采用某时刻地图软件基于大数据给出的机动车运行时间估计;运行车辆分布根据公交公司网站查询的发车间隔，结合站点间机动车运行时间数据人为设定;乘客到达率根据站点所处地段估测得到。另外，根据当地人均收入，以每日工作8小时为标准，计算出ρ=0.15 yuan/min。τ、c1、c2根据实际情况给出。

如上文描述，仿真中的大部分数据来源如线路、路程、运行时间、ρ等是真实数据;少部分无法获得真实数据的，如乘客到达率人为设定，设定过程中尽可能反应真实情况。因此，使用这些数据，能够有效模拟真实场景，仿真结果具有实际意义。

仿真案例中，所有站点序号从北往南，从小到大，从1开始标记。人为增加701线路11～12站点间运行时间，702线路14～15站点间运行时间，713线路17～18站点运行时间后，用于模拟这3个路段发生交通拥堵，在此种情况下，验证算法的正确性。仿真过程如图4所示。

可以看出，随着迭代不断进行，bestchain的节省的成本C不断增加，最终结果为359.5元。在这个结果下给出的方案是：

（1） 从蓄车站2派出一辆车前往701线路的12站点;

（2） 从蓄车站5派出一辆车前往702线路的16站点;

（3） 从蓄车站5派出一辆车前往713线路的18站点。

其中，蓄车站2为图3中左上方的三角形标注的站点，蓄车站5为图3中心的三角形标注的站点。可以看出，通过模型的求解，派遣蓄车站的车辆支援拥堵路段的后续站点，降低了时间成本，从而降低了整体的成本，符合直观的认知。由此可见本文提出的模型和求解方法能够给出合理的调度支援方案。

4 总结

本文基于公交实时位置信息和乘客到达率信息，对突发公交智能调度的场景进行建模，利用遗传算法进行求解，实现了在道路部分拥堵时的一种有效的调度算法。通过实验可以看出，算法能够准确的计算出合适的支援车辆所在蓄车站和合适的目标站点。本文所述方法，能够一定程度解放城市公交调度中所需的人力，为解决城市公交调度问题提供了一种有效的智能解决方案，也是公交调度平台软件开发的可行参考。

参考文献

[1] 崔明月，黄荣杰，刘红钊，等.量子遗传算法在公交车辆调度中的应用[J].实验室研究与探索，2014，33（12）：72-76.

[2] 郑思瑶. 车车通信条件下的公交实时调度方法研究[D].北京：北京交通大学，2016.

[3] 葛继科，邱玉辉，吴春明，等.遗传算法研究综述[J].计算机应用研究，2008（10）：2911-2916.

（收稿日期： 2019.06.09）

作者簡介：

徐晨畅（1994-），男，硕士，研究方向：数据通信与网络。

钱松荣（1963-），男，硕士，教授，研究方向：数据通信与网络。