基于偏Laplace正态数据下位置、均值回归模型的参数估计

郑桂芬,吴刘仓,聂兴锋

(昆明理工大学理学院,云南 昆明650093)

1.引言

在金融、医学和社会经济领域中,存在大量偏斜且厚尾的数据.如果用正态分布、偏正态和偏t分布去拟合,得到的信息不精确,利用偏Laplace正态分布对数据进行拟合获得的信息更具有准确性和可靠性,因此研究偏Laplace正态分布具有重要意义.

在过去几十年里,学者们提出很多方法分析处理偏态数据.Azzalini[1]提出了偏态指数幂分布同时处理偏态和重尾两种情况;Monti[2]对偏态指数幂分布性质和推断进行了研究;WU等[3]利用联合惩罚似然方法对偏正态分布下联合位置与尺度模型提出了一种可行有效的变量选择方法;吴刘仓等[4]研究了偏正态数据下联合位置与尺度混合专家回归模型的参数估计;马婷等[5],吴刘仓等[6]分别基于SN,StN分布下研究了联合位置、尺度与偏度模型的极大似然估计.偏正态分布的概率密度由差的平方进行刻画,为了能使估计的结果更加具有稳健性,把偏正态分布进行扩展,从而引入偏Laplace正态分布,其概率密度用差的绝对值来表示.因此,分布的尾部比正态分布更加平坦.由于偏Laplace正态分布受异常点数据的影响不大、得到的结果比较稳健,吸引了很多学者的研究兴趣.Dogru和Arslan[7]在偏Laplace正态分布下研究了混合回归模型的参数估计.Garay等[8]研究了偏正态分布混合尺度的非线性回归模型的统计诊断.张舒宇等[9]研究了基于Laplace分布下混合联合位置与尺度模型的参数估计.

综上所述,虽然偏Laplace正态分布的回归模型已经有很多研究成果,但在偏Laplace正态分布下对位置和均值回归模型建模的涉及较少,考虑到位置和均值建模的重要性,本文详细介绍了利用EM算法对这两个模型的参数进行极大似然估计,并通过实例结果表明本文所提出来的模型和方法的实用性和可行性.

本文结构安排如下: 第二部分给出了偏Laplace正态分布的一些性质;第三部分给出了偏Laplace正态分布下位置和均值回归模型;第四部分利用EM算法对位置和均值回归模型的参数进行极大似然估计;第五部分通过Monte Carlo随机模拟实验证实了本文提出方法的有效性;最后,实例研究结果表明,本文所提出的模型和方法是科学合理的.

2.偏Laplace正态分布

对于服从偏Laplace正态分布的随机变量Y可以表示为Y ∼SLN(µ,σ2,λ),其中µ为位置参数,σ2为尺度参数,λ为偏度参数.则其概率密度函数可表示为

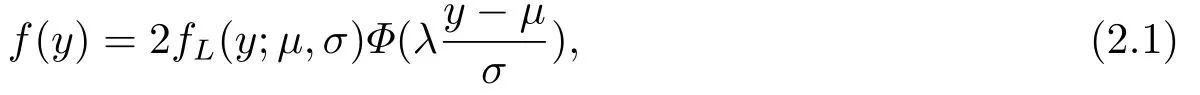
其中Φ为标准正态分布的分布函数,fL(y;µ,σ)为Laplace分布的概率密度函数,且

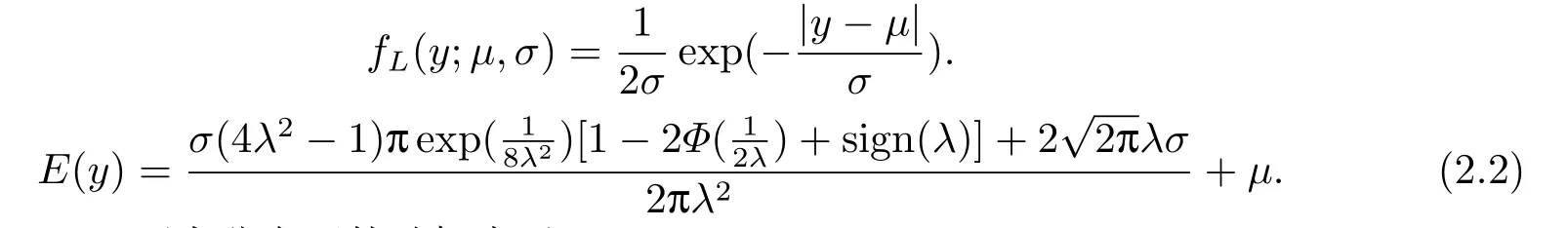
Ⅰ偏Laplace正态分布下的随机表示

设Z ∼SN(0,1,λ),V的概率密度函数为fV(v) =v−3exp(−(2v2)−1),v >0是两个独立随机变量,随机变量Y ∼SLN(µ,σ2,λ)表达式为

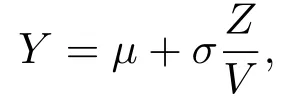
然后,利用文[1]中的201页和文[10]中的定理1,分布随机变量Z的随机表示得随机变量Y的以下随机表示

其中Z1∼N(0,1),Z2∼N(0,1)是独立随机变量,从而得到偏Laplace正态分布的层次表示

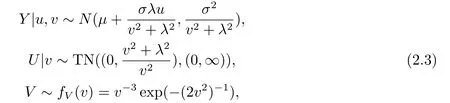
3.位置和均值回归模型

Ⅰ位置回归模型

由概率密度函数式(2.1)及位置参数回归模型(3.1)可以得到

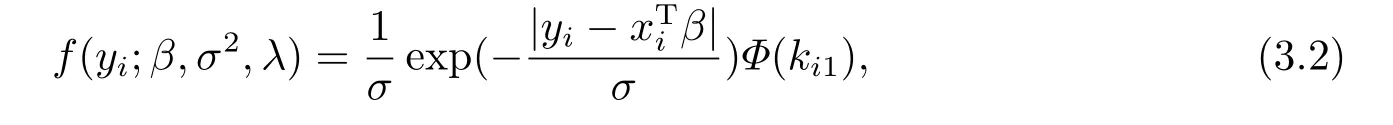
Ⅱ均值回归模型

这里yi为第i个响应变量,服从位置参数为µi,尺度参数为σ2,偏度参数为λ的偏Laplace正态分布,xi=(xi1,··· ,xip)T是解释变量,β=(β1,··· ,βp)T是维数为p×1的位置回归模型的未知参数,α=(α1,··· ,αp)T是维数为p×1的均值回归模型的未知参数.

本文采用极大似然估计的方法对参数进行估计,但因有潜变量存在,所以直接估计参数比较困难.EM算法作为解决潜变量问题参数估计的有效方法,因此接下来本文介绍所提出模型参数的极大似然估计的EM算法.

4.极大似然估计的EM算法

Ⅰ位置回归模型下极大似然估计的EM算法

由式(3.2)可得似然函数为:

EM算法(Expectation Maximization Algorithm)是一种迭代算法,其具体流程分为两个步骤进行: E-step是根据参数初始值或上一次迭代所得结果来计算对数似然函数的期望值;M-step是将对数似然函数最大化以获得新的参数值,用新得到的参数值代替初始值或上一次迭代所得结果使得对数似然函数最大化.重复执行以上两步骤,直至收敛.下面给出EM算法在偏Laplace正态数据下位置回归模型的参数估计中的计算步骤:

E-step: 给定观测数和当前参数值,求出(4.3)式中给出的完全数据似然函数的条件期望,即计算(4.5)-(4.7)式中的条件期望.

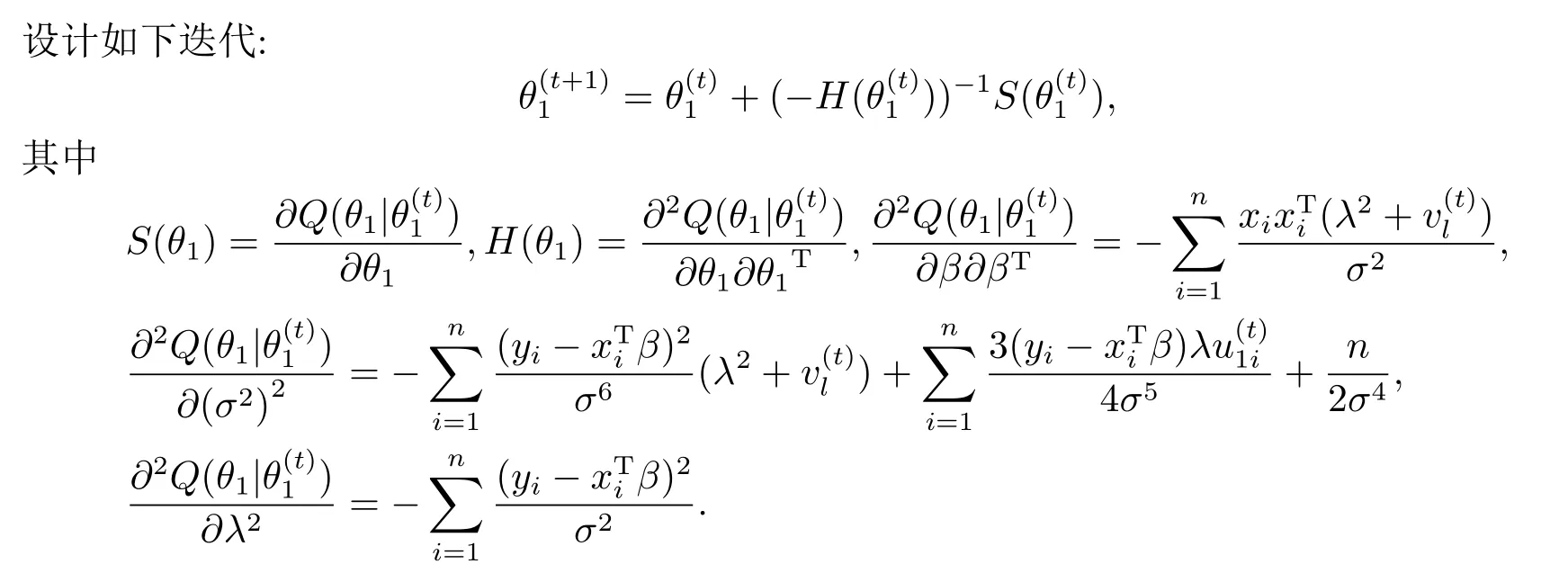
Ⅱ均值回归模型下极大似然估计的EM算法

由式(3.4)可得似然函数为

设u=(u1,··· ,un),v=(v1,··· ,vn)为缺失数据,(y,u,v)为完全数据.然后用层次表示法得完全数据下对数似然函数为

下面给出EM算法在偏Laplace正态数据下均值回归模型的参数估计中的计算步骤：

E-step: 给定观测数据和当前参数值,求出式(4.11)中给出的完全数据似然函数的条件期望,即计算(4.13)-(4.15)中的条件期望.

5.Monte Carlo模拟

Ⅰ位置回归模型参数估计的Monte Carlo模拟

为评价位置回归模型参数估计方法的有效性,本文对有限样本进行模拟研究,参数估计的精确度使用均方误差(MSE)来评价和衡量,其定义如下:

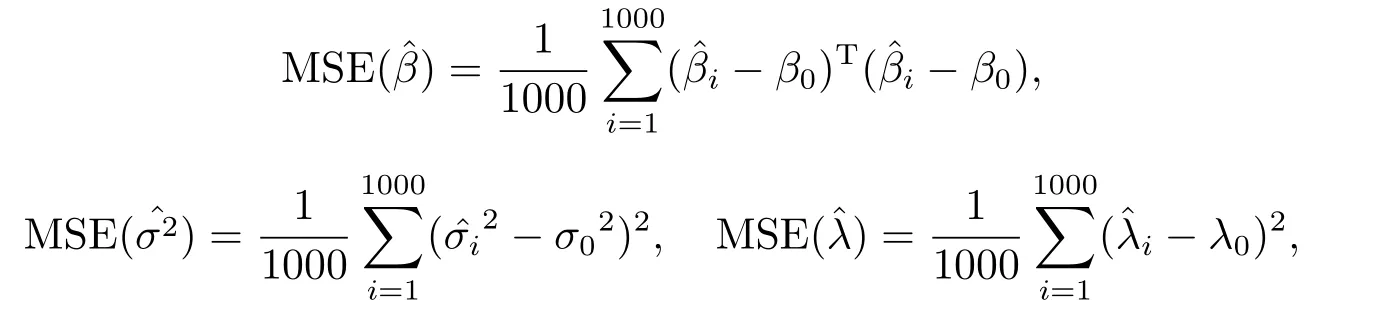
根据模型(5.1)产生模拟数据,其中xi ∼U(−1,1).yi(i=1,2,··· ,n)是根据偏Laplace正态分布产生的响应变量,且yi服从偏Laplace正态分布,yi的产生过程如下:

1) 样本U来自均匀分布(0,1)并设;

2) 样本Z1和Z2独立于标准正态分布N(0,1);

3) 用适当的参数值给出偏Laplace正态分布样本.

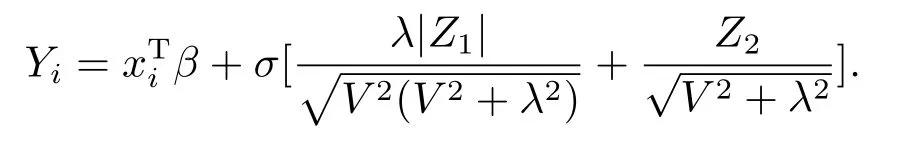
Ⅱ均值回归模型参数估计的Monte Carlo模拟

为评价均值回归模型参数估计方法的有效性,参数估计的精确度使用均方误差(MSE)来评价和衡量,其定义如下:

均取样本量n=50,100,150,200,重复模拟1000次.模拟结果见表1、表2.

表1 位置回归模型的参数估计模拟结果

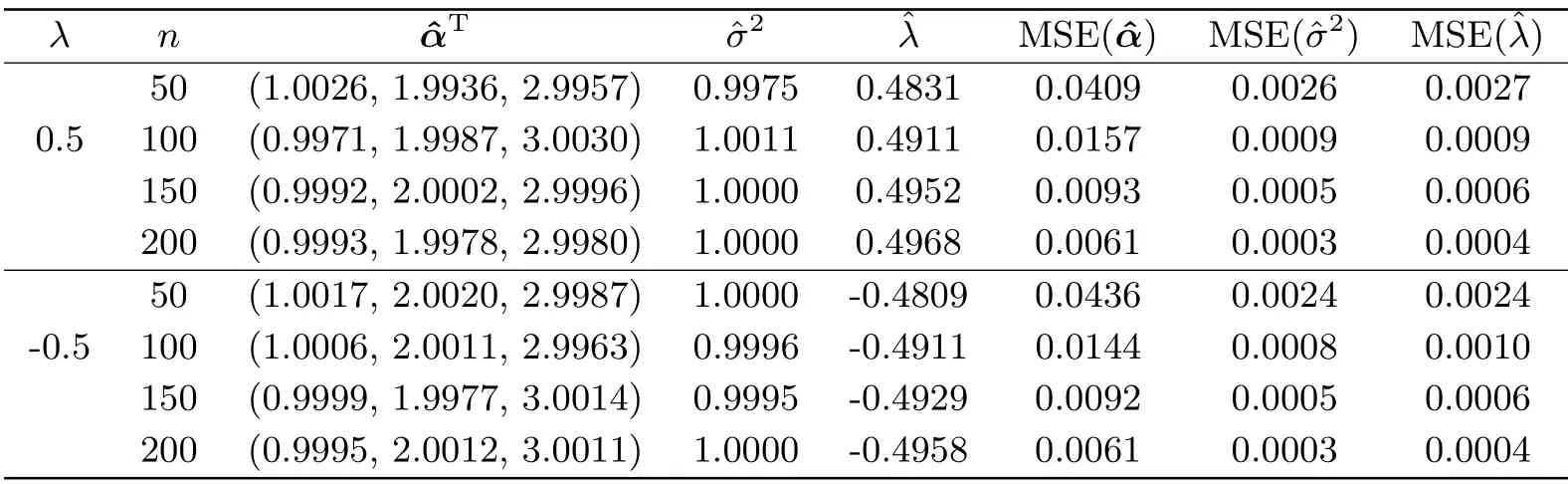
表2 均值回归模型的参数估计模拟结果(由于λ在分母上,故λ≠0)

从表1和表2可以得到,随着样本量n的增大,所有数的估计值越来越接近真值,而且估计的均方误差(MSE)也越来越小.以上结论表明,本文提出的偏Laplace正态数据下位置和均值回归模型及所使用的EM算法对参数的极大似然估计取得了较理想的效果.

6.实例分析

近年来,随着人们收入的增长和生活水平的提高,观看电影逐渐成为人们消遣娱乐的一种方式,故电影行业发展迅速,下面利用本文提出的偏Laplace正态分布的位置和均值回归模型及其方法,对电影票房数据进行参数估计.本文对收集到的各类电影总票房和首映票房进行统计分析,该数据中包含一个响应变量Y-总票房和一个解释变量X-首映票房,计算可得电影总票房的偏度系数结果表明是右偏的,直方图如图1所示.

图1 电影票房数据分布直方图

图1和偏度系数说明电影票房数据近似的服从偏Laplace正态分布,所以可以利用该数据对偏Laplace正态分布的位置和均值回归模型做参数估计,考虑Y与X之间的模型如下:

利用第四部分提出的参数估计方法,得到下表3.

表3 电影票房数据的位置、均值回归模型参数估计结果

由于在同一组电影票房数据中,尺度和偏度参数是一样的.从表中可以看出在两个模型中的σ2和λ大体相同,但β和α在模型中代表了不同的位置,所以存在较大差异,与实际相符合,表明我们提出的模型和方法是科学合理的.

7.结论

本文利用EM算法研究了偏Laplace正态数据下位置和均值回归模型的参数估计.从Monte Carlo模拟结果来看,本文提出的EM算法对位置和均值回归模型的参数估计取得了较好的效果,并且在实例分析中,对电影票房实际数据的应用研究也表明了本文提出的模型和方法是科学合理的.