淮河流域渠北地区降水年内分配特征研究

闫中月，陆小明，徐 静*

（1.南京大学 表生地球化学教育部重点实验室，南京 210023；2.南京大学 地球科学与工程学院，南京 210023；3.江苏省水文水资源勘测局，南京 210029）

降水年内分配特征是降水的时间结构，表征降水年内过程形态[1]，决定着区域水资源的天然配置，同时对地区植被格局及生态环境有着深刻的影响。因此，降水年内分配是防洪工程规划和布局、水资源配置和水环境容量设计必须考虑的因素，一直以来是水文水资源学研究的热点。近年来，已有学者在蚂蝗田小流域[2]、清江流域[3]、黑河流域[1]、太湖流域[4]、砚瓦川流域[5]和大汶河流域[6]等不同流域及北京市[7]、河南省[8]、长江源区[9]、祁连山地区[10]、中国东南沿海地区[11]、东北地区[12]、青藏高原[13]和南亚地区[14]等不同地区开展了降水年内分配不均匀性研究。这些研究通常采用不均匀系数、集中度和集中期等指标表征降水年内分配特征，同时常用Mann-Kendall（M-K）检验法、距平累积法和线性回归法[15]等检验方法开展趋势分析。然而，当前研究多是从时间角度分析某地区降水年内分配不均匀性的趋势，并未分析降水分配特征随不同降水年型变化的趋势，也未对年内降水不均匀性差异的原因进行剖析。而降水年型是进行水利工程设计、水资源配置和水环境容量计算的重要水文条件。不同降水年型降水年内分配特征影响着水利工程设计规模、水资源优化配置和水环境管理策略的制定。因此，本文采用常用的不均匀系数、集中度和集中期等降水年内分配指标分析淮河流域渠北地区降水年际变化趋势，开展不同降水年型年内分配特征研究，并进一步分析造成年内分布均匀性差异的原因，以期为本区域水资源合理配置、水环境容量管理提供理论依据。

1 数据与方法

1.1 研究数据

本文采用淮河流域四级水文分区——渠北地区内及邻近的高良涧闸、淮阴、朱码闸、阜宁、滨海和翻身河闸6个站点1956—2017年逐月降水数据。各站年降水量特征统计见表1。由表1可知，该地区多年平均降水量为891.7～988.7 mm，标准差为197.3～226.6 mm，最大年降水量为最小年降水量的2.65～3.32倍。

表1 渠北地区六站点年降水量统计表Table 1 Statistics of annual precipitation at six stations in Qubei area

1.2 研究方法

1.2.1 年内分配分析方法

年内分配不均匀系数Cv表征年内降水分布的不均匀性，定义为年内月降水量标准差与平均值之比。其计算公式为：

式中：Ri为年内第i月降水量。Cv值越大，年内各月降水量相差越大，降水年内分配越不均匀。

集中度表示年内月降水集中程度，集中期表示降水重心所在时刻[16-17]，计算公式如下：

式中：Cd为集中度，其值代表年内降水集中程度，如降水量全部集中在某一月份时，集中度为1，降水量均匀分布时，集中度为0；D为集中期，表示年内降水重心所在时刻；Ri为年内第i月降水量；θi为第i月的向量角度，1—12月的向量角度分别定义为0°～330°，每月间隔为30°。

1.2.2 年际变化分析方法

Mann-Kendall（M-K）法能够定量识别连续时间序列的变化趋势及显著性水平，通常应用于水文、气象时间序列变化趋势和突变分析[18-21]。假设某一长度为n的时间序列为X={x1,x2,…,xn}，变化趋势倾向度β值[22]和趋势显著性水平统计量Z值[23]计算公式如下：

式中：xi，xj分别为时间序列X的第i、j时刻的样本值；n为样本总量；S为样本统计量，定义如下：

式中：sgn（θ）为符号函数，定义如下：

在突变分析中，通过绘制Mann-kendall法的UF和UB统计量曲线图，判断是否存在显著突变，UF计算公式如下：

UB的计算方法与UF一致，但其计算序列为原时间序列逆序列。假设统计量Z、UF和UB符合正态分布，显著水平取0.05，则相应显著性临界值为±1.96[8，24]。

线性回归法采用一元线性回归方程分析时间序列变化趋势，其计算公式可以表示为

式中：X、T均为时间序列；a为回归系数，表征线性倾向率；b为回归常数。

2 结果与讨论

2.1 降水年内分配特征年际变化分析

渠北地区各站点1956—2017年年内降水分配不均匀系数、集中度和集中期的变化如图1所示。从图1可以看出，不均匀系数、集中度和集中期均随时间波动；各指标的最值出现年份既有部分一致性又存在一定差异，如朱码闸、阜宁、滨海站不均匀系数最小值出现在1967年，而高良涧闸、淮阴和翻身河闸不均匀系数最小值分别出现在1959年、1966年和1976年。

采用M-K方法分析渠北地区各站点降水年内分配指标年际变化趋势，结果如表2所示。从表2中倾向度β可以看出，除翻身河闸外，其余各站不均匀系数均为负值，表征渠北地区年内分配不均匀性总体有降低趋势；高良涧闸和翻身河闸集中度为正值，其余各站为负值，表征各站年内降水集中程度年际变化趋势并不一致；各站集中期均为正值，表征降水集中时期有后移趋势。虽各指标存在一定的趋势，但变化幅度均不大，不均匀系数、集中度变化率均小于0.01/10 a，集中期变化率小于1.29°/10 a（约0.04月/10 a）。从统计量Z来看，在显著水平为0.05时，各指标变化趋势均不显著。

采用M-K突变分析方法进一步绘制各站降水年内分配特征指标UF和UB曲线以判断是否发生突变。结果显示，各站不均匀系数、集中度、集中期的UF、UB统计量均存在多个交叉点，表明各站年内降水分配特征各指标可能存在多个突变点，但UF和UB统计量除个别年份外均在置信区间（-1.96，1.96）之内，即突变点前后变化趋势均未突破显著性临界值，故各指标突变均不显著，图2展示了高良涧闸、淮阴和朱码闸站点的UF和UB统计结果。

图1 降水年内分配指标变化Fig.1 Variation of intra-annual precipitation distribution indices

表2 降水年内分配指标M-K趋势检验Table 2 M-K trend test of intra-annual precipitation distribution indices

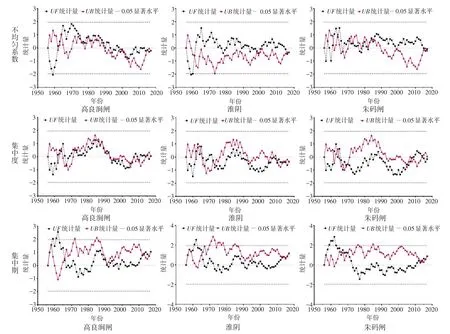
图2 降水年内分配指标M-K突变分析Fig.2 M-K mutation analysis of intra-annual precipitation distribution indices

2.2 不同降水年型年内分配指标变化分析

为分析不同降水年型年内分配指标变化趋势，采用《水文情报预报规范》（GB/T 22482—2008）中的要素距平值划分降水年型（表3），进行了不同降水年型年内分配指标均值和标准差的线性趋势拟合。结果显示，各站点的不均匀系数和集中度线性趋势拟合优度R2均在0.5以上，且其线性倾向率均为正值，不均匀系数的线性倾向率为0.05～0.09，集中度的线性倾向率为0.03～0.05，表明不均匀系数和集中度总体呈现出随降水年型变丰而增大的趋势，丰水年较枯水年份降水具有更大的不均匀性。但各站点集中期线性趋势拟合优度R2均在0.3以下，拟合优度不高，线性趋势不够明显，表明降水的年内重心是一种波动状态，并未有随降水年型变化而线性变化的规律，图3展示了高良涧闸、淮阴和朱码闸站点的拟合结果。

表3 丰平枯年型划分标准Table 3 Classification criteria for wet,normal and dry years

图3 不同降水年型年内分配指数Fig.3 Intra-annual precipitation distribution indices in different precipitation years

2.3 不同降水年型年内分配指标变化成因分析

为分析不同降水年型年内分配指标变化的原因，统计了不同降水年型各站月降水量及其占比的均值。不同降水年型月降水量均值分布如图4所示。从图4可以看出，渠北地区各站不同年型降水量在1—9月总体存在随降水年型变丰而增加的趋势，特别是6—9月往往存在较大的改变，而10—12月这种趋势并不明显，其变化无特定规律。

不同降水年型月降水量占比均值分布如图5所示。从图5可以看出，降水占比随年型变化趋势未有降水量的变化趋势明显，对于降水量随降水年型变丰增加的1—9月，其1—5月降水占比整体上随降水年型变丰呈现降低的趋势，而6—9月降水占比并未呈现出规律性；对于降水量变化趋势不明显的10—12月，其降水占比整体随降水年型变丰而降低。因此，可以得出随着降水年型变丰，降水量1—9月呈现出比较一致的增长趋势，而10—12月变化无规律，降水占比1—5月和10—12月均呈现降低趋势，6—9月的变化无规律，但6—9月降水占比总和存在增大趋势。

因此，降水年型变丰的主要原因在于1—9月降水量的增加，特别是6—9月降水量的增大。而降水年变丰不均匀系数增大的原因在于随着降水年型变丰，1—5月和10—12月的降水占比降低，6—9月降水占比总和增加，使降水更加集中于6—9月。但由于6—9月单个月份的降水占比并未呈现出随年型变化的趋势，使得年内降水重心的变化在不同年型的分布并不规则，未有显著趋势。

图4 不同降水年型各站月降水量Fig.4 Monthly precipitation of each station in different precipitation years

3 结论

1）渠北地区1956—2017年降水年内分配指标总体上随时间波动变化。不均匀系数和集中度有降低趋势，集中期有后延趋势，但未通过显著性检验，且变化幅度较小，不均匀系数、集中度的趋势变化率不足0.01/10 a，集中期的趋势变化率小于1.29°/10 a，各指标均未出现显著突变。

2）渠北地区降水年内分配不均匀系数和集中度总体表现出随降水年型变丰而增加的趋势，丰水年具有更大的不均性；集中期未表现出随降水年型变化而线性变化的趋势。

图5 不同降水年型各站月降水占比均值分布Fig.5 Mean distribution of monthly precipitation at each station in different precipitation years

（3）渠北地区年内分配不均匀性随降水年型变化的原因主要在于随着降水年型变丰1—5月和10—12月的降水占比降低，6—9月降水占比总和增加，使降水更加集中于6—9月，而集中期并未有随降水年型变化而线性变化的原因是6—9月单个月份的降水占比并未随年型变化表现出线性趋势。