不规则波作用下排桩式透空堤透浪系数试验研究

黄健钧，于 倩，陈国平，严士常

(1.河海大学 海岸灾害及防护教育部重点实验室，南京 210098；2.河海大学 港口海岸与近海工程学院，南京 210098)

防波堤的主要作用是阻挡海外波浪的传播以减小港内波高，让港内船舶达到泊稳要求进行装卸作业。随着环境保护的要求越来越高，实心式防波堤的使用受到了限制。透空式防波堤由于较小的结构自重，同时具有节省材料又利于港内外水沙在下部空间的自由交换，可以有效防止港内淤积的优点，其结构形式已经成为更多港口工程的首选。较为常见的透空堤形式包括：排桩式透空堤、桩基挡板式透空堤、多层挡板式透空堤和梳式透空堤等[1]。随着近些年防波堤施工技术的进步和波浪理论的愈发成熟，透空堤具有十分广阔的应用前景。

透浪系数是防波堤最为关键的参数指标，其物理含义系堤后透射波高与堤前入射波高之比，反映了防波堤的消浪能力。关于实心堤、潜堤等结构形式的透浪系数，前人已经进行了较多的研究[2-6]。而在透空堤方面，国内外的学者主要用理论推导、物理模型试验和数值模拟三种手段进行分析研究。对于排桩式透空堤，1961年Wiegel首次分析了波浪与小间距桩基透空堤的相互作用，认为波浪的透射系数仅与桩间距有关，并提出了相关计算式[7]。在Wiegel的基础上，1969年Hartmalm和1976年Massel分别考虑了入射波浪的能量和入射波浪的散射，给出了另外两个理论解[8-9]。但是上述的理论推导都假定波浪的透射系数仅与桩间距有关，为了综合考虑桩间距和波要素等对透射系数的影响，一系列学者进行了物理模型试验。1966年Hayashi进行了二维水槽试验，发现波浪的透射系数与桩间距有明显的关系，受堤前水深的影响较小[10]。同年Nagai通过物理试验，提出了桩顶高程对桩式防波堤的消浪性能有显著的影响，桩顶的越浪会明显增大透空堤的透射系数[11]。基于单排桩透空堤的研究，1988年Herbihc和Douglas进一步研究了双排桩透空堤的消浪特性，得出透浪系数随波高增大而减小，随周期增大而增大的结论[12]。2006年Huang通过一排和双排小间距矩型桩结构的波浪试验，同样得出了透浪系数随波高增大而减小的规律特性，同时发现了前后排桩的间距对透浪系数影响不大[13]。随着施工技术的发展，更大尺寸的桩结构也得到使用，2015年刘晨通过物理模型试验，发现了大直径圆筒结构的透浪系数主要受到桩间距、波陡和结构超高的影响，并在Hartmalm公式基础上拟合出大直径圆筒透射系数的计算公式[14]。

基于前人的分析研究，排桩式透空堤在国内上海[15]和国外西非[16]等地方也得到了实际应用。然而，目前来说对于排桩式透空堤的分析研究还不够透彻，特别是在三维波浪环境下排桩式透空堤的消浪效应。为此，本文基于浙江省某实际防波堤工程，进行了波浪整体物理模型试验，针对桩间不带肋板和带肋板的两种不同结构形式，研究了排桩式透空堤在不同波向不规则波作用下的消浪效应。

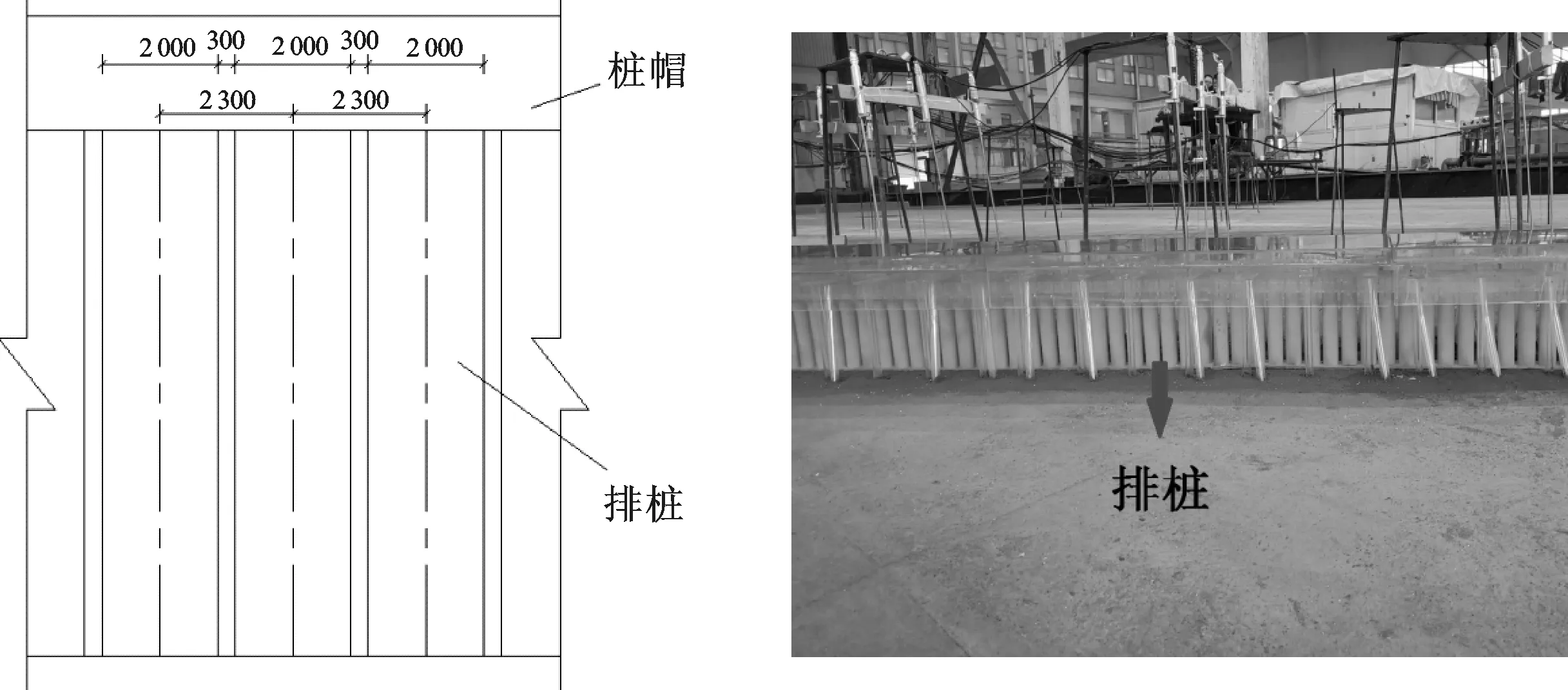
1-a 排桩式透空堤正面示意图1-b 排桩式透空堤物理模型正面图图1 排桩式透空堤正面图(单位：mm)Fig.1 Front view of pile breakwater

1 物理模型设计与试验方法

1.1 模型设计

本模型试验在河海大学江宁校区海岸实验厅的大型波浪港池中进行。港池尺寸为60 m×40 m×1.5 m，池中装有可移动式不规则波造波机系统，能够按照要求模拟规则波和各种谱型的不规则波，同时港池四周装有消浪设施以减小波浪的二次反射。

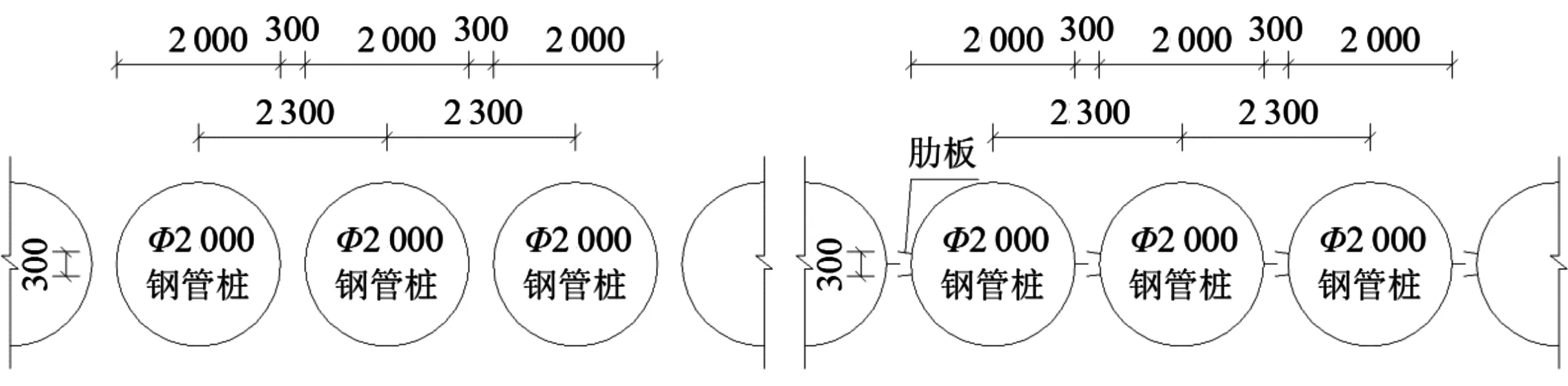
2-a 桩间不带肋板2-b 桩间带肋板图2 两种不同的排桩结构形式(单位：mm)Fig.2 Two different structure forms of piles

排桩式透空堤的物理模型用有机玻璃制作，分为防波堤和引桥两部分。防波堤面板厚3.4 m，桩径为2 m，桩间距离长0.30 m，分为桩间不带肋板和带肋板两种不同结构形式，排桩式透空堤以及桩间肋板的具体形式如图1和图2所示。模型比尺根据试验对象的结构尺度，港池的大小以及最大的波高，综合考虑以上因素后决定采用1∶60的试验比尺。根据试验要求，堤后沿着堤身方向分4处布置浪高仪，每处布置3根浪高仪(第一根浪高仪距离堤后0.1 m，之后每两根间隔1 m)用以测量堤后波高。波高采用DJ-800型多功能数据测量系统进行采集，每处3根浪高仪处理的数据最终取平均值作为该处波高的代表值(即#1-1，#1-2，#1-3三处浪高仪波高数据取平均值最终作为该处波高的代表值#1)，模型平面布置及浪高仪的摆放位置如图3所示。

1.2 试验方法

此次试验根据要求采用不规则波进行，不规则波频谱为JONSWAP谱，谱峰升高因子γ= 3.3，波要素的率定均满足《波浪模型试验规程》(JTJ /T234-2001)的相关要求[17]。试验波向分为左侧来浪，前方来浪和右侧来浪三个方向，入射角以波浪正向垂直作用于防波堤为0，则三个入射方向的波浪入射角分别为58°、10°、55°，如图3-a所示。影响防波堤透浪系数的因素很多，在本次试验中，主要考虑相对入射波高Hs/△h、相对波长L/d、相对堤宽B/L、不同波向和桩间肋板对排桩式透空堤消浪能力的影响，关于试验的波浪要素详见表1。本次试验每个组次进行三次取平均值以避免偶然因素造成的误差，保证试验的准确性。排桩式透空堤的断面形式及上述各物理参数的定义如图4所示。

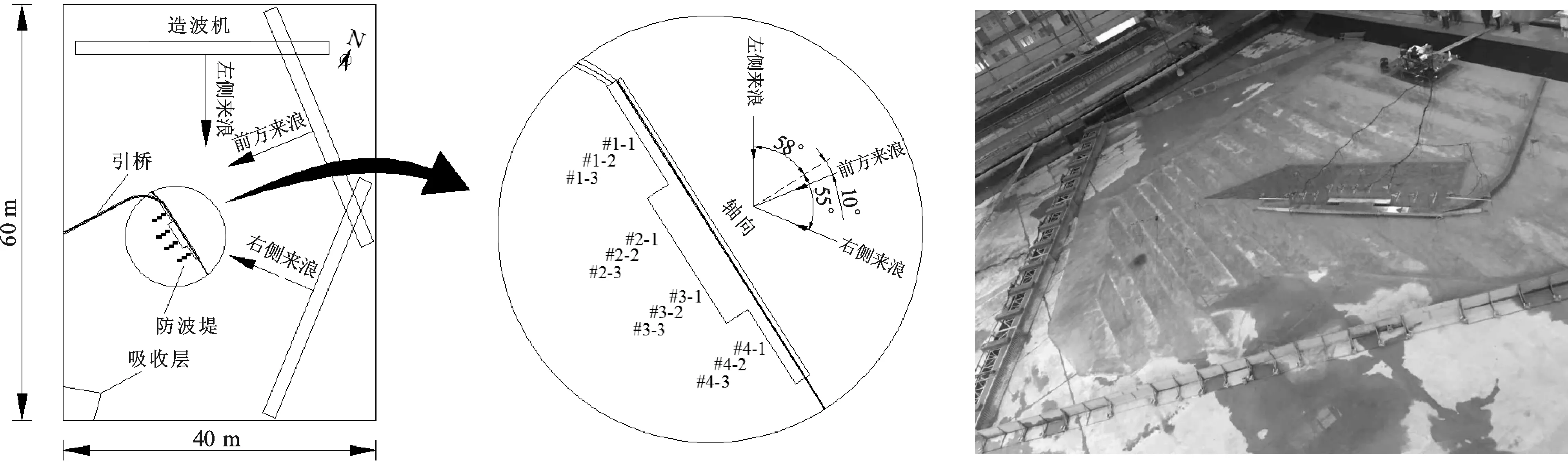
3-a 物理模型试验布置示意图 3-b 物理模型试验场地布置图图3 物理模型试验平面布置图Fig.3 Overall layout of the model test

表1 试验波要素Tab.1 Wave design elements

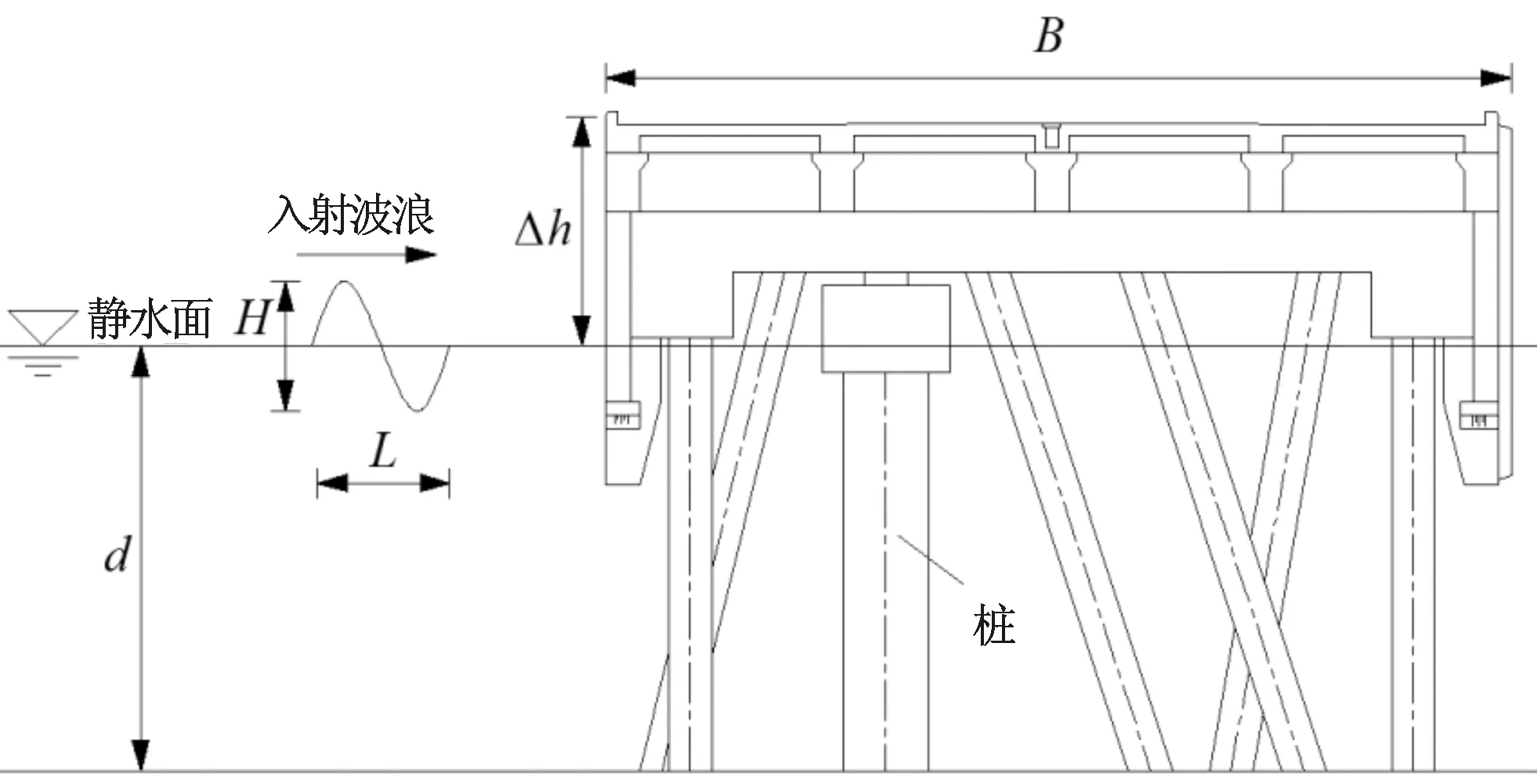
图4 排桩式透空堤断面形式及各物理参数示意图Fig.4 Sketch of the permeable breakwater section and definitions of the physical parameters

2 透浪系数影响因素分析

透浪系数Kt是防波堤最为关键的参数指标，其物理含义系堤后透射波高与堤前入射波高之比，反映了防波堤的消浪能力[18]。

2.1 相对入射波高的影响

图5是前方来浪作用下(入射角为10°)桩间不带肋板透空堤各测量位置下的Kt随相对入射波高Hs/△h变化而变化的情况。由图所见，透空堤堤后各测量位置的Kt均随相对入射波高的增大先减小后增大。造成这种情况的原因是：(1)当相对入射波高逐渐增大但仍小于1.0时，更多的水体会与透空堤的桩体相互作用，从而产生更大的波能损耗，使堤后波能总量减小得更为明显，波高值更小；(2)当相对入射波高继续增大到大于1.0时，波浪的波峰面高程就会高于透空堤顶面高程，从而会产生越浪，一部分水体不通过与透空堤接触直接越过堤顶面到达堤后，从而使波能损耗减小，对波高的消减作用降低。此外，假如入射波高能够继续增大到可以忽略透空堤作用时，透空堤对波高的衰减作用就会不再明显。

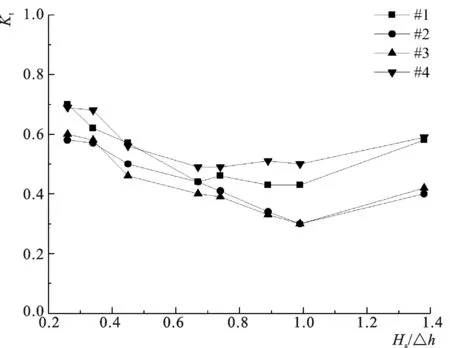
图5 相对入射波高Hs/△h对透浪系数Kt的影响Fig.5 Influence of relative wave height Hs/△h on the wave transmission Kt

2.2 相对波长的影响

图6是前方来浪作用下(入射角为10°)桩间不带肋板透空堤各测量位置下的Kt随相对波长L/d变化而变化的情况。如图所示，随着相对波长的增大，各位置的Kt均呈现增大趋势。当相对波长较小时，Kt增大得更为明显，当相对波长较大时，各位置的Kt均趋于稳定。由此可见，当相对波长越小，波浪与透空堤相互作用后从而产生的水体紊动更为剧烈，消浪效果更为明显。

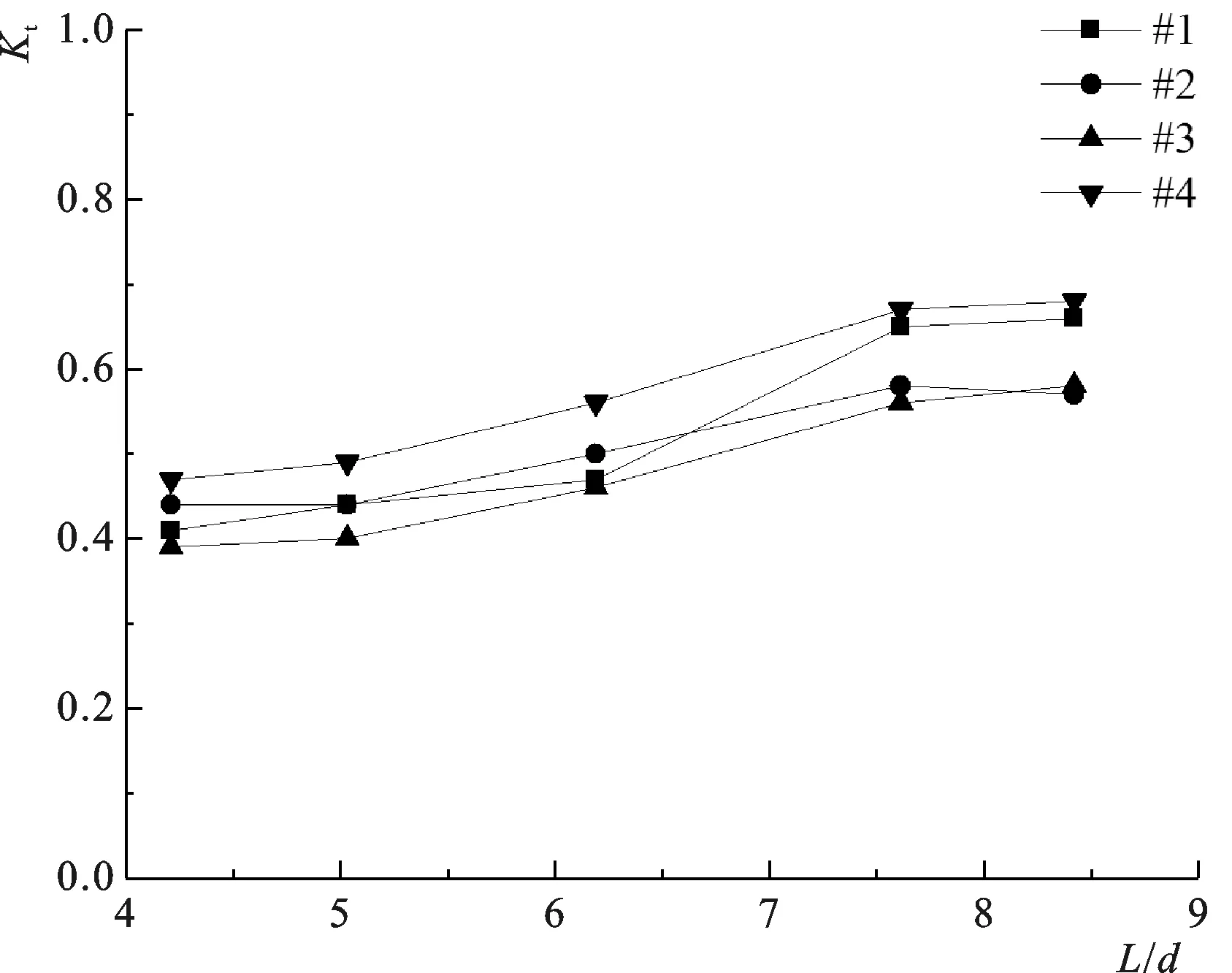
图6 相对波长L/d对透浪系数Kt的影响Fig. 6 Influence of relative wave length L/d on the wave transmission Kt

2.3 相对堤宽的影响

图7是前方来浪作用下(入射角为10°)桩间不带肋板透空堤各测量位置下的Kt随相对堤宽B/L变化而变化的情况。由图可见，随着相对堤宽逐渐增大，各位置的Kt均呈现出减小的趋势。当相对堤宽较小时，Kt的减小趋势较为明显，当相对堤宽B/L大于0.35后，相对堤宽的持续增大对Kt的减小作用就不再明显。这说明堤宽的增大能促进堤后波能的耗散，但不能通过持续的增大来进一步消减堤后波高。另一方面也说明了长波对于堤宽的增大更为敏感，加大堤宽对于长波波高的削减作用大于对于短波波高的削减作用。

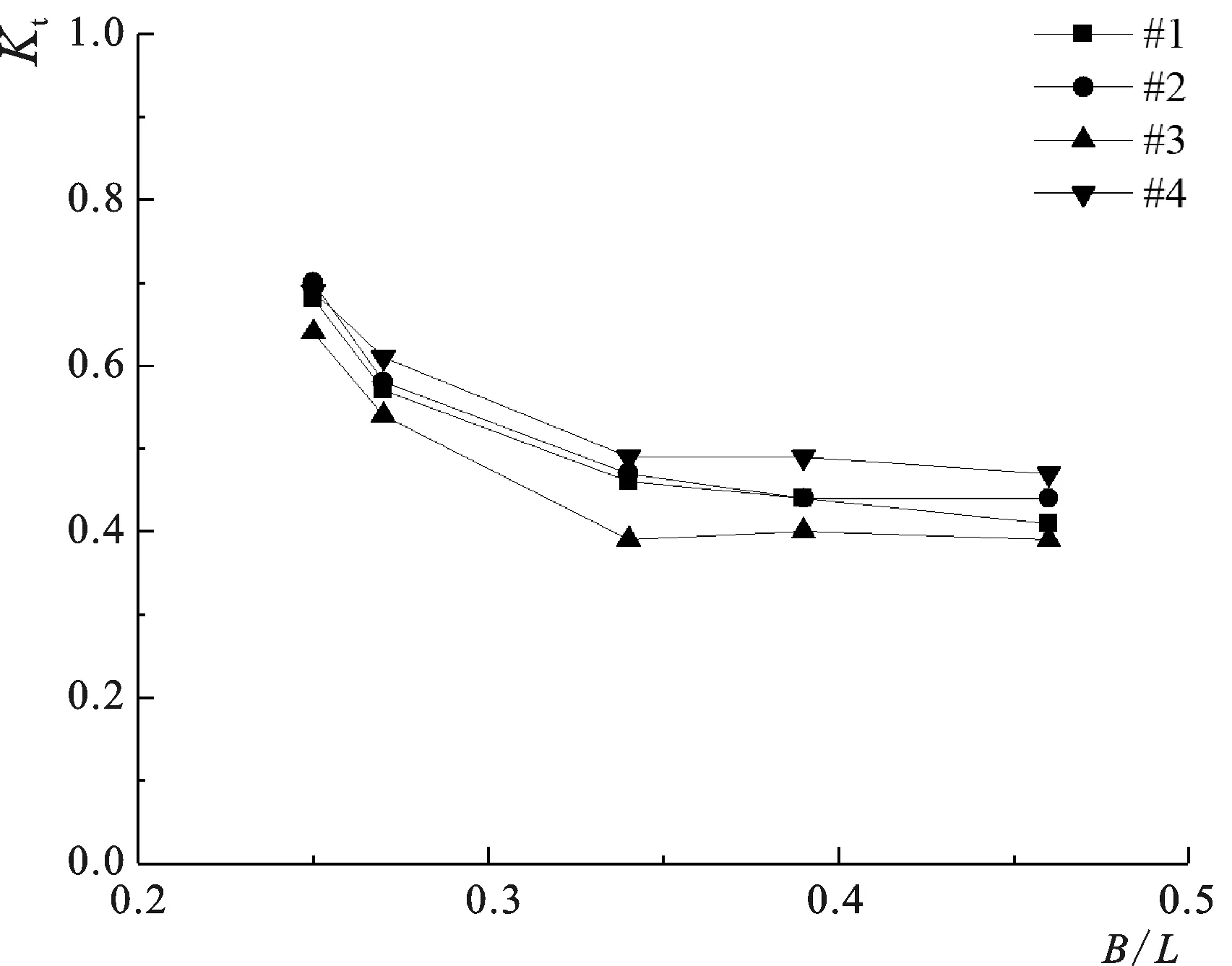
图7 相对堤宽B/L对透浪系数Kt的影响Fig.7 Influence of relative width of breakwater B/L on the wave transmission Kt

2.4 不同波向的影响

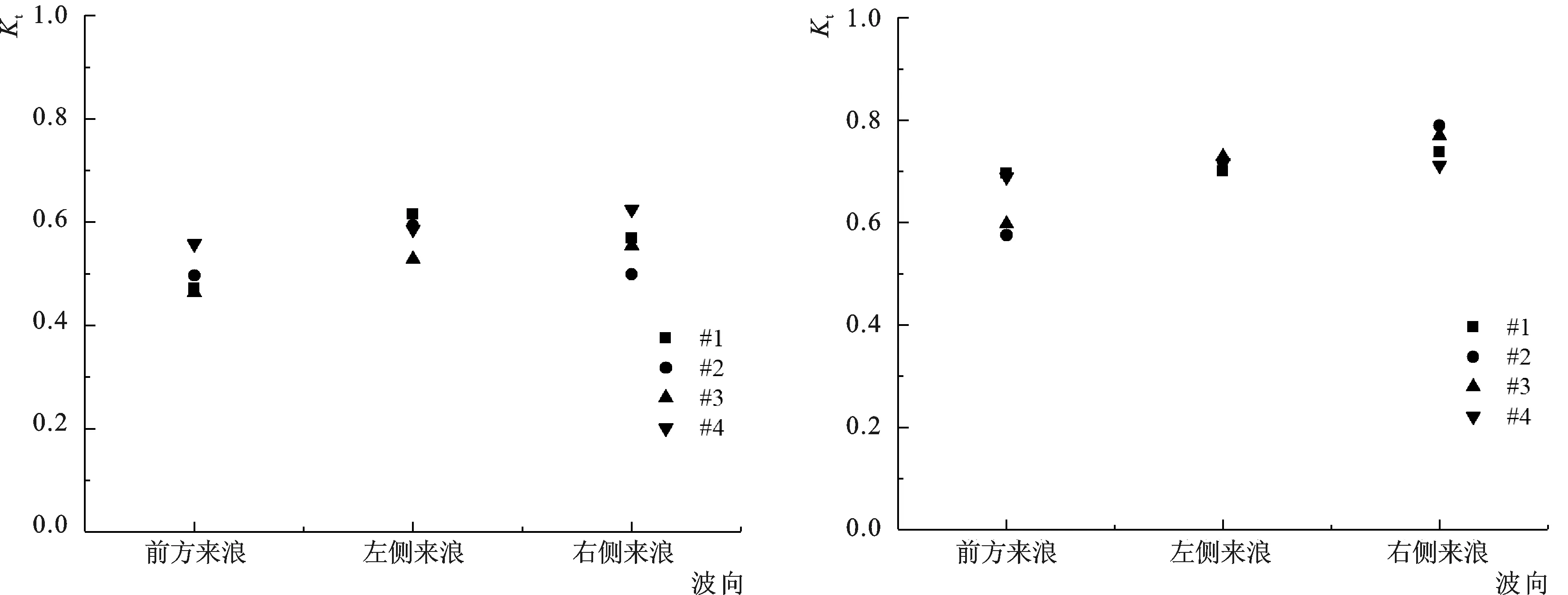
本次研究共进行了左侧来浪、前方来浪和右侧来浪三个方向的不规则波试验，图8分别是d=14.6 cm和d=11.5 cm的各组次下桩间不带肋板透空堤不同测量位置的Kt随不同波向的变化情况。由图可见，相比于前方来浪(入射角为10°)，左侧来浪和右侧来浪(入射角为58°和55°)情况下的Kt在各测量位置均呈现较大的值。造成这种现象的原因是与正向入射相比较，波浪斜向入射一方面会造成透空堤有效掩护长度变短，另一方面会明显增大防波堤堤头的波浪绕射效应，使得堤后水体拥有更大的波能，波浪绕射叠加后的堤后波高更大，Kt也随之增大。

3 桩间肋板对透浪系数的影响

本次研究还进行了桩间带肋板的排桩式透空堤透浪系数试验，表2显示了不同波向下有无肋板对排桩式透空堤透浪系数的对比影响。根据表2所示，带肋板排桩式透空堤的透浪系数明显小于不带肋板的排桩式透空堤，加上肋板后的透空堤具有更为显著的消波能力，桩间肋板对于透浪系数的衰减率在10%～60%之间。此外，该衰减率在水深较小的情况下达到较大值，随着水深的增加，衰减率呈现下降趋势。这是由于水深增加后，堤顶越浪会随之增大，一部分水体不通过排桩间距直接越过堤顶到达堤后，减小了桩间肋板的阻挡作用，导致对堤后波高的削减效应降低。

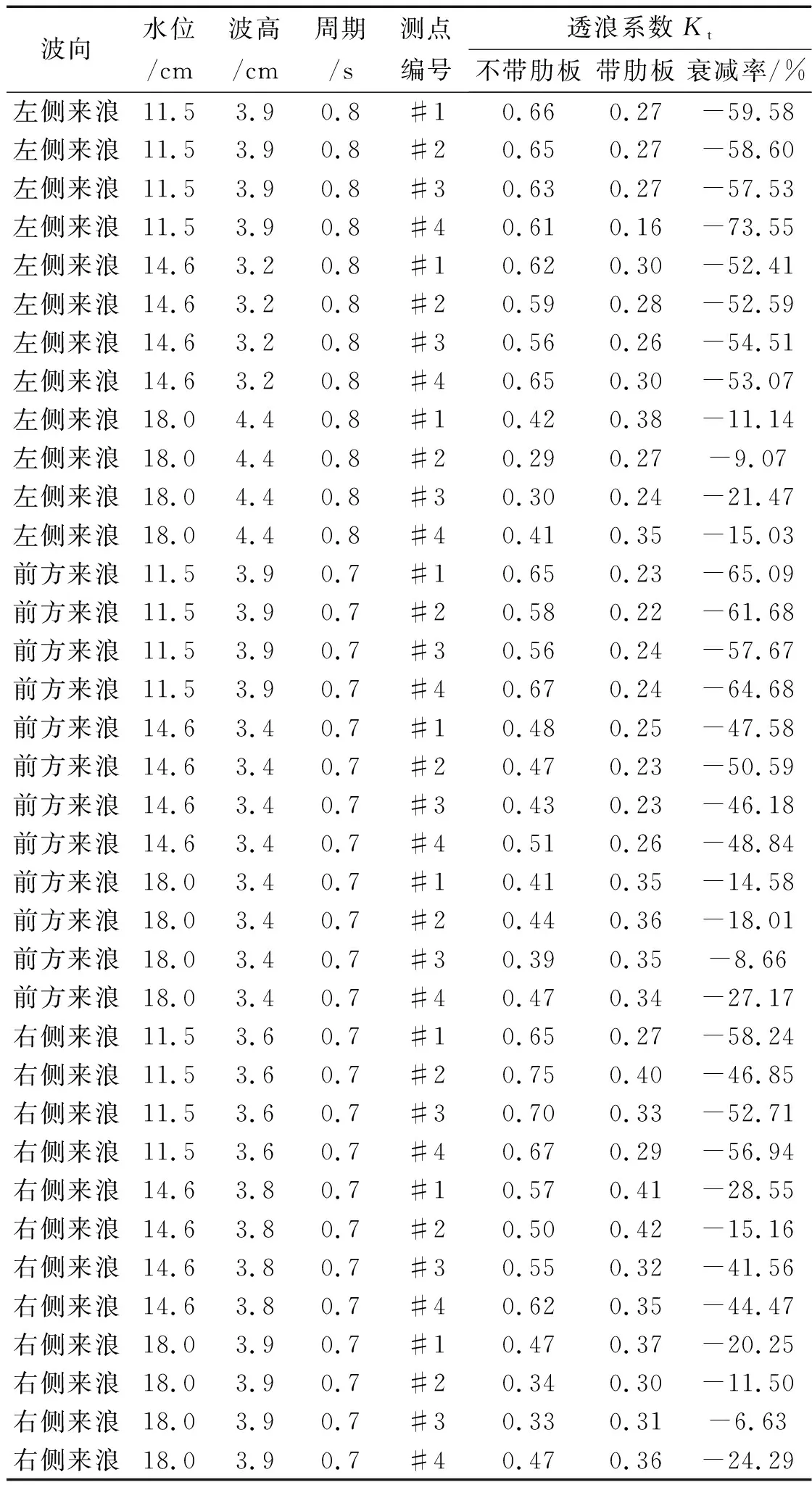
表2 不同波向下有无肋板对排桩式透空堤透浪系数的影响Tab.2 The influence of ribbed plate on the wave transmission coefficient of pile breakwater under different wave directions

4 堤后波高试验值比较

本次试验测得了整体波浪物理模型试验下的堤后波高，与此同时交通运输部天津水运工程科学研究所也进行了相对应的断面物理模型试验[19]和整体数值模拟计算[20]。不同于整体物理模型试验可以同时考虑波浪的透射、绕射和越浪效应，断面物理模型试验只能主要反映波浪的透射效应以及整体数值模拟计算只能主要反映波浪的绕射效应。

表3、表4和表5分别是左侧来浪、前方来浪和右侧来浪波向下各测量位置的堤后波高整体物理模型值、整体数值模拟值和断面物理模型值。根据各表所示，断面物理模型值、数值模拟值和整体物理模型值总体上相差不大，但是仍有部分断面物理模型值和数值模拟值小于整体物理模型值，因此仅凭单方面的断面物理模型值或数值模拟值对于防波堤的结构设计是偏于危险的，存在一定的安全隐患。

表3 左侧来浪作用下堤后波高试验值比较Tab.3 The comparison of wave height value in each berth under irregular waves with left direction

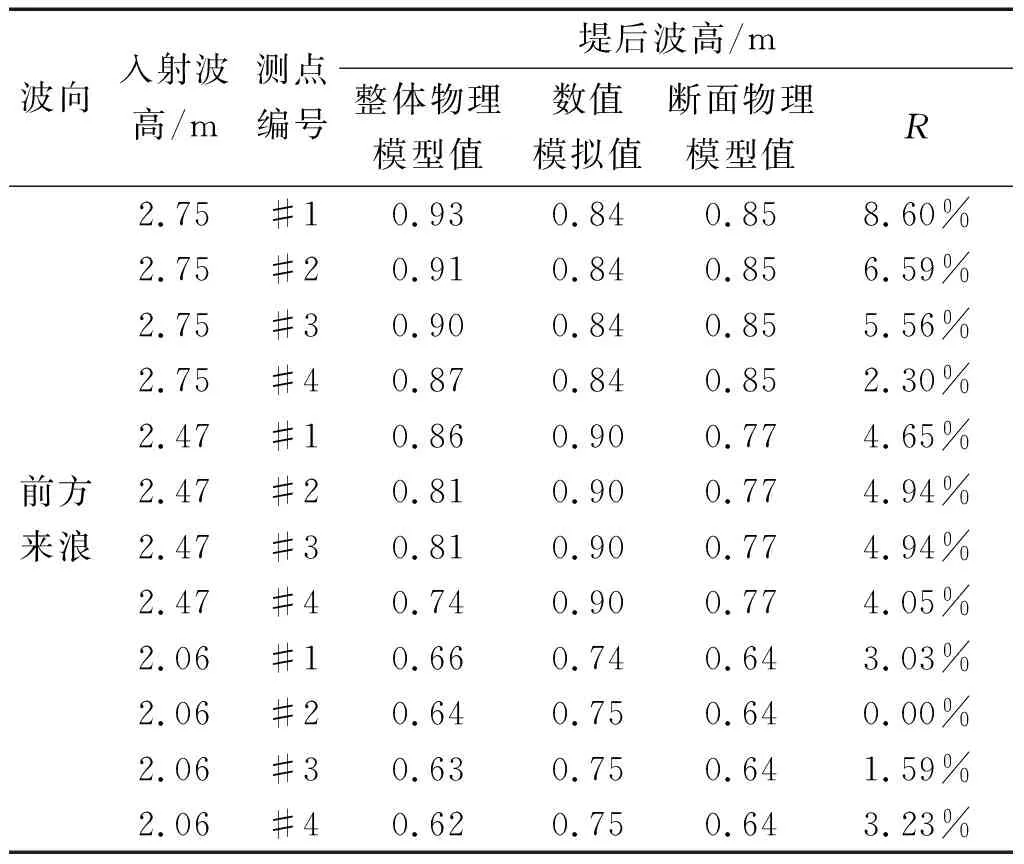
表4 前方来浪作用下堤后波高试验值比较Tab.4 The comparison of wave height value in each berth under irregular waves with front direction

为了更好地评价整体数值模拟值和断面物理模型值与整体物理模型值之间的误差，表3、表4和表5给出了整体数值模拟值和断面物理模型值与整体物理模型值的误差百分比，误差取值如下式所示

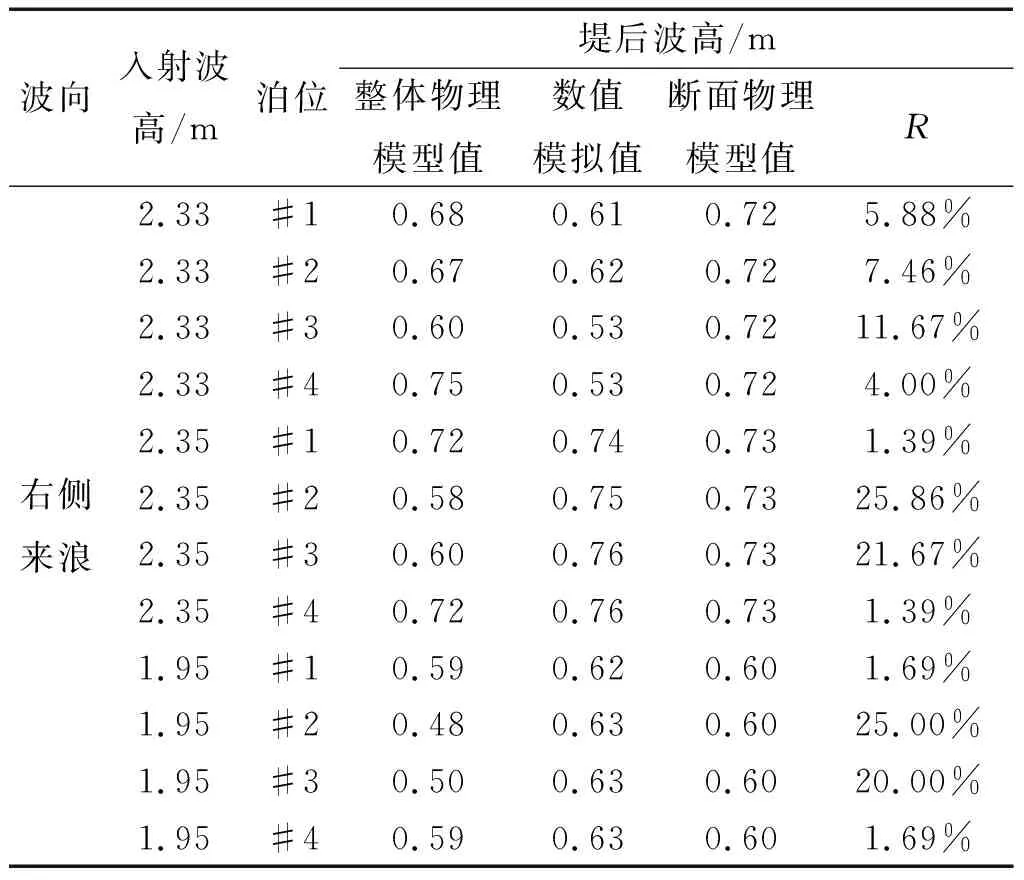
表5 右侧来浪作用下堤后波高试验值比较Tab.5 The comparison of wave height value in each berth under irregular waves with right direction

(1)

式中：R为误差百分比；H断面为断面物理模型波高值；H整体物模为整体物理模型波高值；H整体数模为整体数值模拟波高值。

根据各表所示，由上述公式(1)计算所得的误差百分比最大可以达到40%，其中左侧来浪和右侧来浪波向下的误差平均值分别为18.74%和10.64%，而正向来浪作用下的误差平均值仅为4.12%。因此，当排桩式防波堤主要受正向来浪作用时，整体物理模型值与整体数值模拟值和断面物理模型值的误差较小，在实验条件受限情况下，可以仅根据断面试验和数值模拟计算进行初步的结构设计。然而，当排桩式防波堤受斜向来浪作用较为明显时，数值模型值和断面物理模型值与整体物理模型值之间存在不可忽视的误差，此时应该配套进行整体物理模型试验来进一步确定结构设计参数。

5 结论

本次试验在不同波向的不规则波作用下，探讨了排桩式透空堤透浪系数的变化规律，其主要结论如下：(1)从入射波要素进行分析，桩间不带肋板透空堤的透浪系数Kt随着相对波高的增大会呈现出先减后增的现象；而对于相对波长的增大，Kt则表现出在一定范围内显著地增加。从透空堤结构形式进行分析，相对堤宽的加大能引起Kt增加的趋势；(2)在不同波向作用下，由于波浪斜向入射时透空堤的有效掩护长度变短以及堤头的波浪绕射效应增大，导致叠加后的堤后波高变大，从而左右侧来浪的透浪系数Kt较大于前方来浪的透浪系数；(3)与不带肋板的排桩式透空堤相比，桩间加上肋板后明显增强了排桩式透空堤的消浪能力，对于透浪系数的衰减率在10%～60%之间；(4)当排桩式防波堤主要受正向来浪作用时，整体物理模型值与整体数值模拟值和断面物理模型值的误差较小，在实验条件受限情况下，可以仅根据断面试验和数值模拟计算进行初步的结构设计。然而，当排桩式防波堤受斜向来浪作用较为明显时，数值模型值和断面物理模型值与整体物理模型值之间存在不可忽视的误差，此时应该配套进行整体物理模型试验来进一步确定结构设计参数。