大学生就业当中的数学原理及其应用

卢 鹏，王 璐，徐昌贵，张兴元

(西南交通大学数学学院，四川成都 610031)

每一个大学生在毕业时都面临着就业选择这一问题，但大多数学生都觉得就业非常的困难，究其原因网络上有这样一个观点就是大学扩招，我国从1999 年开始进行大学扩大招生，每年招收大学生的数量逐步增加，近两年达到峰值[1].2019 年，全国高校毕业生人数约830 万[2]，求职现场异常火爆.但是这种观点是片面的，随着我国经济的快速增长，各行各业需要的岗位数量也是相当多的，国家发展与改革委员会主任何立峰曾说：经济每增长一个百分点，可创造新增就业岗位170 万左右.而近5 年来我国经济平均增长率[3]约为7%，每年足以提供上千万新增岗位，所以并不是因为工作数量不够，而是大学生在择业时的不确定性和多变性，可以从以下两点进行说明：①价值观——很多大学生找工作时最关注就是年薪多少，工作所在地是否是大城市等等；②招聘制度——现有招聘方式是单位分批来校招人，很多大学生还没等到最满意的单位来就已签约；久而久之我们的大学生就觉得就业非常的困难.

本文并不从定性方面考虑大学生的就业问题[4-9]，而是针对现有招聘制度，运用数学中概率论[10]的知识对大学生如何选择工作这一过程进行数学建模[11-13]，得到大学生的最优选择策略，并对结果进了验证、应用与改进.

1 问题分析

1.1 问题假设

(1)假设大学生参与若干个单位招聘，其中有部分单位以不同的先后顺序向该学生提供就业协议.假定对提供就业协议单位按满意度从小到大进行编号：1，2，…，N，即编号为N的单位最满意. 每个学生根据自身条件，并结合以往经历和经验确定自己的N值.

(2)面对提供就业协议的单位，大学生只能做出接受和拒绝两种选择，已经被拒绝的单位不会再次招聘这位大学生.

1.2 具体分析

基于上述假设，想要找到这样一种策略，使得大学生以最大的可能在第一次选择接受的那个单位就是N.最简单的一种策略：一旦有单位向该学生提供就业协议，学生就选择接受.在此策略下以1/N的概率找到自己的N，显然不是一种好的策略.我们提出这样一种策略：对于先提供的M个单位，无论学生感觉如何都选择拒绝；从第M+1 个单位开始，只要这个单位的比前面M个单位都好，那么选择接受，否则选择拒绝.

特殊情况：以N= 3 为例说明：三个单位招聘大学生，共有六种排列方式：

123，132，213，231，312，321

如果学生采用上述最简单的策略，那么只有最后两种排列方式选择到“3”，概率为2/3! =1/3.采用刚刚提出的策略，并取M=1.基于这种策略，“132”、“213”、“231”这三种顺序下学生都会在第一次做出选择接受时遇到“3”，这样就把概率增大到3/3! =1/2.

1.3 明确的数学问题

对于一般的N，什么样的M才会使大学生选到最满意单位的概率达到最大值?

2 模型的建立与求解

2.1 模型建立

1 到N个数字排列共有N!种可能.当在第i位置(M ＜i≤N)学生第一次选择接受时遇到的就是最满意单位(编号为N)，排列需要满足下面两个条件：

①N在第i位置：概率为1/N；

②从1 到i-1 个位置中的最大数字必须落在前面M个位置，概率为M/(i-1) ；

数学模型为：

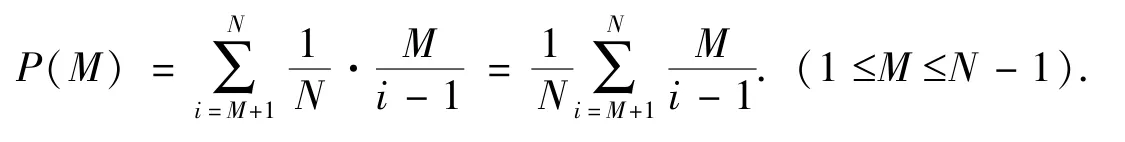
2.2 模型求解

2.2.1 离散方式求解

先用数学软件对模型进行简单分析，利用N与M之间的关系画出图1，从图中可以发现最优解出现在N的中部，而且规律先增后减，单峰模式.

图1 不同N 值下最优解M 出现的位置Fig.1 The location of the optimal solution M under different N values

为了简化方程组的计算，可等价为：M= min{M≥1：P(M)＞P(M+1)} ，

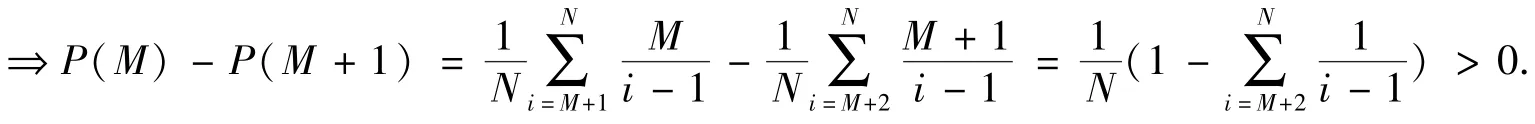
又由于当x ＞0 时， 有 ln(1+x)＜x，则

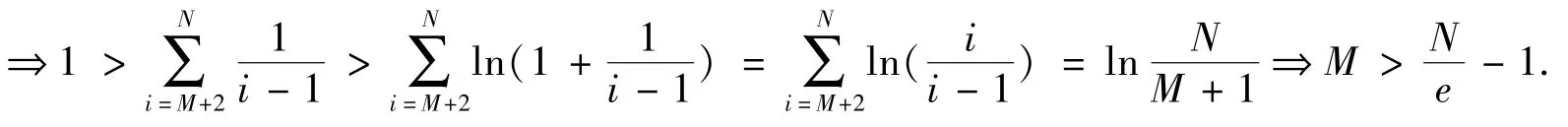
结果：当M取[N/e]时，该表达式取得最大值.

2.2.2 连续方式求解

令x等于M/N的值，并假设N充分大，这样就把离散模型连续化，其几何意义代表图2 中的阴影面积，则上述概率公式可以近似表示为积分形式：

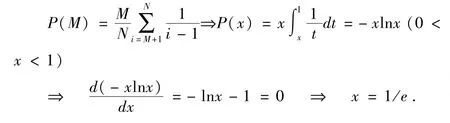
结果：1/e大约等于37%，即M/N= 37%

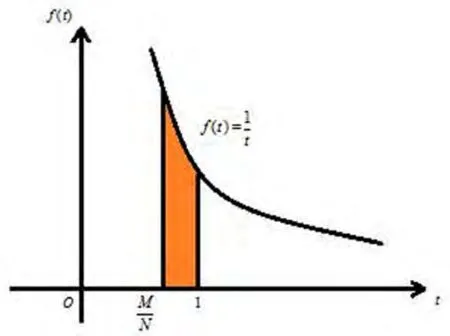
图2 离散求和积分形式Fig.2 Discrete summation integral form

2.3 结果说明

经过对比可以发现，离散方式与连续方式求解结果相同.由此可得如下策略：如果招聘单位共有20 个，估计自己的N为10，则拒绝前3 个(37%原则，另外拒绝前四个最大概率稍小于拒绝前3 个)的招聘单位，从第4 个招聘单位开始选择，如果比前面更满意则接受，否则拒绝.其中出现了三个37%准则.

第一：前面37%的单位不选；

第二：选到最满意单位的概率为37%(需把最优解带回模型算出最大概率)；

第三：一个单位都选不到的概率为37%.

2.4 结果检验

运用计算机仿真[14-15]来检验模型的正确性，取N= 20 ，则产生1 到20 随机排列的整数数列，再取M为不同的值，利用提出的策略，模拟整个招聘过程，结果如表1 所示：

表1 取N=20，重复1000000 次，计算时间约130 秒Table 1 Take N = 20 and repeat 1000000 times. The calculation time is about 130 seconds.

图3 P(M)与M 的直方图Fig.3 Histograms of P(M) and M

根据表1 中的数据，画出P与M的直方图，由图3 所示，图3 中左边图形为模型计算结果，右边图形为仿真计算结果，从表格中可以看出最大绝对误差为0.0006，非常的小.从图形中也基本看不出两副图形之间的差别，所以结果是相当可靠的.

2.5 模型应用

2.5.1 钻石问题(著名微软面试题)

一到十楼每层电梯口都放着一颗大小不一的钻石.你乘电梯从一到十楼，每层电梯门会开一次，并且你只能拿一次钻石.请问你如何能拿到最大的一颗?

实施方案：电梯前三层不选，从第四层开始比较，如果比前面的都大就选择，否则继续下一层.这样能选到最大钻石的概率为40%左右.

2.5.2 旅游景点物品购买策略

随着生活水平的不断提高，出国旅游的人们是越来越多，大家来到一个陌生的地方(亚洲、非洲、欧洲)，想买些纪念品给国内的好友，如何进行购买呢?

策略方案：先不要着急在第一时间购买，而是先逛过去，了解一个大概的价钱，在差不多走过街道三分之一的时候才开始(比较)购买， 这样最不容易被讹到.

2.5.3 相亲节目中女嘉宾的最优选择

现在我国相亲节目众多，比较有影响力的有中国式相亲、新相亲时代、非诚勿扰，如果非诚勿扰的女嘉宾想让我们给她一种选男嘉宾的策略，你会如何给她建议?

策略方案：如果女嘉宾打算上10 期节目，估计自己的N为20，则拒绝前7 个(37%)的追求者，从第8 个追求者开始选择，如果比前面更适合则接受，否则拒绝.

3 模型的改进

由前面结果可知，虽然有37%的概率选到最满意单位，但是也有37%的概率一个都选不到.为了降低选不到单位的概率，提出一种方案：降低对解的要求(如：次优解也能接受).

当在第i位置第一次选择接受时遇到的就是最满意(编号为N)或次满意单位(编号为N-1 )，排列需要满足：

①N或N-1 在第i位置；

② 从1 到i-1 个位置中的最大数字必须落在前面M个位置；

③ 若选到N-1 ，还需满足N落在i后面.

3.1 改进的数学模型

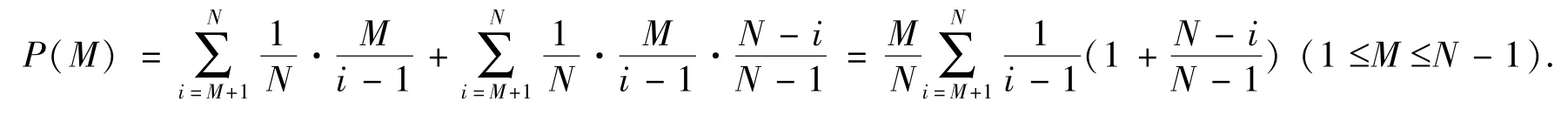
3.2 模型求解与结果说明

要直接理论解出这个数学模型比较困难，但利用Matlab 软件可以很轻松的给出结果，如表2 所示.

表2 模型结果与原模型结果Table 2 Model results and original model results

结果说明(比较原方案)：

① 前30%不选，选中概率约为51.3%(增加1%)；

②空手而归的概率约为30%(降低7%)；

③选中最满意单位概率降低约0.6%；

④选中次满意单位概率增加约1.6% .

从结果可以看出此模型降低了风险，但最优概率降低却不大，是一个好的改进方法.

3.3 模型验证

使用Matlab 进行仿真检验，其中N= 50 ，重复1000000 次，计算时间约660 秒.

图4 模型结果与仿真结果对比图Fig.4 Comparisons between model results and simulation results

图5 两种方法计算结果残差图Fig.5 Residual diagrams of the calculated results of two methods

从图4 中可以看出模型结果与仿真结果几乎一样，从图5 中也可以看出两种方法之间的最大残差为0.001，结合两者说明了模型的正确性.

3.4 更一般的数学模型

为了进一步减少空手而归的概率，我们继续改进模型，共N人，前M个单位不选，对于排名靠前的K个单位都可以接受的数学模型为

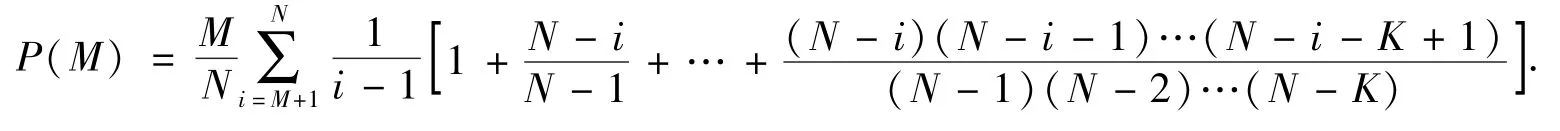
3.5 结果说明

表3 N 取100 时，不同K 值下的各项概率Table 3 N =100 Various probabilities under different K values

根据表中数据我们画出了总的选中概率、最满意单位选中概率与满意单位个数之间的关系，如图6 所示，也画出了选不中的概率与满意单位个数之间的关系，如图7 所示.

从结果可以看出，随着K值的增加空手而归的概率逐步减少，例如当K为10 时，一个都选不到的概率约为15%；最优概率随着K值的增加而逐步减小，减小趋势越来越慢；而选中的总概率随着K值的增加而逐步增大，但增长趋势也越来越缓慢.所以在实际应用当中也不能够把K取得过于偏大.

图6 总概率、最优概率与K 之间的关系Fig.6 The relationship between total probability， optimal probability and K

图7 空手而归的概率与K 之间的关系Fig.7 The relationship between the probability of returning empty-handed and K

3.6 问题拓展

假设用人单位是一批一批来，每批来3 个，总共10 批，相同批次的单位可以同时考虑，不同批次的单位有顺序之分，建立该问题的数学模型并得出最佳选择方案.假设被拒绝的公司可能再次招聘这位大学生(原模型被再次招聘的概率为零)，加入此因素建立数学模型得出最佳选择方案.这两个问题留给大家继续研究.

4 结束语

人的一生有许多重要的选择，择业便是其中之一.通过本文的模型和结果为同学们提供了一种择业上的数学方法，希望对同学们今后有所帮助.也希望同学们在找工作时，除了理性选择，实现自身价值外，更应该像老一辈科学家们学习，为了祖国的社会经济发展贡献自己的智慧和力量.