基于交叠组合稀疏双正则项的全变分图像复原

蔡江乾 蔡光程

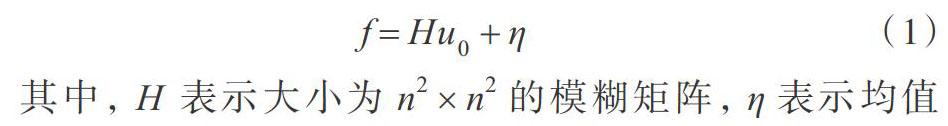
摘 要：为减少图像复原中产生的阶梯效应和边缘模糊现象，引入Hessian矩阵，设计带有交叠组合稀疏化的双正则项。采用一阶交叠组合稀疏的正则项保留边缘，同时采用二阶交叠组合稀疏的正则项缓解一阶正则项产生的阶梯效应;通过构造两个可分离算子最小化问题求解图像复原问题，在乘子交替方向法（ADMM）的框架下，得出求解各子问题的迭代形式，并提出新的复原算法。实验结果表明，峰值信噪比比传统方法至少提高了0.8dB，结构相似度指数最高达0.9，最低为0.72。新算法在去除噪声的同时，有效保留了图像纹理信息。

关键词：图像复原;交叠组合稀疏;全变分;二阶正则项;乘子交替方向法

DOI：10. 11907/rjdk. 201444 开放科学（资源服务）标识码（OSID）：

中图分类号：TP317.4 文献标识码：A 文章编号：1672-7800（2020）007-0204-06

Image Restoration Using Total Variation with Two Overlapping Group Sparsity Regularizers

CAI Jiang-qian，CAI Guang-cheng

（Faculty of Science， Kunming University of Science and Technology， Kunming 650500， China）

Abstract： To reduce the staircase effect and the edge blur in the image restoration， the Hessian matrix is introduced to design two overlapping group sparsity regularizers. The idea is to preserve edges by using the first order term， and remove the staircase effect by using the second order term. Then the image restoration is achieved by constructing the minimization problem of two separable operators. In the framework of the alternating directions method of multipliers（ADMM）， the iterative form of the solution of each subproblem is obtained by deducing the optimization condition， and a new restoration algorithm is proposed. The experimental result demonstrates that the peak signal-to-noise ratio is improved by at least 0.8dB by comparing the traditional method， and the structure similarity index is as high as 0.9 and as low as 0.72. The new algorithm effectively retains the texture information of the image while removing the noise.

Key Words： image restoration; overlapping group sparsity; total variation;second order regularizer; ADMM

0 引言

圖像在形成、传输和存储过程中不可避免地会受到随机噪声的影响，而在医学、天文成像、工业成像等领域中，需要清晰的高质量图像。图像复原的目的是将被噪声污染的图像尽可能地还原为原始图像，其在图像处理中是最经典的线性逆问题之一[1]。本文将原始图像[u0]退化为含噪图像[f]的模型考虑为：

其中，[H]表示大小为[n2×n2]的模糊矩阵，[η]表示均值为0，方差为[σ2]的噪声图像。假设图像大小为[n×n]，与[f]、[u0]和[η]分别是由[n×n]图像矩阵[n]列按顺序叠加成长度为[n2]的列向量。将含噪图像[f]复原回原始图像[u0]，该问题是病态的[2]，为了消除其病态性，Tikhonov等[2]提出正则化方法，通过添加正则项稳定模型的解。正则化方法可将模型（1）转化为以下最小化问题。

其中，[u]表示恢复图像，[？？？2]表示[L2]范数;[φ]称为正则化函数;[λ（λ>0）]是正则项参数，作用是平衡保真项[f-Hu22]和正则项[φ（u）]。Rudin等[3]提出基于全变分（TV）的正则化模型，其中采用各项同性扩散TV模型能够去除噪声，但会使图像边缘部分模糊化;采用各项异性扩散全变分（ATV）模型虽然能够保护图像边缘，但是平坦区域的噪声抑制会不充分，从而导致虚假边缘，产生阶梯效应。

为抑制阶梯效应，更好地保留图像纹理信息， 2015年Liu等[4]提出了一种交叠组合稀疏化的全变分（OGSTV）图像复原模型，该方法充分利用周围像素点梯度信息，突出图像边缘区域和平滑区域的差异性，从而达到更好的复原效果;2018年Ahlad Kumar等[5]提出一种加权交叠组合稀疏的去噪框架，该方法改进了OGSTV模型，更加突出图像边缘区域和平滑区域的差异性;2019年Tarmizi Adam等[6]在OGSTV模型上加入高阶非凸正则化构造模型，其中非凸高阶正则项对图像纹理局部部分有更大的平滑作用，同时可以保留锐利的边缘;还有学者基于交叠组合稀疏化的复原方法进行了相应工作[7-9]。

以上方法均未研究高阶正则项的交叠组合稀疏化。本文设计由Hessian矩阵元素组成的二阶正则项，并对二阶正则项的交叠组合稀疏化进行研究，最后构造出带有交叠组合稀疏化的一阶和二阶双正则项的复原框架，进而弥补一阶正则项单一复原方法。该方法可在去噪和保留图像的纹理信息方面发挥重要作用。

1 OGSTV模型与ADMM

1.1 OGSTV模型

Liu等[4]提出图像[u∈Rn2]的[K×K]点组。

从式（4）可以看出，OGSTV正则项将图像中的某一像素点和邻近像素点的交叠组合稀疏特性结合起来，与传统TV模型（[K=1]）相比，利用相邻像素间相关性可以更加有效地防止图像阶梯效应的出现。

1.2 ADMM

ADMM是求解最小化问题的一种分裂收缩算法，两个可分离算子的线性约束最小化问题[10]为：

其中，[θi：Zi→R]是闭凸函数，[Ai∈Rl×n2]是线性变换， [Zi∈Rn2]是非空闭凸集，[d∈Rl]是长度为[l]的列向量。

引入拉格朗日乘数[μ∈Rl]，则最小化问题（5）的拉格朗日函数为：

其中，[μT] 为[μ]的转置，最小化问题（5）的增广拉格朗日函数是由式（6）与等式线性约束的二次函数  [β2A1z1+A2z2-d22]构成，则

其中，[β>0]为等式约束的参数。

采用ADMM求解最小化问题式（5），其算法形式为：

算法1. 求解最小化问题（5）的ADMM

ADMM充分利用目标函数分离结构[θ1（z1）+][θ2（z2）]，它是增广拉格朗日乘子法（ALM）的一个分裂版本，ALM在每次迭代中以高斯—赛德尔迭代法分解为3个子问题。

2 交叠组合稀疏双正则项全变分模型与算法实现

2.1 交叠组合稀疏双正则项全变分模型

本文设计了带有OGS的双正则项，提出最小化无约束问题。

其中，[λ1，λ2>0]是平衡保真项、一阶正则项和二阶正则项的正则项参数。[Du=（D（1）u，D（2）u）]，其中[D（1）u]和 [D（2）u]由[u]的Hessian矩阵的元素构成，定义为[D（1）u=uxx-uyy]，[D（2）u=-2uxy]，其离散形式分别为;

其中，[D（1）]和[D（2）]表示二阶有限差分矩阵，其大小为[n2×n2]。

通过引入辅助变量[v1，v2，v3，v4，z]，将最小化问题（8）转化为等价的约束最小化问题。

其中，[v]代表[v1，v2，v3，v4];集合[C=[0，255]]，[IC？]为[C]的示性函数，用以恢复0～255之间图像的像素值，集合[C]的示性函数定义为：

因此，约束最小化问题（10）满足式（5）中的框架，可写成：

其中，[E]表示大小为[n2×n2]的单位矩阵，[0]表示长度为[n2]的列向量。

2.2 算法实现

令[H=E]，根據算法1，可以得到如下各子问题。

2.2.1 [u]-子问题

子问题（16）是一个最小二乘问题，可通过求以下正规方程解决。

式（18）的等式两边分别进行傅里叶变换[？]，故：

其中，[？-1]为傅里叶逆变换。如果采用循环边界条件， [？T？=（？（1））T？（1）+（？（2））T？2]是块循环—循环块（BCCB， block-circular with circular-block）矩阵，可以通过快速傅里叶变换对BCCB矩阵进行求解[11]。

2.2.2 [v1，v2，v3，v4]-子问题

[v1]-子问题是交叠组合稀疏化问题。

按照OGS正则项定义，当组大小[K=1]时，[？（v1）=v11]。则[v1]-子问题的最优性条件为：

其中，[ω1=？（1）u（k+1）+μ（k）1β]，sign表示符号函数。当组大小[K>1]时，问题（20）可以使用交叠组合稀疏全变分去噪问题的优化—最小化（MM）方法迭代求解[12]。同理，按照上述步骤可以求解[v2，v3，v4]-子问题。

2.2.3 [z]-子问题

对于[z]-子问题

其最优性条件为：

最后，给出拉格朗日乘数[μ（k+1）1，μ（k+1）2，μ（k+1）3]的迭代形式为：

综合以上分析，提出算法2求解最小化问题（8）。

算法2：求解最小化问题（8）的算法。

（1）初始化[u（k），v（k）i，μ（k）i=0（i，j=1，2，？，5），k=0];[λ1，λ2>0];[β>0]

（2）while终止条件不满足，执行3、4、5、6、7步

（3）根据式（18）计算[u（k+1）]

（4）根据式（19）、（21）、（22）、（23）分别计算[v（k+1）1，v（k+1）2，][v（k+1）3，][v（k+1）4]

（5）根据式（25）计算[z（k+1）=u（k+1）+μ（k）5β]

（6）根据式（26）计算[μ（k+1）1，μ（k+1）2，μ（k+1）3，][μ（k+1）4]，[μ（k+1）5]

（7）[k=k+1]

（8）end while

可以看出，上述算法2是ADMM的一个实例，通过求解各子问题，式（8）的最小化问题即可得以解决。

3 数值实验

为了验证本文算法优良性能，下文展现了一些实验结果。图1为用于实验的6张测试图像，大小为256×256的图像有（a）、（b）和（c），大小为512×512的图像有（d）、（e）和（f）。所有实验都是在配置为Intel（R） Core（TM）i5-4210M CPU（2.60GHz，2.60GHz）和RAM为8GB的64位Windows10的Matlab 2016a桌面上进行。

通過峰值信噪比（PSNR）、均方误差（MSE）和结构相似度指数（SSIM）指标衡量各算法性能。

其中，[u0]和[u]分别表示原始图像和恢复图像，M×N为图像大小。PSNR越高与MSE越低，说明图像复原效果越好。SSIM由Wang等[13]提出，它可以衡量两幅图像相似性。

[μu]和[μu0]分别为[u]和[u0]的均值，[σu]和[σu0]分别为[u]和[u0]的方差，[σuu0]是[u]和[u0]的协方差。[C1=（k1L）2]，[C2=（k2L）2]是用来维持稳定的常数，[L]为像素值的取值范围，[k1=0.01]，[k2=0.03]。SSIM的范围是从0～1，当[u=u0]时，SSIM=1。

本文算法的停止条件满足式（30）。

其中，[u（k）]和[u（k+1）]分别表示第[k]次和第[k+1]次迭代的恢复图像。

3.1 参数设置

首先，需设置参数[λ1]，该参数起到控制一阶正则项的作用。实验中，[λ1]的选择很大程度上决定了图像复原的效果，若只依赖于[λ1]，会导致恢复图像出现阶梯效应及伪影，针对实验中不同程度的含噪图像，因此根据经验设置[λ1∈[0.15，0.95]]。

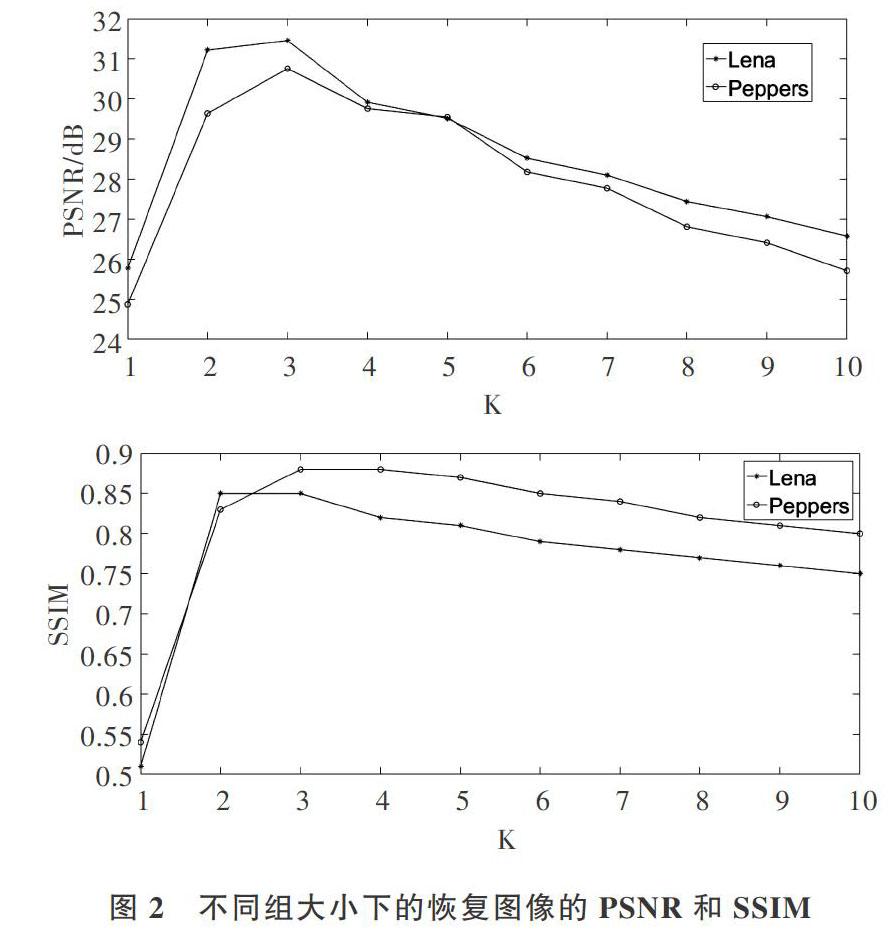
然后，调整重要参数组大小[K]，[K]越大会导致恢复图像过于平滑且会增加CPU的运行时间，为了确定最优的组大小，固定其它参数，通过改变组大小，对加入均值为0、标准差为20的噪声所污染的图像Lena和Peppers进行实验，如图2所示，可以看出[K=3]时，恢复图像的PSNR最大，其恢复图像Peppers的SSIM最大，因此，在实验中设置组大小为3。

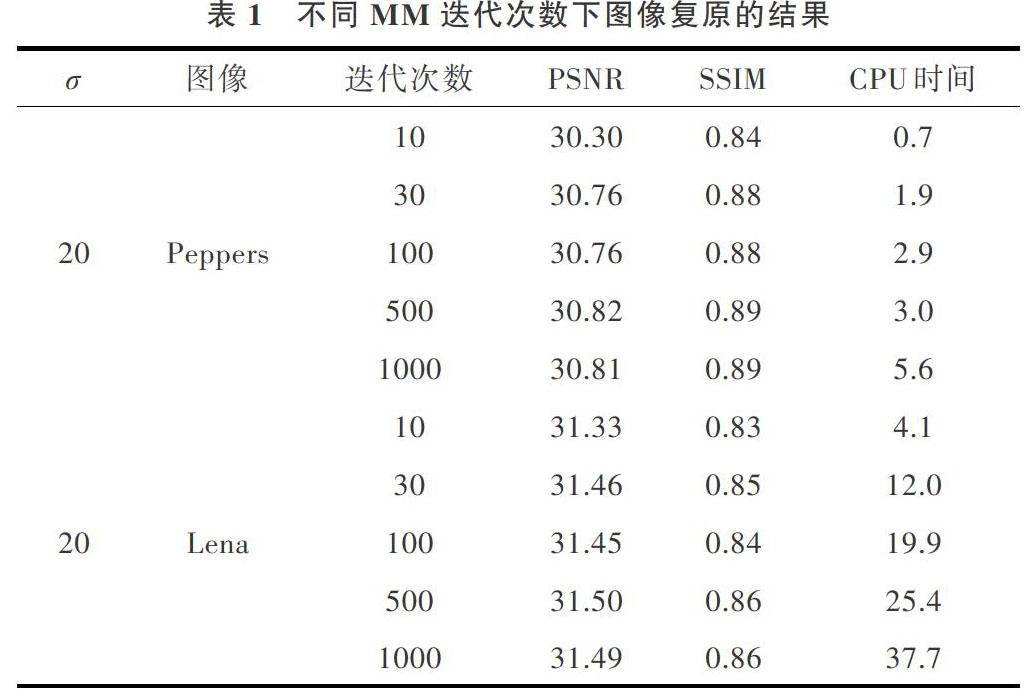
其次，设置OGS子问题（26）所需的MM迭代次数，在表1中，选取含[σ=20]的噪声图像Peppers和Lena进行实验，给出了不同MM迭代次数下图像复原后的PSNR、SSIM及CPU时间。如表1所示，MM迭代次数越大，所消耗的CPU时间越长，但对PSNR和SSIM的影响并不是很大，故此，设置迭代次数为30。

最后，设置二阶正则项的参数[λ2]。通过调整[λ1]值，复原后的图像将产生一定程度的阶梯效应及伪影。另一方面，组越大会使恢复图像越过于平滑。通过调优[λ2]有助于消除恢复图像阶梯效应和伪影，同时保持更清晰的纹理，实验得出[λ2∈[1.5，？？？？6.5]]。在所有实验中，通过人为调参确定给定范围内参数值，从而得到最佳PSNR和SSIM。

3.2 ATV及OGSTV对比实验

将本文方法实验结果与ATV 和OGSTV模型复原效果进行比较，以证明本文方法优越性。在实验中，原始图像被[σ=20]的噪声污染，不同方法复原结果如图3—图4所示。从图中能观察到，本文方法和OGSTV模型均可保护边缘，缓解阶梯效应，特别是对于具有平滑区域的图像，但是OGSTV模型不能充分保留图像纹理和细节信息，而ATV产生了阶梯效应。此外，本文根据得到的PSNR、MSE、SSIM和CPU时间列出6张测试图像实验结果，如表2所示，[σ=20]时，通过不同方法的复原效果各指标比较可以看出，本文方法PSNR、MSE和SSIM均有明显改善，在PSNR方面至少提高了0.8dB，SSIM最高达0.9，最低为0.78，且CPU时间消耗大幅减少。

3.3 BM3D对比实验

基于块匹配与三维滤波（BM3D）去噪方法[14]是图像复原领域公认的主流方法。选取图像Peppers，被[σ=25]的噪声污染，采用本文方法与BM3D方法进行复原，得到PSNR与CPU时间结果，如图5所示，BM3D得出的PSNR高于本文方法得到的PSNR;但是与BM3D相比，本文方法节省了CPU时间，明显降低了时间复杂度。

4 结语

本文提出了基于交叠组合稀疏双正则项的全变分模型，从而构造两个可分离变量的最小化问题;在ADMM框架下，得出了各子问题最优性条件和新的复原算法。实验结果表明，与现有算法（见表2）相比，本文方法得到的PSNR、MSE、SSIM和CPU时间表现更优，且该方法既能较好地缓解阶梯效应，也能有效保留图像纹理信息，视觉效果明显改善。其不足之处是正则项参数和图像组大小[K]需人工设置，不同的含噪图像需经过参数调节才能获得最佳恢复图像。未来工作将致力于设计自适应正则项参数和组大小的选取方法，针对含噪图像的不同区域进行最佳复原，并进一步研究一种加速的复原算法，尽可能降低CPU时间消耗。

参考文献：

[1] VOGEL C R. Computational methods for inverse problems[M].  Philadelphia：  Society for Industrial and Applied Mathematics Press， 2002.

[2] TIKHONOV A N，ARSENIN V I. Solutions of ill-posed problems[M].  Washington： Winston Press，1977.

[3] RUDIN L I， OSHER S， FATEMI E. Nonlinear total variation based noise removal algorithms[J]. Physica D：Nonlinear Phenomena，1992， 60（1-4）： 259-268.

[4] LIU J， HUANG T Z， SELESNICK I W， et al. Image restoration using total variation with overlapping group sparsity[J]. Information Sciences， 2015， 295： 232-246.

[5] KUMAR A，AHMAD M O，SWAMY M N S. An efficient denoising framework using weighted overlapping group sparsity[J]. Information Sciences， 2018， 454： 292-311.

[6] ADAM T， PARAMESRAN R. Image denoising using combined higher order non-convex total variation with overlapping group sparsity[J].  Multidimensional Systems and Signal Processing，2019，30（1）： 503-527.

[7] 范梦佳，周先春. 基于交叠组合稀疏高阶全变分的图像复原[J/OL]. 计算机应用研究. https：//doi.org/10.19734/j.issn.1001- 3695.2019.06.0246.

[8] 马杰，武利涛，张晓严. 一种改进的组稀疏表示图像去噪方法[J]. 微电子学与计算机，2017（6）：99-103.

[9] LIU J，HUANG T Z，LIU G，et al. Total variation with overlapping group sparsity for speckle noise reduction[J]. Neurocomputing， 2016（216）： 502-513.

[10] 何炳生. 我和乘子交替方向法 20 年[J]. 运筹学学报，2018（1）：1.

[11] LV X G， HUANG T Z， XU Z B， et al. Kronecker product approximations for image restoration with whole-sample symmetric boundary conditions[J].  Information Sciences， 2012， 186（1）： 150-163.

[12] SELESNICK I W， CHEN P Y. Total variation denoising with overlapping group sparsity[C]. 2013 IEEE International Conference on Acoustics， Speech and Signal Processing， 2013： 5696-5700.

[13] WANG Z， BOVIK A C， SHEIKH H R， et al. Image quality assessment： from error visibility to structural similarity[J].  IEEE transactions on image processing， 2004， 13（4）： 600-612.

[14] DABOV K，FOI A，KATKOVNIK V，et al. Image denoising by sparse 3-D transform-domain collaborative filtering[J]. IEEE Transactions on image processing， 2007， 16（8）： 2080-2095.

（責任编辑：江 艳）