地震匹配追踪技术与应用研究进展

张繁昌,兰南英,李传辉,印兴耀,吴国忱

(1.中国石油大学(华东)地球科学与技术学院,山东青岛266580;2.中国地质大学(北京)地球物理与信息技术学院,北京100083)

匹配追踪作为一种数据投影分解方法,能够依据非平稳信号自身的特点,将信号在超完备匹配子波库中自适应展开,从而详细研究信号的局部特征。地震信号是一种非平稳信号,利用匹配追踪将其分解成线性无关的匹配子波,对于精细分析地震信号在不同传播时间的局部特征、挖掘地震信号所蕴含的地球物理信息具有重要意义。匹配追踪算法由MALLAT等[1]提出,开启了信号自适应稀疏分解的先河,该算法基于Gabor匹配子波库。随后,CHAKRABO-RTY等[2]将匹配追踪引入到地震信号分析中,实现了地震信号的自适应分解。然而,Gabor匹配子波波形与地震子波相差较大,不利于地震信号的分解。基于此,LIU等[3-4]先后以Ricker子波和Morlet小波构建超完备匹配子波库,迈出了匹配追踪快速分解的第一步。匹配追踪属于贪婪迭代算法,每次迭代的全局遍历寻优是制约分解效率的关键因素。为解决此问题,LIU等[5]提出了动态最优搜索策略,以瞬时属性作为先验约束,降低了各控制参数的搜索区间;WANG[6]给出了三步法匹配追踪算法,加快了计算效率;陈发宇等[7]建立了以频率为主导的匹配子波搜索方式,减少了迭代寻优的计算量;张繁昌等[8]利用Schmidt方法对匹配子波进行正交变换,降低了超完备匹配子波库的冗余;王珺等[9]、蔡涵鹏等[10]及刘霞等[11]引入不同进化算法,实现了匹配子波的直接选取;张繁昌等[12]提出了双参数匹配追踪,进一步减少了控制参数的扫描;LI等[13]、王聪等[14]以及邓世广等[15]分别并行实现了多匹配子波同时搜索。另外,也有专家学者直接从控制参数的先验信息获取方面入手加以改进。张繁昌等[16-17]将匹配追踪引入复数域,采用阻尼最小二乘法同时获取多个匹配子波的振幅和频率参数;杨午阳等[18]使用最大相关性来估计匹配子波位置和能量参数;印兴耀等[19]以局部频率作为约束来获取匹配子波频率先验约束;刘汉卿等[20]利用连续相位求取稳定的频率先验;张繁昌等[21]根据Ricker子波的特点,提出了基于振幅包络指数拟合的频率参数直接获取方法。

采用上述一系列的算法优化,地震匹配追踪在分解效率上得到了质的飞跃,基本满足了实际地震数据快速分解的需求。在计算效率得以保证的基础上,匹配追踪被广泛应用于地震资料处理解释领域,形成新老技术的更新换代。MALLAT等[1]将匹配追踪和Wigner-Ville分布结合,建立了无交叉项的高精度时频分析方法;WANG[22]提出了基于Morlet匹配子波的匹配追踪Wigner-Ville分布;WANG等[23]将信号在混合匹配子波库中分解,实现了基于混合匹配子波的匹配追踪时频分析技术;张繁昌等[24]利用匹配子波复数谱,创建了分辨率高、能量聚焦性好的时频表示方法;之后李传辉等[25-26]又提出了基于Morlet匹配子波的可变分辨率频谱成像方法以及逆时频表征方法。在得到高精度时频分析方法后,宋维琪等[27]利用匹配追踪叠加重建技术有效实现了薄层砂体预测;陈林等[28]开展了时频属性提取工作,得到了抗噪性好的时频属性;张显文等[29]利用“低频阴影”进行了含气储层的识别;张繁昌等[30]通过分析楔形模型的瞬时谱特征,提出高精度砂岩尖灭线的拾取方法;张世鑫等[31]借助匹配追踪时频分析提取了瞬时能量异常属性,并以此实现了可靠的油气预测;张京思等[32]将匹配追踪方法与频率衰减梯度结合,进行了较为准确的叠后烃类检测;张繁昌等[33]基于匹配追踪算法提出了振幅随频率变化的剖面构建方法,并给出了新的地震信号分频技术;杨亚迪等[34]采用高精度时频分析方法求取流体活动性属性,实现了页岩气甜点的准确识别。在地震信号处理领域,匹配追踪凭借自适应分解与重构的优势,也发挥着重要作用。赵天姿等[35]利用匹配追踪进行了时频滤波,有效压制了地震随机噪声;任浩等[36]在稀疏反演框架下,提出了多道匹配追踪去噪方法;宋炜等[37]分析了面波匹配子波和反射波匹配子波的控制参数后,设计了三参数时频滤波器,达到了无损去除面波的目的;张繁昌等[38]根据Q值与地震子波的传播时间及频率的关系,提出了基于匹配追踪的自适应Q值求取方法,并在此基础上实现了叠前道集吸收补偿和频散校正[39];李海山等[40]依据匹配追踪思想,提出了匹配波形相减法来剥离煤层强反射;朱博华等[41]详细讨论了利用匹配追踪分离强反射层过程中的子波控制参数选取问题;何峰等[42]为解决强反射层匹配子波难以准确估计的问题,提出了井控匹配追踪强反射消除技术;张汛汛等[43]根据叠前道集剩余时差的特点,设计了基于匹配追踪算法的剩余时差校正方法;周东勇等[44]将奇偶分解理论与匹配追踪结合,实现了高精度反射系数反演;刘兰锋等[45]根据匹配追踪可逆的特性,给出了一种时频域提高地震分辨率的方法;张繁昌等[46]分析了子波拉伸产生的机理,提出了基于匹配追踪的子波拉伸校正方法。

为了使业界同仁对匹配追踪算法有更深刻、更全面的认识,本文对目前匹配追踪算法的研究进展进行了梳理,主要包括匹配追踪基本原理、匹配追踪加速策略、匹配追踪技术在地震资料处理和解释领域中的应用现状。

1 匹配追踪分解基本原理

1.1 贪婪匹配追踪算法

匹配追踪方法的核心思想是贪婪迭代,即通过多次匹配寻优,在超完备匹配子波库中搜索与地震信号最匹配的子波,从而实现信号的自适应分解。在N维Hilbert空间内,假设D={gγ(t)}γ∈Γ为此空间内的超完备匹配子波库(称为子波字典),对于任一信号f都可利用子波字典对其进行投影分解:

f=〈f,gγ1〉gγ1+R1f

(1)

其中,〈·,·〉为内积算子,gγ1为字典D中第1次迭代所得的子波,R1f为信号经过子波gγ1投影后的残余。根据能量守恒原理,(1)式满足如下能量关系:

‖f‖2=‖〈f,gγ1〉‖2+‖R1f‖2

(2)

匹配追踪需要多次迭代寻优。设迭代到第n次时,投影残余为Rnf,搜索到匹配子波为gγn,那么Rnf又继续被分解成:

Rnf=〈Rnf,gγn〉gγn+Rn+1f

(3)

同样,(3)式也需要满足:

‖Rnf‖2=‖〈Rnf,gγn〉‖2+‖Rn+1f‖2

(4)

重复上述投影分解过程,直至原始信号的残余能量极小,可忽略不计。设信号经过m次匹配追踪分解,最后信号可表示为:

(5)

式中:an是各匹配子波的振幅。由此可见,经匹配追踪分解后,信号可表示为有限数目的匹配子波的线性组合,即稀疏表示。

1.2 正交匹配追踪

上述匹配追踪方法仅考虑每次迭代的残差能量最小,并未考虑不同迭代次数得到的最佳匹配子波之间的正交性(图1a,两次迭代匹配子波gγ1和gγ2不正交),因此出现“短视寻优”现象。为解决此问题,张繁昌等[8]提出一种正交匹配追踪方法,对所得的所有最佳匹配子波进行正交变换(图1b,匹配子波gγ1和gγ2正交),来消除他们之间的冗余分量。

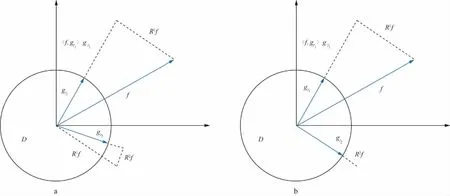
图1 非正交(a)和正交(b)匹配追踪示意

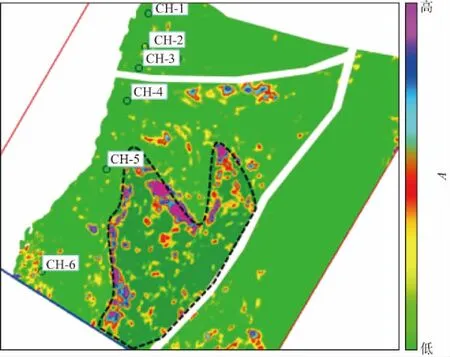
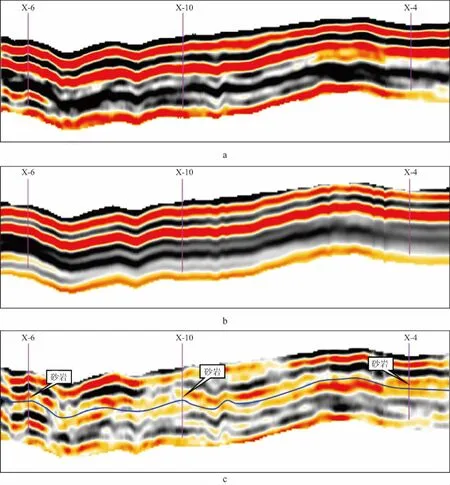
定义gγ所在的空间为V,PVf为f在V上的投影,(up)0≤p

(6)

这样,(up)0≤p

(7)

最终的正交匹配追踪分解方程可描述为:

(8)

1.3 多道匹配追踪

1.1节和1.2节介绍的匹配追踪方法属于单道信号分解方法,在对多道信号分解时,各道匹配子波很容易出现横向不一致的现象。为克服这个问题,充分利用信号的横向相关性特征,WANG[6]提出了“三步法”多道匹配追踪算法。

假设有L道地震信号f=[f1,f2,…,fL],首先计算残差均值道:

(9)

在超完备子波库中,利用残差均值道生成共用匹配子波的初始估计:

(10)

之后,以多通道方式对共用匹配子波进行细化:

(11)

最后,利用共用匹配子波对信号进行逐道分解。

这样,多道信号便可分解为一系列具有相同时移、频率和相位参数,但振幅不同的匹配子波的线性叠加。

2 快速匹配追踪技术

匹配追踪方法虽然可以灵活地实现地震信号的自适应分解,但其在每次迭代寻优时,往往需要信号与超完备子波库中的匹配子波进行巨量的内积运算,因而严重制约了匹配追踪计算效率。如何在保持分解精度的同时,缩小超完备匹配子波库规模,提高计算效率便成为匹配追踪方法的研究热点。近年来,学者们分别从匹配子波母函数类型、匹配子波搜索方式等方面对匹配追踪方法进行了改进和优化,提出了多种快速匹配追踪技术,下面对不同的改进方式进行简要介绍。

2.1 匹配子波母函数

MALLAT等[1]最先利用Gabor函数作为匹配子波母函数,并以此构建超完备匹配子波库,对信号进行自适应分解。Gabor匹配子波如下:

(12)

式中:a为匹配子波振幅;w为高斯函数;μ为时移因子;α为尺度因子;ω为匹配子波频率;φ为匹配子波相位。由于Gabor匹配子波与地震子波在波形上存在较大差异,可以将接近地震子波波形的宽带B样条子波作为匹配子波母函数[47],即:

(13)

式中:q,p分别为频谱上、下限;m为旁瓣参数;fb为相位参数。

由(12)式、(13)式可见,Gabor匹配子波和宽带B样条子波均有5个控制参数,在对信号分解时需要在五维子波库中扫描,以搜索出最佳匹配子波。五维匹配子波扫描计算量庞大,效率极低,无法进行实际应用。因此,LIU等[4]将匹配子波母函数替换为具有4个控制参数的Morlet小波:

(14)

式中:fc为匹配子波频率。随后,具有更少控制参数的Ricker子波也被用来构建匹配子波库[3,18,21,48]:

(15)

这样,匹配子波母函数从Gabor函数进化到Ricker子波,匹配子波库便由五维降到三维,理论上匹配追踪方法计算效率会提高40%。

2.2 匹配子波搜索方式

2.2.1 智能进化算法搜索

为了提高匹配追踪算法的分解效率,全局遍历内积寻优的方式被抛弃,取而代之的策略之一是利用智能进化算法(遗传算法、粒子群算法、模拟退火算法等)进行搜索。王珺等[9]提出了基于遗传算法的快速匹配追踪方法,将直接编码的匹配子波参数作为遗传模型的染色体,信号残差与匹配子波内积值作为适应度函数,每次分解可利用遗传算法进行寻优。刘霞等[11]在粒子群算法中引入一种多项式变异算子,有效避免了搜索的贪婪性。此类方法虽可避免全局遍历寻优,但也受限于智能进化算法效率。

2.2.2 动态最优搜索

动态最优搜索是另一种提高分解效率的策略,即利用先验信息确定匹配子波各控制参数的搜索中心,之后在搜索中心上、下某一区间内进行搜索。在超完备匹配子波库D中,以先验信息点(φ0,u0,ξ0)(图2中蓝点位置)为中心,每个参数各取一定的范围,便构成D的子集D″,D″便是此次迭代的搜索范围,D″={gγ″(t)}γ″∈Γ″,Γ″表示由γ″=(φ″,u″,ξ″)向量组成的集合,α″=[α0-kΔα,α0+kΔα],k为正整数,α表示u、φ和ξ3个参数,Δα表示参数α的采样间隔。

图2 动态最优搜索示意[49]

先验信息点的确定是动态最优搜索方式的核心,直接决定匹配追踪方法的分解精度,下面对匹配子波各参数先验信息点的获取方法进行介绍。

1) 振幅参数。常规匹配追踪分解过程中,每次迭代仅在信号能量最大值处分解一个匹配子波。为提高收敛速度,动态最优搜索方式在寻找匹配子波时,不只局限于能量最大值处,而是在多个能量极点处同时进行搜索,称为多匹配子波分解。对于多匹配子波分解而言,每次迭代的多个匹配子波振幅可采用最小平方法确定[16-17,50]。

2) 相位参数。对于相位参数,一般以分解位置处对应的瞬时相位作为相位搜索中心,在该中心的一个微小区间内搜索,即φ∈[φinst-Δφ,φinst+Δφ],φinst(t)=arctanh(t)/f(t),其中,h(t)为f(t)的正交道,f(t)为原信号。

3) 频率参数。与相位参数一致,匹配子波的频率参数一般也使用瞬时频率作为先验信息。理论上瞬时频率是瞬时相位的导数,但直接由瞬时相位求导得到的瞬时频率会出现没有物理意义的负频率。为求得准确的瞬时频率,提出了多种优化算式,大体分为以下4类。

1) 阻尼最小二乘法[17]。任一复信号s(t)的瞬时频率m(t)可由下式计算:

(16)

写成矩阵形式为:

m=W-1d

(17)

式中:d是所有样点的s(t)h′(t)-s′(t)h(t)构成的向量;W为2π[s2(t)+h2(t)]构成的对角矩阵;m是由m(t)组成的向量。采用阻尼最小二乘法求解该式便得到瞬时频率。

2) 局部频率属性约束法[19]。局部频率属性约束法通过对(17)式施加整形正则化来获得瞬时频率,即:

m=[λ2I+S(W-λ2I)]-1Sd

(18)

式中:λ为尺度因子;S为整形正则化算子。

3) 连续相位求导法[17]。分析发现,利用主值相位求导的瞬时频率之所以出现负频率,其原因在于主值相位存在突变点。连续相位不存在突变点,能够有效解决上述问题。定义连续相位为φ,主值相位为φ,χ,ζ分别为连续算子和缠绕算子,那么连续相位可描述为:

φ(i+1)=χ{ζ[Δφ(i)]}+φ(i)

(19)

求得连续相位后,再对其求导,便可求取稳定的瞬时频率。

4) 振幅包络指数拟合法[21]。此类方法利用Ricker子波振幅包络服从指数分布的特点,在确定匹配子波频率时,只需使用指数函数对信号包络进行拟合,便可直接求取匹配子波频率参数。

2.2.3 并行搜索

多匹配子波分解在每次迭代寻优过程中,匹配子波是在多个能量极点处同时搜索,其搜索过程相互独立,互不干扰。因此,多匹配子波分解具有十分良好的并行化特征。根据这一特点,LI等[13]提出了基于GPU和多核CPU的匹配追踪并行算法。图3给出了基于GPU的匹配追踪并行算法流程。GPU并行匹配追踪算法利用多个GPU同时搜索多个匹配子波并返还至CPU,之后在CPU中利用最小平方法确定各匹配子波振幅参数,由此实现信号的一次迭代并行分解。基于多核CPU的匹配追踪并行算法[49]与基于GPU的匹配追踪并行算法原理基本一致,不同之处在于使用主进程将各极点位置派发到各节点,之后各节点采用动态最优搜索方式进行匹配子波的搜索。并行匹配追踪方法的分解效率显著提升,满足了大规模地震数据快速处理的要求。

图3 基于GPU的匹配追踪并行算法流程[49]

3 地震资料处理解释中的应用现状

匹配追踪可根据地震信号自身的特点,将信号在超完备匹配子波库中自适应分解,从而实现地震信号的稀疏表示。在克服了计算效率低这一缺陷后,匹配追踪技术越来越广泛地应用到了地震资料处理及解释中,如匹配追踪时频分析、薄储层预测、尖灭线识别、强反射剥离、剩余时差校正、吸收补偿、频散校正、提高分辨率等。

3.1 时频分析

时频分析作为一种非平稳信号分析工具,能够有效凸显地震信号在时频域的局部特征,提高地震资料对特殊地质体的解释能力。匹配追踪将地震信号分解成一系列匹配子波的组合,利用这些匹配子波的时频特性能够更有效地表征地震信号的局部特征。

对各匹配子波的Wigner-Ville分布(WVD)求和,可以得到地震信号的时频谱:

(20)

式中:WVD[gγn(t,f)]为匹配子波gγn(t)的Wigner-Ville分布。图4对比了传统子波与匹配子波的WVD。由图4可见,某地震记录(图4a)匹配子波的Wigner-Ville分布(图4c)既能够保持传统子波Wigner-Ville分布(图4b)的高时频分辨率,又避免了交叉项的干扰。

图4 匹配子波与传统子波WVD的对比[24]a 合成地震信号; b 传统子波Wigner-Ville分布; c 匹配子波Wigner-Ville分布

利用匹配追踪得到高精度时频谱后,便可开展与之相关的属性分析、储层预测等工作[50]。

3.2 薄储层预测及尖灭线识别

对楔形尖灭模型分析发现:①薄层反射的峰值振幅近似与薄层厚度成正比;②地层较薄时,反射信号峰值频率较高,随着地层厚度的增加,峰值频率逐渐降低;③瞬时谱最强能量所对应的时间厚度随频率增加而减小,逐渐向楔形体的尖灭端移动[30]。根据上述规律,利用匹配追踪方法获得目的层段井旁道时频谱特征并加以分析,便可以有效区分砂泥岩,进而实现薄储层预测[51]。砂泥岩尖灭线是砂岩向泥岩过渡的位置,在尖灭线附近,砂岩逐渐变薄甚至消失,泥岩逐渐增多。利用匹配追踪方法获得的高精度瞬时谱,分析地震信号的振幅和频率响应特征,可有效识别三角洲砂岩尖灭线。

图5为利用本文方法识别出的某工区东三段Ⅱ期三角洲砂岩尖灭线。利用识别出的尖灭线,确定了本区第Ⅱ期三角洲砂体的分布范围(图5中虚线区域),该三角洲东侧被北东—南西向断层封堵,向西逐渐尖灭,这也是西部各井没有钻遇砂岩的原因[30]。

图5 利用匹配追踪方法识别三角洲砂岩尖灭线

3.3 地震数据分频处理

匹配追踪方法利用匹配子波构建同频率剖面,可以方便地实现地震资料的分频处理[33]。经匹配追踪分解后,将所有匹配子波按照其对应的频谱叠加,并沿给定的频率fj抽取,便可得到分频剖面DF(t,fj):

(21)

式中:Gγn(λ)为匹配子波gγn(t)的频谱;λ为积分变量;an为各匹配子波的振幅。

图6给出了不同方法得到的分频剖面。其中图6a 为原始地震剖面;图6b、图6c和图6d分别为Morlet小波变换、匹配子波重构以及按照(21)式得到的分频剖面。由图6可见,小波变换方法难以避免滤波造成的谐波效应,使得分频剖面中存在平行同相轴假象;匹配子波重构方法使得分频剖面出现同相轴错断,不利于地质特征的保持;而按照(21)式得到的分频剖面既不产生平行同相轴,同时又能保持地震剖面的反射特征[33]。

图6 采用不同方法得到的30Hz分频剖面[33]a 原始剖面; b 小波变换分频剖面; c 匹配子波重构分频剖面; d 按照(21)式得到的分频剖面

3.4 噪声压制

基于匹配追踪的噪声压制原理是:先将地震信号进行自适应匹配追踪分解,得到一系列匹配子波和残差,之后依据有效信号和噪声(包括随机噪声及面波)在主频、能量以及时间范围的差异,有针对性地将噪声匹配子波和残差剔除,然后将挑选出的匹配子波进行重构,便可得到噪声压制后的地震信号[35-37,52]。

3.5 强反射剥离

在地震记录中,煤层、不整合面、碳酸盐岩发育的位置通常表现为强反射特征[40-41],这种强反射极易屏蔽其相邻砂体的反射信息,从而导致此类储层无法被有效识别。

匹配追踪利用匹配波形相减法可以很好地剥离强反射,增强储层弱信号,为后续地震储层的预测提供有利数据[42,53-55]。匹配波形相减法剥离强反射的效果与强反射匹配子波的准确度息息相关,匹配追踪所使用的Ricker子波或Morlet小波并不能与实际复杂的强反射波形很好地匹配,而由测井和井旁道标定得到的反射波形与强反射具有更好的吻合度,因此利用井标定波形内插获得各道强反射匹配子波,然后再进行匹配追踪。图7给出了某工区利用匹配追踪法剥离煤层强反射的应用结果。其中图7a为原始地震剖面,剖面中的强反射同相轴为煤层发育带,煤层强反射使得砂体的反射被屏蔽,很难进行后续的储层预测工作,因而需要去除强反射;图7b给出了利用井内插子波进行匹配追踪预测出的煤层强反射;图7c给出了利用匹配波形相减法剥离强反射后的地震剖面。由图7c可见,煤层强反射被剥离后,砂体反射清晰、波组变化自然,有利于识别砂体储层。

图7 匹配追踪剥离强反射[42]a 含强反射的地震剖面; b 利用井内插子波进行匹配追踪预测的强反射; c 强反射剥离后的剖面

3.6 Q值提取、吸收补偿及频散校正

地层Q值与地震子波的传播时间t、频率f存在如下关系:

(22)

式中:A0为未衰减的地震波振幅;A为衰减后的振幅。根据上述关系,将匹配追踪与对数拟合相结合便可提取地层Q值[38]。将匹配子波按照(22)式变换为:

(23)

式中:a=-π/Q;b=lnA0。在得到最优解a*、b*后,便可计算地层Q值:

(24)

将地震波传播的衰减因子定义为:

(25)

公式(25)中指数的实部代表振幅衰减项,虚部代表速度频散项;f0为参考频率。

由于衰减因子是时间和频率的函数,因此可以利用衰减振幅与时间和频率乘积之间的关系进行补偿[39]。首先,利用匹配追踪技术将地震信号分解成一系列匹配子波,将各匹配子波的中心时间和频率的乘积tifi以及各自的振幅投影到坐标平面内;然后将tifi等分,计算各等分区间的平均振幅,根据平均振幅构建出振幅衰减曲线α(fi,ti);最后利用此振幅衰减曲线补偿各个匹配子波的振幅值,将经过振幅补偿后的匹配子波进行重构,从而实现地层的吸收补偿。

对于速度频散问题,可采用(24)式拟合斜率得到地层品质因子值,然后利用公式(25)的虚部进行频散校正。

3.7 剩余时差校正

经动校正和静校正等处理后,地震道集或多或少会存在剩余时差。剩余时差的存在会导致叠加信号的能量消减,从而降低叠后地震剖面的分辨率。

利用匹配追踪进行剩余时差校正,只需对各匹配子波按照其剩余时差进行相应的时移即可[43]。对于各匹配子波剩余时差的求取,需要借助参考道的匹配子波加以确定。假设任一地震道分解的某个匹配子波中心时间为t1,在参考道上以t1为中心的小时窗内搜索最近的匹配子波,假设中心时间是t2,那么此匹配子波的剩余时差Δt=t2-t1,校正后的中心时间为t2,与参考道的中心时间对齐。运用该剩余时差校正策略对地震道集的每道分解的各个匹配子波都进行校正,然后将校正后的各匹配子波进行重构,即可得到剩余时差校正后的地震道集。

3.8 子波拉伸校正

在地震数据处理过程中,动校正和偏移处理都会引起非零偏移距数据出现子波拉伸现象,尤其是中远偏移距的地震数据。子波拉伸致使地震子波畸变、地震数据分辨率降低,不利于进行地震振幅随偏移距变化(AVO)分析。

从本质上讲,子波拉伸只是地震子波波形的拉长,对子波振幅、相位等参数并不影响。根据这一特点,利用匹配追踪校正子波拉伸现象,只需以近偏移距参考道分解的匹配子波为标准,按照临近匹配原则,对中远偏移距分解的匹配子波进行波形压缩即可[46]。

设中远偏移距任一地震道分解的一个匹配子波为gγ1,以gγ1的中心时间为起点,在参考道上搜索最邻近的匹配子波,记作wγ1,对匹配子波gγ1的拉伸校正只需将其压缩成与wγ1等宽即可。运用此子波拉伸校正策略,对地震道集内所有地震道匹配追踪分解得到的匹配子波都进行拉伸校正,再将拉伸校正后的各匹配子波进行重构,即可得到拉伸校正后的地震道集,完成子波拉伸校正。

3.9 反射系数反演

在地震勘探中,直接使用匹配追踪技术对地震信号进行自适应分解,可获得时变子波和对应的反射系数。为得到高分辨率的反射系数,根据奇偶分解理论构建超完备奇、偶匹配子波库,利用匹配追踪分解求得反射系数序列[44,56]。据奇偶分解理论,反射系数可以写成奇、偶脉冲分量的线性组合,与给定子波g褶积后,可产生(26)式分解的地震响应f(t):

(26)

式中:ro为反射系数奇分量;re为反射系数偶分量;g*re、g*ro分别为奇、偶匹配子波,“*”表示褶积运算;an,m、bn,m分别为奇、偶匹配子波对应的系数。由此,超完备奇、偶匹配子波库可由一系列具有不同延时、不同时间厚度的奇、偶匹配子波构建。之后将地震信号在超完备奇、偶匹配子波库中分解,将分解得到的系数an,m、bn,m进行组合重构,可得该地震道对应的反射系数序列。

4 认识与展望

匹配追踪是一种零范数字典学习方法,在地震数据稀疏表示方面具有独特的优势。将匹配追踪技术巧妙地应用到地震资料处理解释的不同环节,根据具体问题设计匹配子波母函数、匹配子波库和匹配追踪分解算法,可以充分发挥匹配追踪技术的优势,对现有地震资料处理及储层预测技术进行更新换代,甚至形成一系列独特技术。该技术的主要发展方向及潜在应用有:

1) 新一代高精度时频分析技术。匹配追踪时频谱比其它技术具有更好的聚焦性,利用匹配追踪时频谱,可以提取分辨率更高的时频属性,为尖灭线刻画、烃类检测、甜点预测、流体可动性判断提供更有利的数据提取与分析手段。

2) 强反射剥离、弱反射增强、频带拓宽等一系列目标处理技术。匹配追踪能够将地震数据分解成线性无关的匹配子波组合,对这些匹配子波的振幅、时移、频谱特征进行统计和调整,然后再重构,以实现目标处理。

3) 地震道集优化技术。地震道集存在信噪比低、同相轴随偏移距增大而变宽、深层大偏移距数据由于地层吸收而存在振幅衰减等问题。根据不同问题的产生机制创建各自相应的匹配子波库,利用匹配追踪技术进行噪声压制、吸收补偿、拉伸校正等处理,从而实现地震道集的优化。需要说明的是,目前的很多处理技术需要计算子波的逆,但逆算子通常不稳定,需要加白噪或阻尼;而匹配追踪不需计算子波的逆,因此处理过程稳定。

4) 地震稀疏反演技术。利用匹配追踪的零范数字典学习能力,可以很方便地将其应用到地震反演过程中,无论是叠后波阻抗反演还是叠前AVO反演。还可以将匹配追踪技术应用到全波形反演、各向异性反演或螺旋道集(OVT)反演中,当然首先要解决计算效率问题。