干燥物系的特征函数及其理论解

李长友

（华南农业大学南方农业机械与装备关键技术教育部重点实验室，广州 510642）

0 引 言

干燥是动量、热量、水分3种传递同时作用的过程，动量传递可由牛顿黏性定律描述；热量传递可由傅里叶定律描述，而水分传递称为扩散，可以由费克定律描述。3个定律客观地从理论上描述了物系单一行为的传递现象，依此为基础，人们把水分迁移假设成连续介质流动，基于时间和空间的连续函数，采用欧拉方程、拉格朗日方程、体积平法等，围绕表征物系性质和过程特征的进行了大量的模型试验理论研究，由试验数据，给出了针对特定物系多种形式的计算模型[1-3]。由于流动过程不存在严格的牛顿流[4]，依赖浓度的扩散系数没有数学解[5]，热传递过程物性动态变化的内部因素与外部条件双向作用，很难揭示热传递系数的变化规律。3个定率应用时，除必须满足各自的单值性条件外、还要尽可能满足其几何条件、物理条件、时间条件和边界条件等。在模型求解时，必须把过程的综合因素归结为常系数才能进行，因此，不能保证积分结果与实际完全一致。基于扩散动力学建立的物料干燥模型，存在活化能、指前因子和过程指数难以定量等问题[6]，如何获得干燥过程的分析解是长期以来干燥理论研究的重要命题。

干燥是物料水分蒸发的自发过程，干燥动力变化范围在水的饱和蒸汽压与外部的水蒸汽分压力之间。无论何种物料，在何种外部约束条件下，干燥的动力都是源自于水的饱和蒸汽压，它是汽化温度的单值函数[7]。干燥所能到达的极限，是物料水分活度在数值上等于外部介质的相对湿度的平衡含水率状态点，而状态变化取决于干燥的广度和强度，广度与去除的水分量成正比[8]，在数值上等于物料含水率与其平衡含水率之差；强度用干燥速率来表征。为了揭示干燥状态变化规律及其发生的机理，研究人员针对不同物料，建立了干燥速率、升温速率、质构变化（收缩与变形）规律、质量与品质的变化等多种干燥模型[9-10]。按照唯象理论和体积平均理论[11]，建立扩散微分方程[12-13]，基于抽象的不可逆热力学函数来表达水分扩散现象，预测干燥速率，确定干燥时间，分析实际过程，指导工艺设计和优化过程控制[14-15]，但没有揭示模型中计算系数的物理意义[16-17]。

基于质量、能量守恒定律和不可逆热力学原理，Philip和Devries把物料内部质量传递区分为毛细管流动和蒸汽扩散运动2种情况，基于温度、浓度和压力3种势场，建立了各种干燥微分方程组[18-22]，基于孔道网络模型的模拟手段[23-24]解析干燥过程并展开了一系列扩散模型及其计算系数的研究[25]，在假设蒸发面由物料外表面向内退缩，蒸发面积逐步减小等条件下，解析降速干燥过程[26-28]。以汽化界面为分界面，把物料干燥状态，简化成界面内部为湿区，界面外部为完全处于平衡态的干区，并认为湿区的相对湿度为100%，且水分汽化只发生在干区和湿区的交界面上，给出了诸多解析特定物料干燥过程的扩散模型。由于干燥是在湿、热和动态变化的物性参数等多种因素作用下的非线性自发过程，伴随去水，物料自身的物理性状实时改变并发生复杂的理化、生化反应，体积收缩、质构变化会引起空隙、迂曲度改变，导致水分传递路径及强度发生改变，都使实际过程与理想化的分界面扩散不一致[28-32]，这是把实际过程归结成常系数扩散，建立模型时的共同缺陷[33-35]。

影响干燥现象的因素繁多，但一切因素综合作用的结果，完全反映在水分蒸发，而能否蒸发要取决于物料水分的活度。活度是温度、物料含水率的函数。近年，笔者以水分活度变化为物料干燥状态的统一特征，明确了干燥是水分汽化对外做功的自发过程，汽化现象的标志是呈现功的输出，这个功源自于物系的自由能，基于自由能变化，给出了物料水分的结合能解析式[36]，得到了物料水分汽化潜热系数的数学解[37-38]。在此基础上，本文以水分活度为物料干燥的统一特征，以自由能传递和转换为统一尺度，按照能量平衡原理，对应外部约束条件，建立具有普遍意义的干燥物系特征函数并给出理论解，揭示干燥物系的机理函数。

1 干燥物系的过程特征

1.1 干燥特性

按照水分与物料的结合形式，可以把干燥区分为非结合和结合水分蒸发两种情况。非结合水，不受物料的作用，相当于自由液面蒸发，结合水分是存在于物料中的水分，蒸发受物料的影响，作用的结果完全取决于物料自身的物理性质。与其对应的干燥特性如图 1所示。非结合水的水分活度等于1，蒸发速率取决于外部条件；而结合水与干物质组分间存在结合能，水分活度小于 1且在干燥过程中随含水率降低而减小，在稳态介质条件下，蒸发速率是物料水分活度的函数。

图1 干燥特性曲线Fig.1 Drying characteristic curve

1.2 干燥系统

干燥是湿物料与外部介质，通过边界进行能量和质量传递与转换的开口系统。在此，用符号pe和p分别表示介质和物料中的水蒸汽分压，用ps、pv和φ分别表示饱和蒸汽压、汽化后的水蒸汽在物料内部的分压力和水分活度，用T和μ分别表示汽化温度和物料水分的结合能。简化的干燥系统如图2所示。

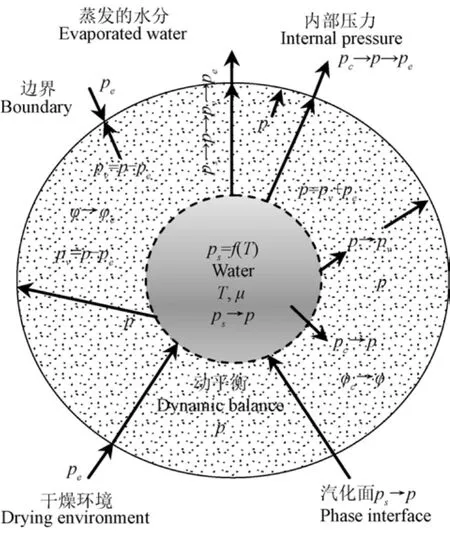
图2 干燥系统Fig.2 Drying system

1.2.1 系统状态参数及其变化

物料内部水分蒸发经历由汽化面蒸发、扩散到系统边界，然后进入介质的过程。在汽化面内部及汽化面上的水蒸汽压是饱和蒸汽压ps，ps与物料无关，它是温度T的单值函数，是水蒸汽的最大动力极限。由于物料水分蒸发受结合能的影响，结合能降低了蒸发面上方的水蒸汽分压力，使水蒸汽迁出的动力减小，从而在汽化面的上方呈现的压力是p，转变的位置发生在汽化面上方，所以，p是水分汽化迁移的动力。

由于气体压力波传播的速度很快，物料含水率的变化速率远远小于气体分子的压力波传播速率，所以，当干燥过程中系统外部的水蒸汽分压力恒定不变，物料内部的水蒸汽分压力则是经历无数中间状态，由初始的水蒸汽分压力pc→pe的准平衡过程。

当介质中存在水蒸汽分压力pe时，这个压力直接作用在系统的内外。那么，汽化份数，在物料内部与介质中的水蒸汽相混合的过程中，则会使其压力由p状态变成了pv状态。变化的幅度则是取决于pe的大小，即pv=p-pe，pv是蒸发份数迁出物料的最终动力。

由此可见，物料蒸发出的水蒸汽状态变化是的过程的状态变化发生在汽化面上。的状态变化过程是由汽化面到系统的边界，即物料的内表面。迁出物料后，趋向于pe。

当pe=0时，干燥则没有外部水蒸汽分压的影响，干燥过程完全取决于物料自身，所以，在pe=0的条件下，便可完整地解析出物料水分的结合能。

由于p的值取决于物料水分的活度，它是一切物料水分的共同属性。在干燥过程中水分活度随含水率的降低而减小且是连续变化的。变化的规律体现在水分结合能大小和混合后的pv值。基于水分活度ps→p，和p→pv的压力状态变化及其发生的位置和区域，按照水分活度φ=p/ps，即可解析出物料内部的水分活度分布，进而，由实际去水的广度和任意一个对应水分活度为φ状态点的去水强度，即可得到实际干燥过程的理论解。

2 水分蒸发自由能平衡方程

2.1 自由能传递与转换理论表达式

干燥现象可以由水分迁移的数量与其迁移势之积来表达，完全取决于物系的状态参数，而一切过程只要是取决于热力状态参数的能量都全部归结为焓[7]，所以，无论水以何种形式存在于物料中，也无论干燥的一切机理参数如何变化，干燥现象都可以由状态函数来表达。因此，在任何条件下，干燥过程的任一状态点的热能消耗都可依据该状态点的焓来计算。基于吉布斯-亥姆赫兹自由能概念，得到1 kg水分定压汽化过程的热力学第二定律的数学表达式（1）或式（2）

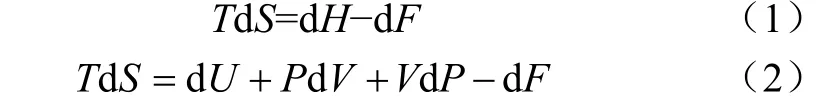
式中T是热力学温度，K；S是熵，kJ/K；H是焓，kJ；P是压力，Pa；V是体积，m3；U是内能，kJ；F是自由能。kJ。

水在自由状态下定压汽化时，不产生轴功，式（2）中的VdP项等于 0，于是得到水在自由态定压过程中的自由能表达式（3）[8,36]。

水在物料中汽化时，结合能降低了蒸发面上方的水蒸汽分压力，相应地减少了水分的自由能，自由能减少的量在数值上相当于汽化过程所做的技术功（轴功）。此时，式（3）中的VdP项不等于 0，在此，用符号Fg表示汽化份数，汽化时的自由能消耗，得到物料水分，定压汽化时的自由能消耗表达式（4）。

式中的VdP是克服水分结合能所做的轴功，其值等于迁移势与质量之积，在数量上，与汽化份数的质量成正比，可由式（5）计算[8,38]

式中的dM是汽化迁移的水分量微元，kg，负号表示迁移的方向沿质量减小的方向。μ是水分的质量迁移势，kJ/kg，即汽化1 kg水分克服结合能所做的功，在理论上可表达

式中Md是除水分以外的其他组分，在此称其为绝干物质质量，kg。

由式（1）知，dF=dH−TdS，自由态的水，定压力汽化时，式（2）中的VdP项等于0，d(PV)=PdV，由于P和V都是状态参数，源自于系统的热能，热能在任何情况下都可以用一个平均过程比热与其温差之积来表达，在此，用符号Rpn，表示在[273.15,T]温度区间，水分汽化，自发流动趋向终态平衡过程中，自由能转化为单位质量流体温度变化1 K的热能平均值，并称其为水分汽化过程特征常数，kJ/(kg·K)，它的物理意义等同于水分汽化过程的平均定压比热，可以由中值定理和压力函数与其原函数（自由能传递和转换）得到证明。由此，对应定压汽化条件，得到从物料内部每迁移1 kg水分时，自由能转化的功，这个功在数值上等同于水同物料的结合能，即dμ=-vdp=RpndT，积分得到解析式（6）[36]。

式中φ是水分的活度（小数），Rpn是以三相点为基准，水分汽化温度[273.15,T] 的区间特征常数，kJ/(kg·K)，p是水蒸汽的分压力，Pa，ps是饱和蒸汽压，Pa。

用小写字母v表示比体积，m3/kg，h表示比焓，kJ/kg，f表示比自由能，kJ/kg，得到1kg水分在自由态和物料中汽化时的自由能消耗微分式（7）和式（8）

由于同温度下水蒸汽的比体积远大于水的比体积，二者相比，水的比体积可以忽略不计，于是，求积得到 1 kg水分在自由态汽化为理想气体时，消耗的比自由能表达式（9）。

把式（6）代入式（10），得到物料水分汽化时的比自由能消耗表达式（11）

式（11）表明，在确定的温度区间，水分蒸发的自由能消耗量，是绝对温度和水分活度的状态函数，式（11）适合任何物料，具有普遍意义。在此，用符号Cz表示1−lnφ项，并称其为自由能消耗系数，得到表达式（12）。

式（12）表明，当水分活度等于 1时，自由能消耗系数等于1，存在水分结合能时水分活度小于1，此时的自由能消耗系数大于1。表征从物料中汽化同样数量的水分消耗的自由能是自由态时的1−lnφ倍。

2.2 蒸发过程的自由能平衡方程

假设在水分活度等于1时，物料的干基含水率为M0，%。对应介质条件的平衡含水率为Me，%。分别用符号区间上的最大汽化速率和干燥速率，%/h；那么，小的量，则等同于物料约束水分蒸发多消耗的自由能，由此得到式（13）所示的自由能消耗平衡关系式，化简式（13）得到物料自身固有的干燥速率比状态函数表达式（14）。

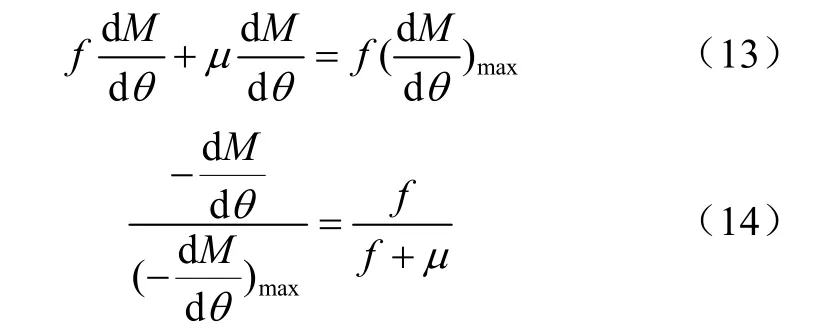
把式（6）和（9）代入式（14），得到干燥速率比状态函数表达式（15）

式中θ是干燥时间，h。

式（14）和式（15），表征的是物料经历准平衡过程所能实现的理论干燥速率。式（15）中的表达的是物料在理想绝干介质中，稳态干燥的情况，是物料自身固有的干燥特征函数之一。

由式（15）可以看出，干燥速率比与成正比，它是在外部介质相对湿度等于 0的条件下得到的，是干燥速率比随水分活度变化的一般关系式，它是强度量之比等同于质量比。由式（14）知，这个比值又等同于自由能比，所以，无论何种物料，只要其水分活度相同，汽化相同数量的水分克服结合能做功的自由能消耗必然相等。因此，式（15）可以用来评价干燥物系的理论热耗，但干燥速率与外部介质条件和物料内部含水率分布有关，水分汽化后的运动和状态变化与外部介质的含湿量有关，在解析实际过程时，应基于图 2揭示出蒸发份数在相应的外部介质条件下，汽化、混合过程的阻力特征，其自由能消耗要基于式（22）来定量。

2.3 理论干燥速率比变化特征

在外部介质相对湿度等于 0的干燥过程中，任何物料的干燥速率比都是其水分活度的单值函数。那么，对应[1,0）的水分活度变化区间，基于式（15）解析出的干燥速率比随水分活度的变化规律如图3所示。

图3 干燥速率比的变化Fig.3 Change of drying rate ratio

水分活度反映物料水分结合程度和水分迁出时的受阻情况，体现在物料水分迁移受到干物质组分的阻力而消耗的自由能，由图 3看出水分活度值越高，干燥速率比越大，表明结合程度越低，与干物质间的结合能越小；而水分活度值越低，结合程度越高，与干物质间的结合能越大。在水分活度趋向于0时，干燥速率比也趋向于0时，此时水分活度的微小变动，会引起干燥速率比的较大变化。

2.4 物料水分活度计算式

水分活度取决于物料的含水率和温度，是物料自身固有的状态函数之一。在稳态条件下，平衡含水率是物料干燥所能到达的极限，是物料完全回归环境态时的含水率。针对不同种类的物料，不同国家的研究机构和学者，给出了多种平衡含水率计算式，并称其为平衡含水率模型[39-42]。

由于平衡含水率可在静态试验条件下正确测量，对应不同的物料已有较为精确的计算式。式（16）是国际上普遍采用的平衡含水率模型之一，模型中计算参数如表1所示[37]。

式中A、B、n为计算系数。

表1 几种粮食平衡含水率模型中的系数值Table 1 Coefficients in several models of grain equilibrium moisture content

平衡含水率是状态函数，对于所有物系，在理论上均可表达为Me= [f(T,φ)]e，下标e表示的是相平衡条件，基于式（16），得到干燥介质的平衡相对湿度φe表达式（17）。

在相平衡条件下，物系中各点的迁移势均等，质量迁移梯度为0，物料内外的温度、压力平衡，各个状态参数都不随时间变化，那么，在相平衡条件下，水分活度在数值上则等于介质的相对湿度，其值可以由介质的温度和相对湿度计算。根据热力学分析问题的一般方法，将干燥现象看作是从一个平衡状态趋向另一个平衡状态的过程。于是，对应物系相平衡过程的物料水分活度就可表达为式（18）。

式中T是物料温度，K，φ是水分活度，M是含水率，%。式（17）和式（18）中的 2个自变量分别是物料含水率和温度，这2个参数都是干燥物系的状态参数，但式（17）和式（18）的物理意义不同，物料水分活度是自身的状态参数，是取决于物料温度和含水率的状态函数，而介质的相对湿度是介质温度和湿含量的状态函数。

2.5 单位自由能及最大干燥速率比变化规律

单位自由能消耗是指从物料中每蒸发1 kg水，物料消耗内能使水蒸汽运动而具有对外做功能力的那部分能量，单位是kJ/kg。在理论上，它是每蒸发1 kg水，可向外输出的技术功。由式（1）或式（2）知，它是内能转化的技术功。基于式（11）、式（12），式（18）和式（15）解析的不同温度条件下，小麦干燥状态函数的变化规律如图4所示。

图4 小麦干燥状态函数变化规律Fig.4 Change rule of drying state function of Wheat

水分汽化时的单位自由能消耗随含水率的变化规律如图4a所示，水分活度随含水率的变化如图4b所示，自由能比随含水率变化如图4c所示，干燥速率比随含水率的变化如图4d所示。

从图4a看出，小麦降速干燥过程的单位自由能消耗随含水率的降低而增大，且含水率越低增大的幅度越大，其影响明显高于温度的影响，但当含水率高于25%以后，在不同干燥温度条件下的自由能变化与温度间的关系趋于确定的常数，且是温度越高，其值越大，此时的物料水分的自由能变化可以看作是温度的单值函数，水分的汽化过程则等同于自由液面蒸发。

自由能比无量纲，是一切物料状态变化的共同属性。在水分活度等于1时，自由能比等于1，存在水分结合能时，水分活度小于1，自由能比大于1且随水分活度的减小而非线性增大。

无论何种干燥工艺系统，物料的干燥过程都必然存在对应其降水期间上的最大干燥速率状态点，在相同的介质条件下，该状态点必然是水分活度的最大点。由式（11）知，RpnT在对应的温度区间[273.15,T]上是常数，所以，以三相点为基准点，在任意一个温度区间内，干燥过程自由能的变化，在理论上都可以用水分活度来解析。基于水分活度与温度和含水率间的关系式（18），便可得到任意温度区间[273.15,T]上的自由能比的变化规律。

物料水分活度也是无量纲，其变化区间是(0,1]。从图4b看出，在同一水分活度下，不同温度条件下的含水率差的变化规律是沿0到最大，然后再趋向于0的过程。同样，在同一含水率条件下，不同温度条件下的水分活度差的变化规律也是沿由0到最大，然后再趋向于0的过程。小麦含水率在 30%以上时，水分的活度非常接近自由态，而在含水率低于5%以后，水分活度很小，且随含水率的降低非常缓慢，表明物料对水分的牵制力随含水率降低而迅速增大，且是非线性过程。

图4c是不同温度条件下，小麦水分汽化时的自由能比随含水率变化。由图4c看出，在任何温度条件下，小麦水分汽化时的自由能比随物料含水率的降低而增大，而在相同的含水率条件下，温度越高，自由能比越小，表明提高温度，相应地增大了干燥动力，相对降低了物料水分汽化时的自由能消耗。

干燥速率比是无量纲，对于 2个几何相似的干燥工艺系统，在物料水分活度或者物料水分活度与介质相对湿度差相同的条件下，则对应干燥速率与其同等条件下的最大干燥速率之比必然相等。干燥速率比越小，表明物料与水分间的结合能越大，这是物料自身固有的内在属性。由于式（15）对应的是介质相对湿度等于 0时的情况，所以，它揭示的是物料自身固有的理论过程，是表征一切物料的干燥过程的一般关系式。无论水以何种形式存在于物料中，也无论干燥的一切机理参数如何变化，干燥现象都可以由其干燥速率比状态函数来表达。图4d是解析的不同温度条件下，小麦的干燥速率比随含水率变化规律。从图4d看出，在同一理论干燥速率比下，不同温度条件下，含水率差的变化是沿由 0到最大，然后再趋向于 0的过程，同样，在同一含水率条件下，不同温度条件下的水分活度差变化也是由 0到最大，然后再趋向于0的过程。含水率在25%以上时，理论干燥速率比的变化很小，而在 25%以下时，干燥速率比较快地降低，在相同的含水率条件下，温度越高，干燥速率比相对越高，但当含水率降至约5%以后，温度对干燥速率比的影响明显减小。图4d中各曲线间的纵坐标差和横坐标差的变化，清晰地呈现了小麦的干燥过程同时受温度和含水率的影响这一客观事实。解析结果，为实现高效节能干燥，依据物料的干燥状态，合理地匹配干燥条件参数，提供了理论依据和解析的新方法。

比较图4中a、b、c和d图中的曲线，不难发现，小麦在含水率在 25%以上时，温度和含水率的变化对比自由能消耗，自由能比，水分活度和干燥速率比的影响都很小，表明当物料处于高含水率状态时，水分活度接近于1，自身拥有较大的去水动力，提高温度对干燥过程的影响并不显著。随着含水率降低（如图4d中的25%～10%含水率段），温度和含水率的变化对比自由能，自由能比，水分活度和干燥速率比的影响较大，且均为非线性变化，此时，提高干燥温度，能够明显地增大自由能、水分活度和干燥速率比，降低自由能比，强化干燥过程。

3 干燥特征函数及其理论解

3.1 蒸发过程中的技术功

在实际干燥过程中，物料内部存在的含水率偏差，不同位置上的水分活度不一定相等，对应水分活度，所呈现的水蒸汽分压力也不一样，在汽化面内的压力状态变化是由，由汽化面到边界面混合区间的压力变化是由。

由图 2知，物料水分汽化经历汽化和与汽化面上方水蒸汽混合两个连续变化的过程。当介质中的水蒸汽分压力不为0时，水分蒸发不仅要克服结合能做功，同时，还受外部介质中的水蒸汽分压力的影响，而使汽化的水分量减少，此时，蒸发份数，由汽化面运动到边界面的实际压力变化范围是[ps-pe,p-pe]。在此用F(μ)表示，汽化份数克服结合能做功消耗的自由能原函数，服从式（7），基于压力函数与其原函数（自由能）间的关系，其消耗的份额则服从C1是积分常数。当pe=0 时于是得到

水分汽化后与汽化面上方的水蒸汽混合，其压力变化同样是连续过程。就物料水分汽化微元体上压力而言，汽化所呈现的压力是初态压力pc，而汽化面上方的水蒸汽压力是p，当外部介质的水蒸汽分压力为pe时，蒸发份数则随pe的增大而减少，所以，蒸发份数呈现的压力变化范围是[pc-pe,p-pe]。在此，用符号F(p)表示混合过程中，压力函数的原函数（自由能），那么，该过程所消耗的自由能份额则服从F(p) = -vdp+C，C是混合22区间的积分常数。当pe=0时，F(p)=0，于是得到

在此用符号μx表示蒸发份数相对于自由态蒸发 1kg水时的自由能减少量，并称μx为同比自由能消耗，单位是 kJ/kg。那么，μx则是F(μ)与F(p)两项之和，即μx=F(μ) +F(p)，于是，得到积分式（19），求解得到μx的解析式（20）。

自由能消耗，是自发过程物系减少内能转化为技术功的度量，式（20）表征的是水分从物料中蒸发时与在自由态下汽化1 kg水相比，多消耗的自由能。由式（14）知，消耗的自由能增加，等同于蒸发的水分量减小，呈现干燥速率降低。基于的式（14）和式（15），得到对应不同介质条件的干燥速率比表达式（21）和式（22）

式中φe是干燥介质的相对湿度（小数），φ是对应物料含水率为M时的水分活度（小数），φc是物料的初始水分活度（小数）。

式（22）是状态函数，其值取决于物料的初始水分活度、水分活度和干燥介质相对湿度（物料平衡水分活度）；它是基于水分活度表达的的一般性关系式，反映的是一切物系中，物料和介质交互作用的情况。由于干燥是水分单一组分汽化、迁移的物系，而水在相平衡条件下的汽化压力是饱和蒸汽压，所以，这个压力就是汽化面内蒸汽压，它是温度的单值函数。汽化后（蒸发份数），在与蒸发面上方的水蒸汽混合过程中的压力变化经历的是由对应初态水分活度时的压力pc趋向于给定的外部介质中的水蒸汽分压力（平衡压力）的状态变化过程。

因为物料内部含水率偏差消失的速率很缓慢，与水蒸汽压力波传播的速率相比，可以忽略不计。物料在相平衡条件下，其水分活度在数值上等于介质的相对湿度，即，由此可见，在同一温度条件下，水蒸汽分压力与水分活度一一对应，基于相平衡条件下试验得到的物料水分活度，能够客观真实地反映其对应的水蒸汽压力，那么，基于物料内部不同位置上的压力变化，则可客观地反映出所处位置的水分活度变化，这样一来，按照图 2所示的蒸发过程中，不同位置上的压力值及其在汽化、混合过程的状态变化，就可以解析出内部的水分活度分布及其含水率偏差。

3.2 干燥速率特征函数的理论解

3.2.1 最大汽化速率常数

不同的物料在不同的干燥工艺和介质条件下的干燥特性不同，但对于特定的物料，在特定的干燥工艺和介质条件下，对应其干燥区段，均存在相应的干燥速率最大值，且发生在物料内部水分均匀一致（物料内部无水分偏差）的情况下，把此时且水分活度等于 1时的干燥速率称为最大汽化速率，并用符号C0表示，kg/h。基于式（22），得到C0的计算式（23）。

3.2.2 干燥机理函数的理论解

物料在干燥过程中所能去除的水分称为自由水，在平衡状态下所含的水分称为平衡水。在此，用符号M0、M和Me分别表示物料的最大极限含水率、含水率和平衡含水率，自由含水比则被表示为(M−Me)/(M0−Me)。基于浓度扩散，干燥速率则正比于含水率差，即(M−Me)，在此用k表示干燥常数，h-1，按照菲克定律，在[M0，Me]含水率区间内，干燥速率和最大汽化速率可表达为式（24）和式（25）[6]。

式中M是物料的干基含水率，%，M0和Me分别是极限含水率（水分活度等于1）和平衡含水率，%，k是干燥常数，h-1。

用式（24）除以式（25）得到自由含水比与干燥速率比关系式（26）

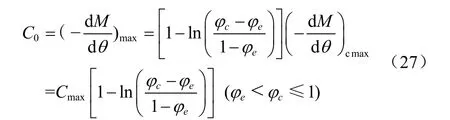
由式（23）、式（26）和式（27）得到对应物料在实际含水率区间M[Mc,Me)上的自由含水比变化的理论表达式（28）

式（28），表征物料干燥的机理，在此用f(φ)表示的变化规律，于是，得到干燥机理函数的数学表达式（29）。

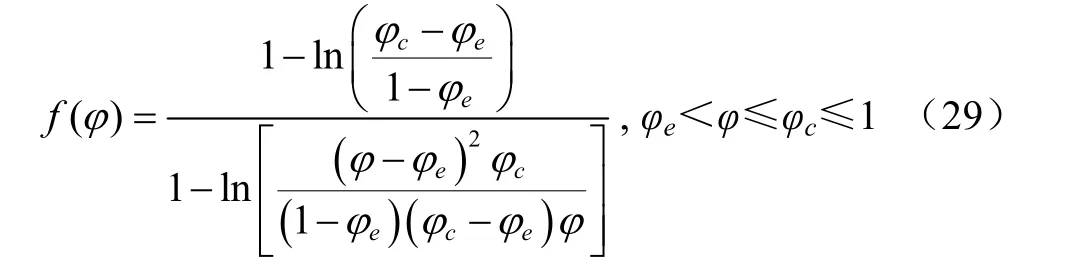
3.2.3 干燥速率的理论解

用式（28）中的含水率对物系的水分活度求微分得到关系式（31）

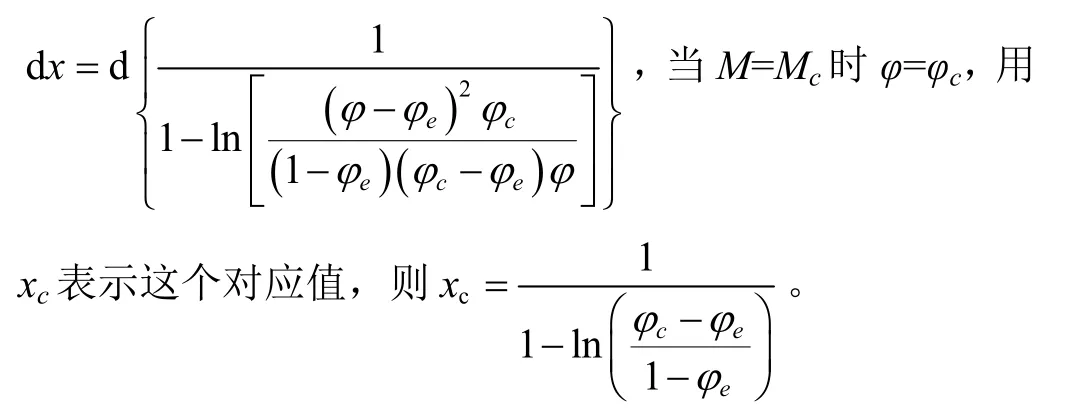
把式（31）中的dM代入式（30）并变换积分上下限,得到水分活度随时间变化的积分通式（32）。

求解式（32）并把x、xc和式（27）代入后得到物系水分活度与时间的关系式（33）

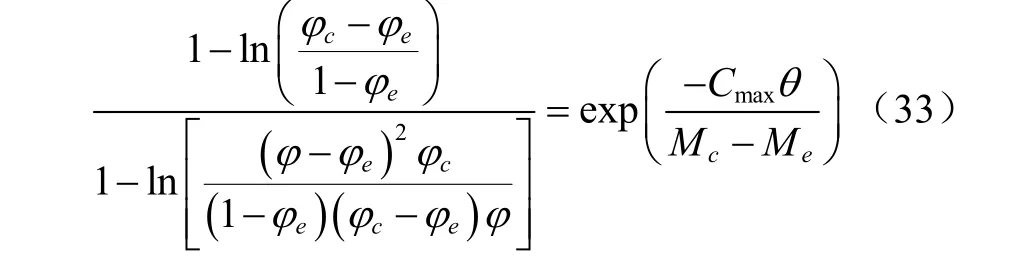
式（33）建立了物料水分活度，初态的含水率，初态水分活度，平衡含水率，平衡水分活度和区间最大干燥速率之间的内在关系。

把式（33）代入式（28），得到基于M[Mc,Me)实际干燥区间的自由含水比理论表达式（34）。

在式（34）中Cmax是实际过程中，M[Mc,Me]区间的干燥速率最大值。式（34）表明在稳态介质条件下，任意物料干燥过程均服从指数模型，在区间[Mc,Me]上，干燥常数的理论解是

由式（34）得到M[Mc,Me]区间的干燥速率表达式（35）

由式（35）看出干燥速率随时间的变化也服从指数模型，其值取决于物料的初始水分活度、平衡含水率、区间最大干燥速率和初始含水率。在物料初始水分活度等于1时，Mc=M0、φc=1，此时，指前因子等于最大汽化速率。

3.3 讨 论

水分扩散，依赖浓度的现象普遍存在，已有诸多关于此方面的通论，气态物质自发迁移的动力是压力的单值函数，是不争的事实，所以，是否存在扩散现象，则取决于是否存在压差。为从理论上对实际过程定量描述、研究人员在等温条件下测量 2种物系的热量比，表征汽化潜热系数比[43]，基于这个比，成功地建立了过程量与状态量之间存在内在联系，但存在的问题是，要得到客观真实的试验测定值非常困难，根源在于熵是抽象的热力学函数，在自发过程中一定存在熵增且在不同过程间的可比性很差，往往导致测量结果偏离实际。

由于一切过程中物系间的相互作用，本质上都是体现在能量的传递和转换，在一切自发过程中，自由焓的变化量，始终服从 dh=cpdT。自由焓的减少量，在数值上就是汽化份数克服物系阻力所输出做的功，所以，以自由能为统一尺度，可以，完整地从理论上解析出实际过程。

对于温度为T，压力为P，体积为V，摩尔量为n的理想气体混合物，服从状态方程PV=nRT。基于道尔顿分压力定律，得到该物系中，各种组分的分压力与总压力之比和其摩尔数与总摩尔数之比，即压力比和摩尔成分或者体积成分间的关系式

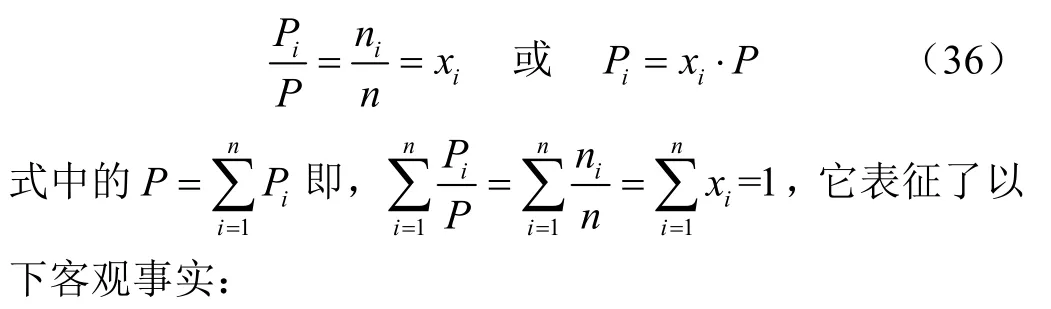
1）道尔顿分压力定律表明了理想气体混合物的总压力等于各组成气体的分压力之和。

2）压力比与气体常数无关，在数值上等于质量成分和体积成分。

3）各组成员的分压力与总压力比（简称压力比）等于体积成分，它与总体积无关。这是因为在同温度同压力条件下同摩尔数的任何理想气体占居的体积都相等，而在任何条件下

4）各组成元的分压力与总压力比（简称压力比）与温度，总体积，总压力，总摩尔数无关，在数值上等于质量比。这是因为摩尔数的值的完全取决于质量，质量成分与温度等其他一切过程因素无关，压力比也是与温度、体积等其他一切过程因素无关的物理量。

由此可见，压力比虽然是基于理想气体建立的，但它具有普遍意义，适合于一般气体质量混合的一切实际过程。

干燥是湿物料与外部介质，通过边界进行能量和质量传递与转换的开口系统。水分汽化，运动受物料和外部介质的双重作用，完全体现在水与绝干物质组分间的结合能和运动的阻力。二者综合作用的结果则完全反映在物料的干燥速率，干燥速率的变化，完全取决于物系中的水蒸汽分压力的状态。而在外部的水蒸汽分压力恒定不变条件下，系统内部的水蒸汽分压力则经历无数中间状态，由初始的的准平衡过程。

当pe=0时，不存在外部水蒸汽分压的影响，干燥过程完全取决于物料自身，所以，在pe=0的条件下，便可完整地解析出物料水分的结合能。对应外部条件，基于压力函数及其原函数（自由能消耗）和相平衡条件下得到的水分活度与其一一对应的压力关系，能够肯定数据的客观性，而按照汽化、混合过程压力变化的位置和区域，解析物料内部的水含水率分布，基于自由能揭示干燥特征函数并得到理论解，无论在逻辑上还是理论上都成立。

4 结 论

干燥物系的自由含水比和干燥速率是对应外部条件，物料水分活度、温度和初始含水率及其分布的状态函数，从理论上揭示了以下事实：

1）无论水以何种形式存在于物料中，也无论干燥的一切机理参数如何变化，干燥现象都可以由其自由能传递和转换来定量表达。

2）基于物料的最大汽化速率C0、初始态水分活度φc、平衡条件下的水分活度φ和介质相对湿度φe，可以从理论上揭示出实际过程干燥速率的变化，其关系是M是含水率，%，θ是干燥时间，h。

3）干燥是物料自身的状态变化过程，它是以外部约束为条件条件，干燥机理函数的理论表达式是

4）在干燥过程中，物料的自由含水比等于干燥速率比且随时间的变化服从指数模型，其理论表达式是干燥速率随时间变化服从最大汽化速率的理论解其中，Mc、Me和Cmax分别是初始含水率、平衡含水率和区间干燥速率特征常数。