协同中继通信系统稀疏信道估计算法研究

张爱华　周其玉　贺博鑫

摘 要：针对无线协同通信系统，采用基于加权零吸引最小均方（Reweighted Zero-Attracting Least Mean Square，RZA-LMS）算法，在信道稀疏度未知的情况下进行信道估计，该算法通过在代价函数的惩罚项中引入基于对数的稀疏约束项，使得自适应过程具有吸引零滤波器系数的能力，通过自适应滤波和最小均方估计可实现系统的稀疏度辨识与信道重构。与其他线性信道估计方法相比，该方法能够有效挖掘并利用无线系统的稀疏结构，进而提高信道估计的性能，算法具备计算复杂度低、易于实现等特点。

关键词：稀疏度感知;协同无线通信;信道估计;零吸引;最小均方算法;系统模型

中图分类号：TP84+2;TN911.72文献标识码：A文章编号：2095-1302（2020）07-00-04

0 引 言

随着宽带无线通信技术的快速发展，移动通信的数据业务量激涨，对未来通信技术中频率效率和能源消耗的需求带来了极大挑战。5G通信技术发展的核心是优化网络结构和网络传输技术，从根本上提高频谱效率和功率效率。基于中继的协同通信系统具有空间分集和复用能力，能够有效提高数据传输容量。未来移动通信标准组织和宽带无线网络标准均将中继的概念引入未来通信标准中，期望系统在有限的发射功率下传输尽量长的通信距离[1-2]。协同通信技术在提高系统数据传输性能的同时，需要解决诸多问题，如协同方式、中继节点的选择等[3]，解决这些问题的先决条件是系统需要获取精确的信道状态信息，因此高性能的信道估计技术尤为重要。

压缩感知理论能够利用信号的稀疏信息，通过很少的观测值进行稀疏信号的有效重构。无线多径信道的冲激响应具有稀疏特性[3]，为了深入挖掘并利用信道的稀疏结构，研究者们利用压缩感知理论，结合通信系统时延域和角域的稀疏特性，开展了稀疏信道感知的研究工作[4-7]。

早期的压缩感知信道估计算法如正交匹配追踪[8]、压缩采用匹配追踪[9]等，该类算法均是作用于系统稀疏度已知的情况，但在实际通信系统中，信道的稀疏度通常未知。稀疏度自适应匹配追踪（Sparsity Adaptive Matching Pursuit，SAMP）算法[10]可以有效重构稀疏度未知的信道，但算法对迭代步长有较高的依赖性，算法在获取较好重构性能的同时，为系统带来了较高的运算复杂度。

近年来，在压缩感知理论的启发下，引入稀疏惩罚思

想[11-14]的自适应滤波算法得到了快速发展。考虑到空间分集系统的信道间存在相关性，而最小均方滤波算法的优点是利用信道间的相关性在非理想信道状态下完成信道重构。因此，为了辨别时变中继通信系统的稀疏度，并利用稀疏度对系统进行有效压缩信道感知，本文引入稀疏辨识的加权自适应滤波算法，該算法能够有效估计稀疏度未知的信道，并具有较低的计算复杂度。理论分析和实验仿真验证了加权自适应滤波方法的收敛性和信道估计的有效性。

1 系统模型与LMS算法

1.1 单中继协作通信系统的信道模型

在放大转发模式的单中继通信网络结构中，系统由源节点S、目的节点D和中继节点R组成，每个终端节点配置单天线且采用OFDM调制解调技术。本文仅考虑“源节点S-中继节点R-目的节点D”链路所形成的级联信道状态信息的估计问题。假设源节点和中继节点的平均功率分别为PS和PR，各节点之间的信道相互独立且为准静态，h1（n）和h2（n）分别代表从S到R，R到D之间的时域离散冲激响应，可以表示为：

式中：ρRZA=μγRZAεRZA，εRZA=1/ε'RZA;|·|表示分段绝对值算子。RZA-LMS通过选择幅度大的信道抽头系数和幅度小的抽头系数进行非零抽头系数的辨识。非零权系数的绝对值不断变小，强迫更多的权系数最终收敛于零，保证了权系数更新值的稀疏特性。该算法对于接近ε'RZA的信道抽头系数具有较强的吸引力，对于|hi（n）|>>ε'RZA的情况，零吸引的效果会减弱，可以除去ZA-LMS算法计算中的有偏误差。在一个迭代周期内，RZA-LMS算法需要进行4L次加法运算和（5L+1）次乘法运算以及L次存储运算，由于引入了加权因子的运算，RZA-LMS算法相比于LMS算法和ZA-LMS算法，运算量稍有增加，但是比l0范数以及SAMP算法，运算量减少了许多。

3 仿真与分析

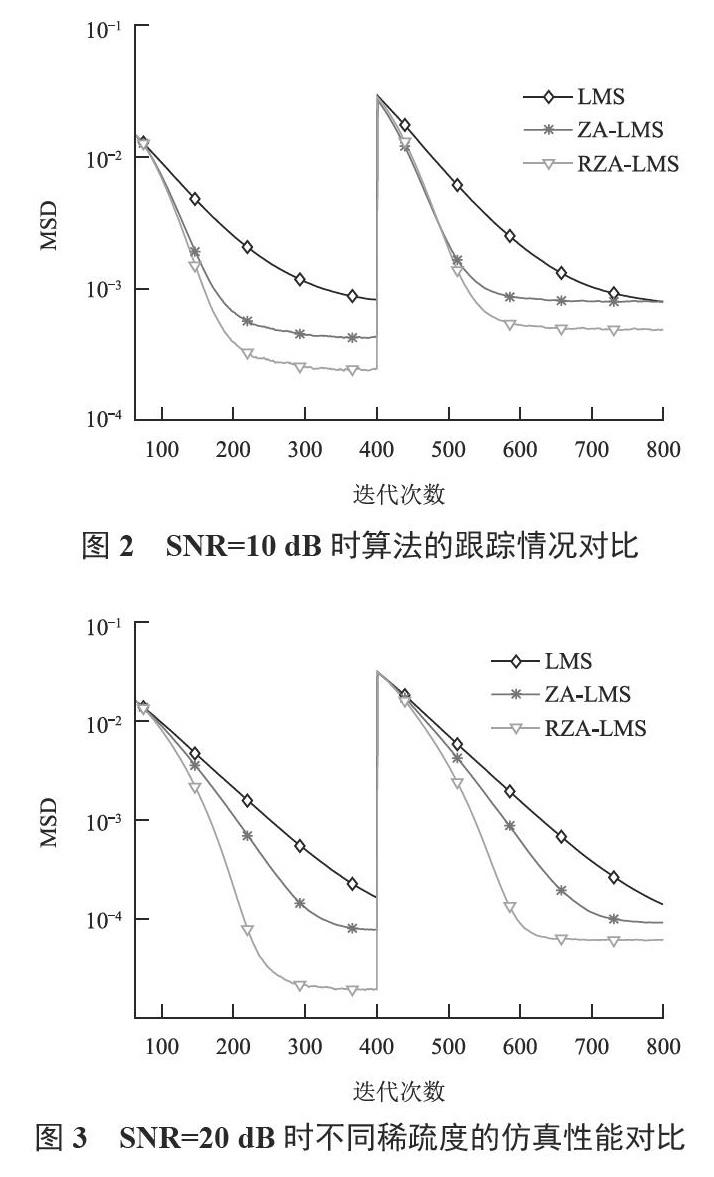
针对不同的信噪比环境进行2个仿真实验，目的是利用迭代方法评估不同参数下的信道估计性能。训练信号的长度均设为800，稀疏信道矢量h1和h2中非零系数的位置和大小均服从随机高斯分布，||h1||22=||h2||22=1，2个独立信道的长度均设置为32，故级联信道的长度为L1+L2-1=63，为了进行性能对比，同时对LMS算法和ZA-LMS算法进行仿真，信道估计参数与未知系统冲激响应抽头系数的平均偏差（Mean Squared Deviation，MSD）曲线变化情况如图2～图5所示。

实验1 测试不同信噪比下算法的收敛性能和跟踪情况。参数设置情况为：PS=1，PR=1，μ=0.01，ρRZA=3×10-4，ε'RZA=0.3，SNR=10 dB/20 dB。信道的初始稀疏度设置为1，迭代400次

后，信道冲激响应中非零系数的位置与大小皆发生跳变，信道的稀疏度变为4。算法独立运行100次，蒙特卡洛运行次数为1 000，信道估计的平均偏差曲线如图2、图3所示。

图2的信噪比环境为10 dB，图3的信噪比环境为20 dB。

由图2和图3可知，在算法迭代的初始阶段，3种算法的性能相距较近，RZA-LMS算法的收敛速度最快且稳态误差最小，ZA-LMS次之，LMS算法速度最慢、稳态误差最大。当信道状况发生改变，即系统的稀疏度由1变为4时，RZA-LMS和ZA-LMS算法很快能检测到系统的变化，并根据新的稀疏度进行信道估计。由仿真结果可知，系统的稀疏程度越高，稀疏度感知算法的估计性能越好，稳态误差就越小;稀疏程度降低，标准LMS算法的稳态误差仅有细微变化，稀疏LMS算法的稳态误差增大，估计性能虽有所降低但仍不低于标准LMS算法。实验1中各算法的稳态平均偏差数据见表1所列。

对比图2和图3，并结合表1中的数据可知，图2的数据对应表1中SNR=10 dB栏，20 dB栏对应于图3的稳态平均偏差。随着系统信噪比的提高，各算法的估计性能都有所改善，RZA-LMS算法的改善幅度最大。信噪比表达式SNR=10 log（PS/PN），在训练信号功率PS不变的情况下，当增加SNR时，噪声信号功率PN会随之减小，算法的估计性能得到改善，稳态误差降低。

实验2 加权零吸引算子ε'RZA的取值分析。本实验中的参数分别设置为：ε'RZA=0.3/0.1，SNR=10 dB，μ=0.012。当改变ε'RZA值时，RZA-LMS算法的估计性能随之改变，仿真结果如图4和图5所示，相应的稳态平均偏差数据见表2所列。其中，ε'RZA=0.3时的仿真结果对应于图4中各算法稳态偏差值，ε'RZA=0.1栏的数值是图5中各算法的稳态偏差值。

对比图4和图5曲线可知，ε'RZA=0.1时，RZA-LMS算法的信道估计性能较好，对于稀疏信道，加权零吸引算法能有效挖掘幅度接近于ε'RZA的抽头系数，将幅度小于ε'RZA的抽头系数趋于0。当ε'RZA取值很小时，该算子控制模型更接近于l0范数，当|hi（n）|>>ε'RZA时，收缩能力会减弱。因此，适当选取ε'RZA值将有助于减小RZA-LMS算法的稳态误差。

表2中的结果均大于表1中的数值，当增大梯度下降步长时，系统的收敛速度加快，系统误差能快速达到稳态，但稳态误差将增大;当减小梯度下降步长时，系统的稳态误差将降低，但系统的收敛速度变慢。

4 结 语

本文提出了基于稀疏度自适应的加权零吸引最小均方协同信道估计算法，该算法的复杂度较小。此类算法不涉及观测矩阵相应特性的验证问题，计算量得到了大幅减小，经过仿真，证明了算法的有效性，突破了系统稀疏度未知情况下压缩信道感知的局限性，验证了自适应压缩感知理论的可行性。

参考文献

[1] LANEMAN J N，TSE D N C，WORNELL G W. Cooperative diversity in wireless networks： efficient protocols and outage behavior [J]. IEEE transactions on information theory，2004，50（12）：3062-3080.

[2] SEYFI M，MUHAIDAT S，LIANG J. Capacity of selection cooperation with channel estimation errors[C]// Communications. IEEE Xplore，2010：361-364.

[3]张爱华，李春雷，桂冠.基于压缩感知的协同OFDM稀疏信道估计方法[J].计算机应用，2014，34（1）：13-17.

[4] GAO Z，DAI L，HAN S，et al. Compressive sensing techniques for next-generation wireless communications [J]. IEEE wireless communications，2018，25（3）：144-153.

[5] HU C，DAI L，MIR T，et al.Super-resolution channel estimation for mmwave massive MIMO with hybrid precoding [J]. IEEE transactions on vehicular technology，2018，67（9）：8954-8958.

[6]李子高，李淑秋，闻疏琳.一种改进的正交匹配追踪的DOA估计方法[J].测控技术，2017（1）：27-31.

[7]张凯，薛伦生，陈西宏，等.基于压缩感知的OQAM/OFDM系统POP方法信道估计[J].测控技术，2017，36（12）：33-38.

[8] TROPP J A，GILBERT A C. Signal recovery from random measurements via orthogonal matching pursuit [J]. IEEE transactions on information theory，2007，53（12）：4655-4666.

[9] NEEDELL D，TROPP J A. CoSaMP：iterative signal recovery from incomplete and inaccurate samples [J]. Communications of the ACM，2009，26（3）：301-321.

[10] DO T T，GAN L，NGUYEN N，et al. Sparsity Adaptive Matching Pursuit Algorithm for Practical Compressed Sensing[C]// 2008 42nd Asilomar Conference on Signals，Systems and Computers，Pacific Grove，CA，2008：581-587.

[11] EMMANUEL J CAND?S，WAKIN M B，BOYD S P. Enhancing sparsity by reweighted l1 minimization [J]. Journal of fourier analysis and applications，2008，14（5）：877-905.

[12] HONG X，GAO J，CHEN S. Zero-attracting recursive least squares algorithms [J]. IEEE transactions on vehicular technology，2017，66（1）：213-221.

[13] SELESNICK I. Sparse regularization via convex analysis [J]. IEEE transactions on signal processing，2017，65（17）：4481-4494.

[14] SHEN X，GU Y. Nonconvex sparse logistic regression with weakly convex regularization [J]. IEEE transaction on signal processing，2018，66（12）：3199-3211.

[15] GRAY R M. Toeplitz and circulant matrices：a review [J]. Communication and information theoy，2006，2（3）：155-239.

[16] CHEN Y，GU Y，HERO A O，et al. Sparse LMS for system identification[C]// IEEE International Conference on Acoustics，Speech and Signal Processing，Taipei，2009： 3125-3128.

[17] GAO F，JIANG B，GAO X，et al. Superimposed training based channel estimation for OFDM modulated amplify-and-forward relay networks [J]. IEEE transactions on communications，2011，59（7）：2029-2039.

作者簡介：张爱华（1976—），女，河南濮阳人，副教授，博士，主要研究方向为宽带无线通信系统中的稀疏信道估计、通信信号处理、大规模MIMO。