半潜式浮式风机平台绕流力学特性与尾流分析
邓露 刘建祥


摘 要:柱体绕流是海洋工程领域的重要问题. 流体绕经海洋平台所产生的周期性涡脱会造成平台往复运动,这将加剧平台系泊结构疲劳损伤,降低结构疲劳寿命. 为研究多柱式浮式风机平台绕流的力学特性,厘清尾流之间的干扰机理,采用Delayed Detached Eddy Simulation(DDES)方法分析了半潜式浮式风机平台在不同来流角和流速下的力学特性,从相干结构层面研究了尾流干扰机理,并分析了立柱尾流之间的空间相关性. 结果表明:下游立柱的阻力系数平均值随流速变化而有较大波动;流场相干结构以流向涡和发夹涡为主;相干结构之间的相互作用是导致尾流干扰的原因;上下游立柱尾流具有不同的相干结构,但两者仍有较强的空间相关性. 研究结果可为深入理解多柱式海洋平台绕流现象提供理论参考.
关键词:半潜式平台;多柱绕流;相干结构;尾流干扰;空间相关性
中图分类号:O351.2 文献标志码:A
Abstract:Flow past cylinders is an important issue in ocean engineering. Periodical vortex shedding occurring around the offshore platform in current leads to reciprocating motion of the offshore platform, which may aggravate the fatigue damage and thus cause the reduction of fatigue life of the moorings. In order to study the mechanical characteristics of flow past multi-column floating wind turbine platform and understand the mechanism of wake interference clearly, numerical simulations were performed using Delayed Detached Eddy Simulation (DDES). The effects of headings and current velocities on the mechanical characteristics of the semi-submersible floating wind turbine platform were investigated. The mechanism of wake interference was studied from the level of coherent structures, and spatial correlation between different wakes behind the columns was also investigated. The results demonstrate that: (1) the average drag force coefficient of downstream column has a large fluctuation with the change of current velocity; and streamwise vortex and hairpin vortex are the main coherent structures; (2) the interaction between coherent structures results in wake interference; (3) the upstream wake and the downstream wake have strong spatial correlation, but their coherent structures are different. The research results provide a theoretical reference for understanding the phenomenon of flow past multi-column offshore platform.
Key words:semi-submersible platform;flow past multiple cylinders;coherent structure;wake interference;spatial correlation
日益增長的能源需求促进了海上风电行业的发展,半潜式浮式风机平台适用水深范围广,是一种开发具有储量丰富、风速大等优点的深水风能资源的重要海洋平台[1]. 长期以来,柱体绕流一直是海洋工程领域的重点问题[2]. 流体流经浮式风机平台的柱体结构时,柱体后方周期性脱落的漩涡会导致平台大幅往复运动,这将加剧平台系泊结构的疲劳损伤,甚至导致系泊结构疲劳破坏[3]. 因此开展半潜式浮式风机平台绕流研究有着重要的工程意义.
在单柱绕流方面,国内外学者针对单柱绕流的力学特性、流场特性及其影响因素等已进行了大量的研究,并取得了丰硕的成果[4-7]. 在双柱和多柱式结构绕流方面,贾晓荷和刘桦[8]采用大涡模拟方法分析了并列或串列排布的双圆柱的绕流特性,结果表明串列排布时,上游圆柱对下游圆柱受力有影响,并列排布时,两柱的阻力系数均值基本相等. 郑宇华和顾杰[9]的研究表明,间距比(双柱中心的间距与柱宽的比值)影响并列双柱开缝下方的漩涡个数、形态等. Kitagawa T和Ohtab H[10]采用大涡方法模拟了串列双圆柱的绕流特性,结果表明当间距比小于某一临界值时,只有下游圆柱有涡脱现象. 李聪洲等[11]研究了串列双柱绕流的力学特性,结果表明存在一个临界间距比使得圆柱的升力和阻力发生跳跃性变化. 刘为民等[12]的研究表明,0°和45°来流时,阵列四立柱柱群中立柱的涡脱频率大于单柱的涡脱频率,涡脱模式表现为2S模式. 刘正浩等[13]的研究表明,来流角对阵列四柱式海洋平台的立柱的升力和阻力系数影响较大,不同来流角下平台底部的流场不同.
双柱和多柱式结构绕流时,柱体尾流之间的相互干扰会导致立柱的力学特性和流场结构更复杂[11]. 然而,以上针对双柱和多柱式结构绕流的研究,主要分析了流速、来流角和间距比等因素对结构的受力、流场形态和涡脱模式等的影响,而深入分析流场结构以及尾流之间干扰机理的研究极少. 因此,本文采用DDES方法对不同来流角和流速下多柱式半潜式浮式风机平台的绕流进行了三维数值模拟,分析了平台立柱的阻力系数平均值、升力系数频率等力学指标,从流场的相干结构层面研究了尾流的干扰机理,并分析了尾流的空间相关性. 研究结果阐释了多柱式结构绕流的尾流相互干扰机理,为深入理解多柱式结构绕流现象提供了理论依据.
1 数值建模
1.1 DDES方法
DDES方法是一种改进的RANS与LES相结合的方法,其在模拟流体分离流动时十分有效[16],已得到广泛的应用. 该方法具有多个优点,如不需要精细的网格也能得到较好的结果,适合复杂的结构等. 因此,本文采用该方法进行研究.
1.2 平台模型
选取美国国家可再生能源实验室设计的半潜式浮式风机平台作为分析对象,平台的立柱(包括边柱和中柱)、连杆和浮箱底座的结构布置如图1所示(图中括号内为构件编号). 平台的结构尺寸,吃水深度等设计参数详见文献[17].
1.3 计算域与网格划分
流场计算域及模型平面布置如图2所示. θ 为来流角,即中柱与边柱2的连线与x轴负向的夹角. 流域入口边界距离边柱2中心为10D,出口边界距离边柱2中心为25D,左右邊界距离中柱中心均为10D. D为边柱直径.
边界条件设定为:入口为速度入口,出口为出流边界,顶部为自由边界,其余边界为对称边界,平台表面采用无滑移固定壁面.
网格划分示意图如图3. 由于平台几何结构复杂,因此,将流场分成两种类型的网格进行划分,在平台附近区域采用四面体网格以适应复杂的几何结构,在其他区域采用六面体网格以加快计算速度. 为控制网格密度,将流域分成九个区域,在平台附近和尾流区划分密集网格,其他区域则划分较稀疏的网格. 根据张新曙等[18]的建议,经过验算,并综合考虑计算耗时成本,确定网格方案为:加密区(平台四周1.4D的区域)的网格大小为0.12D;尾流区的初始网格大小为0.25D,且随着尾流远离平台,网格逐渐稀疏.
1.4 计算设置
流域采用Ansys Fluent进行求解. 时间离散采用二阶隐式格式,空间离散采用二阶迎风格式,压力与速度耦合方程采用PISO方法(Pressure-Implicit with Splitting of Operators). 时间步长取0.05 s,每个时间步长内最大迭代次数为20,模拟时长为6 000 ~10 000 s,以保证获得稳定的结果. 数据处理时,选取最后约0.6倍模拟时长内较稳定的计算结果进行处理.
1.5 计算工况
本文选取3种典型来流角:θ = 0°、30°、60°. 根据中国南海的实际情况[19],选取12种来流速度:u = 0.32 m/s、0.42 m/s、0.53 m/s、0.63 m/s、0.74 m/s、0.85 m/s、0.95 m/s、1.06 m/s、1.16 m/s、1.27 m/s、1.37 m/s、1.48 m/s,来流方向沿x轴正向.
2 计算结果及分析
2.1 力学特性
2.1.1 阻力系数平均值
图4 ~ 图7分别为中柱、边柱1、边柱2、边柱3的阻力系数平均值随来流角和流速变化的关系图. 从这四幅图中可知,在0°来流下,中柱的阻力系数平均值随流速的变化而小幅波动,其余立柱的阻力系数平均值随流速的改变而基本不变. 在30°来流下,边柱2和边柱3的阻力系数平均值随流速的改变而基本不变,但中柱和边柱1的阻力系数平均值随流速的改变而变化较大,离散性较强. 这是因为流体流经上游立柱后发展成为湍流,湍流本身具有较强的随机波动性,所以,受上游尾流的影响,下游中柱和边柱1的阻力系数平均值随流速的变化而波动较大[12]. 在60°来流下,中柱、边柱2和边柱3的阻力系数平均值随流速的改变而基本不变,而边柱1的阻力系数平均值出现了跳跃波动的现象. 这也是因为边柱1处于下游位置,其阻力系数平均值受上游尾流的影响较大.
由图4可知,中柱的阻力系数平均值随来流角的增大而减小. 阻力是漩涡脱落引起的立柱前后表面的压力差和立柱表面的摩擦力共同作用所形成的. 随着来流角的改变,立柱和立柱、立柱和底座在垂直于来流方向的相对距离发生了改变. 由图2的平面布置图可知,在0°来流时,中柱后方尾流距离立柱和底座较远,下游柱体的阻挡作用小,上游中柱的尾流漩涡能够充分地发展,所以阻力系数最大. 在30°来流时,边柱1和底座1靠近中柱尾流,下游柱体的阻挡作用增大,下游中柱后方的漩涡脱落不能充分发展,故阻力系数减小. 在60°来流时,边柱1和底座1位于中柱的正后方,完全阻挡了中柱尾流漩涡的发展,故阻力系数最小. 由图5可知,边柱1的阻力系数平均值随来流角的增大呈现先减小后增大的趋势. 由图6和图7可知,边柱2和边柱3的阻力系数平均值均随来流角的增大而增大. 这些也均是因为随着来流角的改变,柱体之间在垂直于来流方向的相对距离发生了改变,柱体与柱体之间的相互影响所导致的.
2.1.2 升力系数时程曲线及频谱分析
限于篇幅,仅给出了θ = 0°、u = 1.06 m/s时各个立柱的升力系数时程曲线,如图8所示. 从图8中可以看出,边柱2、边柱3和中柱的升力系数时程变化表现出较好的谐波特性,而边柱1的升力系数变化波动较大. 边柱2和边柱3的升力系数变化相反,中柱的升力系数变化滞后于边柱2. 当边柱2的升力系数达到波峰时,中柱的升力系数稍有增大,且曲线变化趋势发生了改变. 以图8中t1-t2时间段为例,此时间段内中柱的升力系数未按图中粗划虚线趋势变化,而是按实线趋势变化. 这可能是因为中柱处于边柱2的尾流中,当上游边柱2的升力系数达到波峰时,其后方的漩涡脱落,随后撞击到中柱上,导致中柱的升力系数稍微增大而改变了曲线的变化趋势.
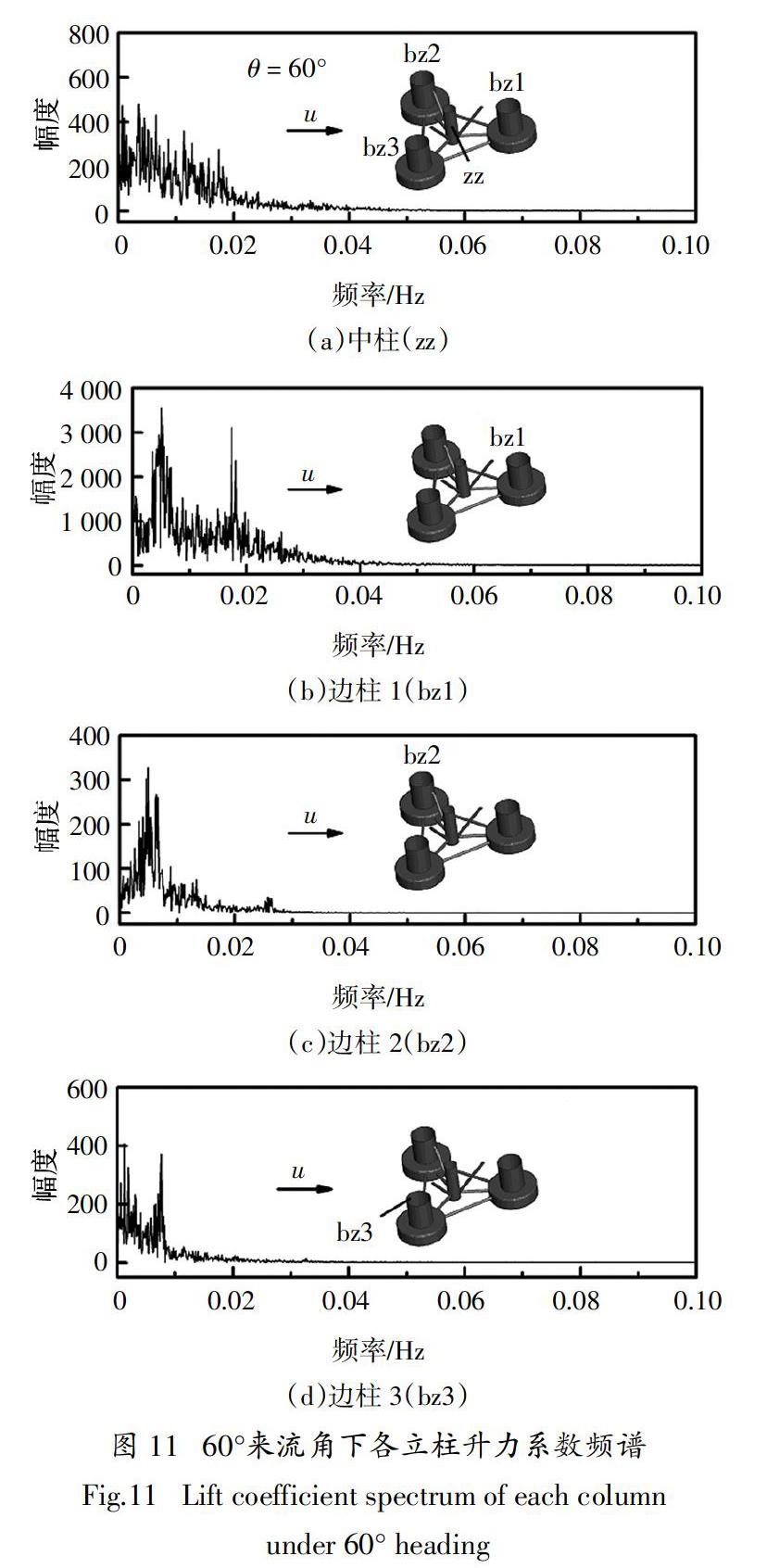
图9 ~ 图11为u = 1.06 m/s时,三种来流角下平台各立柱的升力系数频谱图. 立柱后方漩涡周期性地脱落是导致升力系数周期性变化的原因. 由图9可知,0°来流角下,中柱的频谱除主峰外,还存在多个高频的小峰,小峰的幅度远小于主峰的幅度,说明中柱后方漩涡脱落以主峰频率为主,并伴随多个高频成分. 边柱1的频谱图中存在两个较大的峰值,低频对应的幅度显著大于高频对应的幅度,说明边柱1后方低频的涡脱引起了较大的升力. 边柱2和边柱3的频谱图中均只有一个峰值,说明这两立柱后方的的漩涡为单频脱落. 此外,4个立柱的频谱图中均有一峰值对应的频率为f = 0.018 5 Hz. 综上可知,平台立柱后方漩涡脱落的主频率为f= 0.018 5 Hz,部分立柱还伴有高频或低频成分.
由图10可知,30°来流角下,中柱、边柱2和边柱3的升力系数频谱虽然有多个峰值,但对应的频率极低. 受上游尾流的干扰,下游边柱1的升力系数频谱没有明显的峰值. 可见在此来流角下,平台立柱后方漩涡脱落不规则.
由图11可知,60°来流角下,中柱频谱没有峰值,这是因为流体绕过中柱后,撞击在下游的底座1和边柱1上,没有形成周期性的涡脱. 其余立柱的频谱均有多个峰值,但没有相同频率的成分. 由此可见,平台立柱后方的漩涡呈多频脱落模式. 其他流速下,各柱的升力系数频谱也具有类似的性质,限于篇幅,不再赘述.
2.2 流场分析
2.2.1 流场相干结构与尾流干扰
湍流场中有组织性的漩涡结构称之为相干结构,其在湍流的发展演化中起着重要的作用[20-21]. u = 1.06 m/s时,0°、30°来流角下的涡量等值面图(按x方向速度u着色)分别如图12(a)、(b),涡量等值面采用Hunt等[22]建议的Q判据(Q-criterion)表示. 从图12中可以看出,流体流经平台后,形成了多种形式和尺度不一的漩涡. 图12(a)和(b)中的弧状涡包成月牙形分布在浮箱底座的底面和顶面边缘,反映出流体流经浮箱底座时,在底面和顶面边缘发生流动分离,并在随后的区域形成了马蹄涡. 图12(a)中,边柱1、边柱2和边柱3后方有成对的、错位排布的管状涡包,说明这些立柱后方形成了交替脱落、错位排布的尾涡,尾涡流经中柱后,逐渐拉长而发展成为流向涡. 从图12(b)中可以看出,边柱3后方形成了斜向下的锥形涡包,说明该处漩涡结构的半径随着水深的增加而逐渐缩小. 浮箱底座3后方呈螺旋状上升的螺旋涡包,反映出其后方形成了發夹涡[21],该漩涡结构由涡头和两条涡腿组成,涡头受到涡腿旋转向上的抬升力而上扬. 靠近浮箱底座的发夹涡的尺度明显小于远离底座的发夹涡的尺度,说明随着湍流的发展,发夹涡逐渐发展壮大.
流体流经平台时,平台的立柱、连杆和浮箱底座的尾流之间会相互干扰. 如图12(a)中所示,边柱2后方尺度较大的漩涡结构与下游斜杆2后方尺度较小的漩涡结构相互融合,最终汇合成为一个整体,相当于大漩涡“吞并”了小漩涡. 如图12(b)中所示,浮箱底座3后方形成的发夹涡在上扬的过程中,由于涡腿的旋转效应,诱导了边柱3的尾涡向斜下方运动,最终与浮箱底座3的尾涡汇合在一起,并导致了次生流向涡的形成. 此外,由于该发夹涡涡腿的旋转效应,也诱导了中柱后方的流向涡发生偏转弯折,从而改变了中柱尾流的流动方向. 由以上分析可知,尾流干扰的机理正是相干结构之间的相互作用.
2.2.2 空间相关性分析
流场内i、j两点的脉动量Xi、Xj在空间上的相关性可用相关系数R来表示,其定义[23]表示为:
当i = j时,表示该点的脉动量自相关,当i ≠ j时,表示两点的脉动量互相关. 相关系数的大小表征了脉动量在流场不同位置的关联程度,R = ±1表示完全相关,R = 0表示不相关.
图13为0°来流角下y = 0平面结构的剖面图. 为考察上下游立柱尾流间的空间相关性,选择x方向速度u作为脉动量,计算了y = 0平面,z = 1.17D高度处边柱2(bz2)尾流点与中柱(zz)尾流点的相关系数,计算结果如图14所示,其中,图14(b)为图14(a)的水平投影图.
由图14可知,边柱2尾流与中柱尾流的x方向速度在一定区间内具有较强的相关性. 经计算,x坐标在[0.85D,1.1D]区段的边柱2尾流与x坐标在[3.1D,3.4D]区段的中柱尾流的x方向速度的相关系数为0.4 < R < 0.55,表现出较强的正相关性,而x坐标在[1.7D,2D]区段的边柱2尾流与x坐标在[3.1D,3.4D]区段的中柱尾流的x方向速度的相关系数为-0.55 < R < -0.4,表现出较强的负相关性. 这说明虽然边柱2后方交替脱落的尾涡流经中柱后,变成了流向涡,但两立柱的尾流之间仍有着较强的空间相关性.
3 结 论
本文通过DDES方法研究了0°、30°和60°来流下半潜式浮式风机平台绕流的力学特性,并对平台的尾流进行了深入分析,得出以下结论:
1)由于尾流的干扰,下游立柱的阻力系数平均值随流速变化而波动,离散性大,而上游立柱的阻力系数平均值变化不大. 在0°来流时,平台立柱后方的漩涡脱落以某一主频率为主,并伴有其他高频或低频成分;60°来流时,平台立柱后方的漩涡脱落呈多频模式.
2)流场相干结构具有多尺度性,且类型多样,包括发夹涡、流向涡、次生流向涡、马蹄涡等. 相干结构之间的相互作用是尾流干扰的内在原因. 尾流干扰存在两种模式:处于上下游位置的立柱与连杆之间的尾涡相互交融,导致它们的尾流成为一个整体;浮箱后的发夹涡诱导立柱漩涡改变运动方向,导致立柱尾流汇入浮箱尾流或者运动发生偏转.
3)流体流经成串列排布的立柱时,即使流场的相干结构发生了转变,上下游立柱尾流之间仍有着较强的空间相关性.
参考文献
[1] 邓露,黄民希,肖志颖,等. 考虑气动阻尼的浮式风机频域响应分析[J]. 湖南大学学报(自然科学版),2017,44(1):1—8.
DENG L,HUANG M X,XIAO Z Y,et al. Analysis on frequency response of floating wind turbine considering the influence of aerodynamic damping[J]. Journal of Hunan University(Natural Sciences),2017,44(1):1—8. (In Chinese)
[2] 周强,廖海黎,曹曙阳. 高雷诺数下方柱绕流特性的数值模拟[J]. 西南交通大学学报,2018,53(3):533—539.
ZHOU Q,LIAO H L,CAO S Y. Numerical study of flow characteristics around square cylinder at high reynolds number[J]. Journal of Southwest Jiaotong University,2018,53(3):533—539. (In Chinese)
[3] DUAN F,HU Z Q,WANG J. Investigation of the VIMs of a spar-type FOWT using a model test method[J]. Journal of Renewable and Sustainable Energy,2016,8(6):063301.
[4] KUMAR A,CHANG H S,GOWDA L,et al. Influence of comer radius on the near wake structure of a transversely oscillating square cylinder[J]. Journal of Mechanical Science and Technology,2009,23(9):2390—2416.
[5] ZHANG W,SAMTANEY R. Low-Re flow past an isolated cylinder with rounded corners[J]. Computers and Fluids,2016,136:384—401.
[6] 端木玉,萬德成. 雷诺数为3900时三维圆柱绕流的大涡模拟[J]. 海洋工程,2016,34(6):11—20.
DUAN M Y,WAN D C. Large-eddy simulation of the flow past a cylinder with Re=3900[J]. The Ocean Engineering,2016,34(6):11—20. (In Chinese)
[7] 槐文信,柳梦阳,杨中华. 基于LES的圆柱尾流漩涡特性分析[J]. 华中科技大学学报(自然科学版),2018,46(5):95—99.
HUAI W X,LIU M Y,YANG Z H.Analysis of vortex characteristics in wake of circular cylinder based on LES[J]. Journal of Huazhou University of Science and Technology (Natural Science Edition),2018,46(5):95—99. (In Chinese)
[8] 贾晓荷,刘桦. 双圆柱绕流的大涡模拟[J]. 水动力学研究与进展A辑,2008(6):625—632.
JIA X H,LIU Y. Large eddy simulation of flow around two circular cylinders[J]. Chinese Journal of Hydrodynamics,2008(6):625—632. (In Chinese)
[9] 郑宇华,顾杰. 两并列矩形柱绕流的PIV试验研究[J]. 应用力学学报,2018,35(3):465—471+682.
ZHENG Y H,GU J. PIV experimental study on flow around two parallelized rectangular columns[J]. Chinese Journal of Applied Mechanics,2018,35(3):465—471+682. (In Chinese)
[10] KITAGAWA T,OHTAB H. Numerical investigation on flow around circular cylinders in tandem arrangement at a subcritical reynolds number[J]. Journal of Fluids Structure,2008,24(5):680—699.
[11] 李聪洲,张新曙,胡晓峰,等. 高雷诺数下多柱绕流特性研究[J]. 力学学报,2018,50(2):233—243.
LI C Z,ZHANG X S,HU X F,et al. The study of flow past multiple cylinders at high reynolds number[J]. Chinese Journal of Theoretical and Applied Mechanics,2018,50(2):233—243. (In Chinese)
[12] 刘为民,谷家扬,卢燕祥. 阵列四柱绕流的数值模拟[J]. 江苏科技大学学报(自然科学版),2012,26(6):534—540.
LIU W M,GU J Y,LU Y X. Study on the characteristics of flow around a four square cylinder array[J]. Journal of Jiangsu University of Science and Technology(Natural Science Edition),2012,26(6):534—540. (In Chinese)
[13] 劉正浩,赵伟文,万德成. 四柱式半潜平台绕流的三维数值模拟[C]//. 中国力学大会-2017暨庆祝中国力学学会成立60周年大会论文集(A). 北京:中国力学学会,2017:1—12.
LIU Z H,ZHAO W W,WAN D C. Numerical investigation of characteristics of flow past semi-submersible platform[C]//. Proceedings of the Chinese Congress of Theoretical and Applied Mechanics (CCTAM-2017) and the celebration of the 60th anniversary of Chinese Society of Theoretical and Applied Mechanics(A). Beijing:Chinese Society of Theoretical and Applied Mechanics,2017:1—12. (In Chinese)
[14] SPALART P R,JOU W H,STRELETS M,et al. Comments on the Feasibility of LES for wings,and on a hybrid RANS/LES approach[C]// Proceedings of First AFOSR International Conference on DNS/LES Approach. Ruston:Greyden Press,1997:137—147.
[15] SPALART P R,DECK S,SHUR M L,et al. A new version of detached-eddy simulation,resistant to ambiguous grid densities[J]. Theoretical Computational Fluid Dynamics,2006,20(30):181—195.
[16] 杜若凡,阎超,韩政,等. DDES延迟函数在超声速底部流动中的性能分析[J]. 北京航空航天大学学报,2017,43(8):1585—1593.
DU R F,YAN C,HAN Z,et al. Performance of delayed functions in DDES for supersonic base flow[J]. Journal of Beijing University of Aeronautics and Astronautics,2017,43(8):1585—1593. (In Chinese)
[17] ROBERTSON A,JONKMAN J,MASCIOLA M,et al. Definition of the semi-submersible floating system for phase II of OC4[R]. Golden:National Renewable Energy Laboratory,2014:1—38.
[18] 张新曙,胡晓峰,尤云祥,等. 深海多立柱浮式平台涡激运动特性研究[J]. 力学学报,2016,48(3):593—598.
ZHANG X S,HU X F,YOU Y X,et al. Investigation on the characterisitics of vortex induced motion of a deep sea muti-column floating platform[J]. Chinese Journal of Theoretical and Applied Mechanics,2016,48(3):593—598. (In Chinese)
[19] SHEIKH R,BROWN A. Extreme vertical deep water current profiles in the South China Sea,Offshore Borneo[C]// Proceedings of the 29th International Conference on Ocean,Offshore and Arctic Engineering. Shanghai:American Society of Mechanical Engineers,2010:585—595.
[20] PEREIRA F S,ECA L,VAZ G,et al. Challenges in Scale-Resolving Simulations of turbulent wake flows with coherent structures[J]. Journal of Computational Physics,2018,363:98—115.
[21] 陈槐. 封闭槽道紊流相干结构研究[D]. 北京:清华大学土木水利学院,2015:3—5.
CHEN H. Coherent structures in turbulent channel flows[D]. Beijing:School of Civil Engineering,Tsinghua University,2015:3—5. (In Chinese)
[22] HUNT J C R,WRAY A A,MOIN P. Eddies,streams and convergence zones in turbulent flows[C]// Proceedings of the 1988 Summer program:studying turbulence using numerical simulation databases,2. Palo Alto:Stanford University,1988:193—208.
[23] 胡昊,李新凯,戴丽萍,等. 涡发生器控制平板边界层分离的大涡模拟[J]. 航空动力学报,2016,31(2):493—502.
HU H,LI X K,DAI L P,et al. Vortex generators control flat boundary layer separation of large eddy simulation[J]. Journal of Aerospace Power,2016,31(2):493—502. (In Chinese)

