基于商业中心建设的位置优选算法研究

朱泽

摘 要：本文针对城市商业中心选址问题，以城市各区域到商业中心的交通成本作为评价指标，综合考虑各区域活动人口数量和交通建设水平等关键因素建立数学模型，基于欧式距离理论和层次聚类法，对部分算法进行优化和改进，提出了建立单个和多个商业中心的位置优选算法，通过迭代法进行数值求解，为同类型位置优选问题提供参考依据和指导建议。

关键词：位置优选 层次聚类分析 欧式距离 迭代算法

中图分类号：P208文献标识码：A文章编号：1003-9082（2020）06-0-02

引言

商业中心是一个城市商品流通的枢纽，承担着整个城市的商业职能，一个优良的商业中心，必须满足商业活动的基本要求：具有足够数量的消费群体，便利的交通，完备的功能[1]。因此要综合各项因素对商业中心进行位置优选，得到最佳选址。

一、建立数学模型

1.评价指标

对于商业中心而言，交通的便捷性是最重要的评价指标，商业中心每天履行承载大量商品运输交换职能以及大量人口快速流动的特性，所以对交通有严重依赖性[2]。因此，本研究将各个区域消费者到商业中心的交通成本作为评价指标，进行商业中心的位置优选。

2.影响因素

影响商业中心位置优选的因素有很多。不同区域的活动人口数量不同，活动人数越多，潜在消费概率越大;考虑到不同区域高速公路、公交、地铁等基础交通设施的建设情况，不同区域的交通建设水平也会影响各区域消费者到商业中心的交通成本和效率。因此，本研究综合考虑区域活动人数和交通条件两个重要因素，以T城市为例建立数学模型，探究位置优选算法。

本模型基本假设：各区域的活动人口集中为理想化质点;各个区域与商业中心距离均为直线距离。

3.参数前处理

T城市共有13个区域，各区域实际活动人口数量见表1;根据不同区域交通基础建设的完备情况，将其交通水平由低到高划分成A、B、C、D四个等级。

人口数量系数Pi为各区域的活动人口数量与城市活动人口总量之比，代表各区域活动人数的量级。

交通等级系数Ti表示不同等级的交通条件，基于模糊数学理论进行等级的量化处理，交通水平等级集为{很差，差，一般，好}，对应的数值为5，4，3，2，取偏大型柯西分布隶属函数[3]：

其中a，b，c，d为待定系数，且不同级别的隶属度满足：“很差”f（5）=1;“一般”f（3）=0.8，“很好”f（1）=0.01。解得a=1.1086，b=0.8942，c=0.3915，d=0.3699，将其代入上式可得f（2）=0.5245，f（4）=0.9126。

综上可得：TA=1，TB=0.9126，TC=0.8，TD=0.5245。各无量纲系数如下表所示：

表1 T城市各区域参数统计

区域名称 区域1 区域2 区域3 区域4 区域5 区域6 区域7

人口系数Pi 0.066 0.059 0.157 0.372 0.037 0.116 0.004

交通系数Ti 0.8 0.9126 1 1 0.8 1 0.5245

区域名称 区域8 区域9 区域10 区域11 区域12 区域13

人口参数Pi 0.029 0.019 0.053 0.024 0.007 0.012

交通等级Ti 0.8 0.8 0.9126 0.9126 0.5245 0.8

二、单个商业中心位置优选

1.标准化欧式距离

基于欧式距离理论进行各区域到商业中心的距离计算。表达式如下：

为综合考虑样本数据的归一性，采取改进和优化后的标准化欧式距离，将各个分量都标准化为均值和方差相等。样本集的标准化过程如下：

其中变量满足期望为0，方差为1。

2.位置优选算法

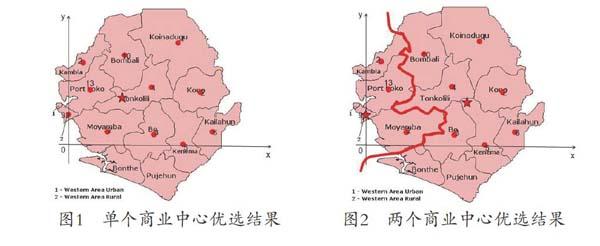
在T城市平面二维地图上选取坐标原点建立平面直角坐标系，如图1所示。将各个区域的理想化质点进行无量纲和标准化处理。

各个区域的理想质点标准化坐标为，商业中心的坐标为。综合考虑人口数量系数Pi、交通等级系数Ti，各个区域消费者到商业中心的交通总成本水平用Zall表示：

其中L表示交通单价比例系数，令

基于多元函数极值求解原理进行目标函数最小值求解，对xc和yc求偏导，并令其得零[4]，解得：

，

其中，dj未知，选择迭代法进行求解，在阈值范围内取作为初始坐标优选值，通过计算可得和第一次改善坐标优选值，

将改善坐标值作为初始值反复计算，直至，迭代结束，为最优解[5]。

按照上述方法进行计算，得到的T城市商业中心最佳建立坐标为，地处Tonkolili区内，如图1中五角星位置所示：

图1 单个商业中心优选结果     图2 两个商业中心优选结果

三、多个商业中心位置优选

当在T城市建立多个商业中心时，首先要根据距离属性进行区域聚类分析。

1.层次聚类分析

考虑本模型基本特征，研究采用自下而上的凝聚层次聚类法进行聚类划分：首先将每个区域坐标数据视为单个聚类，然后合并（聚合）成对的聚类，直到所有聚类合并成包含所有数据点的N个聚类，N即为最终目标聚类数量[6]。

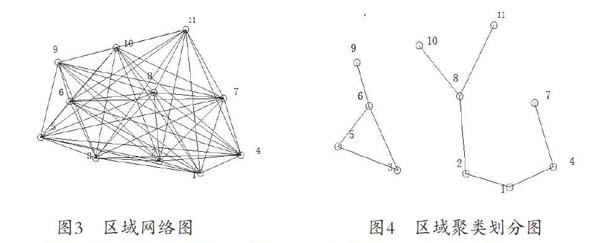
以建立两个商业中心为例，结合消费人群的实际情况，只考虑11个聚类，计算两两区域之间的最小距离，将距离最小的两个类合并成一个新类，重新计算新类与所有类的距离，重复操作直至所有类合并成两类。具体过程如下，首先以一定比例在坐标中绘制代表不同区域的点，将所有点两两相连，如图3所示，测量每两个区域之间的直线距离，整理成距离矩阵表。

图3 区域网络图图4 区域聚类划分图

将距离数据降序排列，按照先后顺序将距离最短的区域逐一合并，直到整个城市将被分为两个单独的区域，聚类停止，得到距离特性类似的聚类结果，如图4所示。

2.两个商业中心位置优选算法

对两个聚类地域进行商业中心优选位置，两个最优位置分别是、，得到各区域消费者到商业中心的交通总成本Zall。

同样利用迭代法在各聚类区域横纵坐标阈值内对和分别进行极小值求解，得到最优位置分别是Western区内的，和Kenema区内的，如图2中五角星标记所示。

结论

1.本文进行商业中心选址，充分考虑了人口因素和交通建设水平因素，并基于归一化和模糊数学理论将抽象因素量化处理，使得数学模型更加真实可靠;

2.本文进行单个和多个商業中心选址时，采用了优化后的标准化欧式距离公式，通过对数据进行标准化处理，可以提高计算的收敛性和准确性;

3.当进行多个商业中心选址时，要基于层次聚类理论进行聚类分析，依照自下而上的原理，以最小距离为聚类指标，进行递进聚类直至满足要求，然后在各自聚类区域内进行单一商业中心的位置优选。

参考文献

[1]李超.大型商场选址方案的模糊综合评价研究及应用[J].科技广场，2016，

（03）：143-146.

[2]刘斌，田晓雪.综合交通枢纽位置的优选[J].河南科技，2011，（20）：95.

[3]周克元，费绍金.高等教育学费标准的数学模型[J].佳木斯大学学报（自然科学版），2010，28（01）：120-122+128.

[4]孙娜.多元函数的极值问题及实际案例分析[J].数学学习与研究，2017，

（15）：31.

[5]朱夺宝.数学建模中迭代法教学探析[J].中国多媒体与网络教学学报（上旬刊），2020，（05）：239-241.

[6]林红阳，杜翼，刘林，易杨，蔡菁，马汉斌.基于动态层次K-Modes的电网数据聚类分析[J].四川电力技术，2019，42（06）：30-35.