树木生长方程的研究方法和研究过程

乔洪波

（山东省林业监测规划院，山东济南 250014）

为了全面提升森林质量，迅速扭转种质资源趋于退化的不良态势，从2010 年开始，数学经验方程在林业研究方面得到了广泛应用，胡海燕[1]、王亲波[2]等对树木成熟龄进行了系统研究；巩延苹[3]对树木生长量与降水量的关系进行了研究；张德全[4]对气候干湿周期进行了研究；矫兴杰[5]、张靖[6]、董兴囤[7]、杨科家[8]分别在碳储量、生长节律、光照影响与生长因素影响剔除等方面进行了研究。笔者经过长期研究发现，光照、降水、气温是影响树木生长的主要生态因子，但是其影响程度需要在时间尺度上进行表达。

笔者认为时间因素也应是影响树木生长的因子，只不过这一因子具有周期性、恒定性、均衡性、不可改变等特点，别的因子表现均要通过时间因子尺度上的表达，笔者在经验方程成长方程y=exp（a+bt）与阻力方程y=exp（a-b/t）（其中y 为树木的各种生长量指标，如树径、树高、材积等，为因变量，t 为影响因子时间值，a、b为待求系数，树木一般不会出现负增长，故b一般为正值）融合平衡精度中发现，对于完整龄阶（即树木年龄能被龄阶值完全整除，否则由于最后一个龄阶年龄数低于龄阶值，故称不完整龄阶），25 ～28 个样本为平衡试验精度最高的区间，而且波动较大，以28 样本为精度最高，而且试验精度是渐变的，笔者将300 年侧柏作为研究对象，因此采用12 a 为龄阶，其样本数为25 个，为完整龄阶，以期找到更为理想的研究结果，达到更高的研究精度。然后再分别用11 a、10 a 为龄阶进行研究，然后进行相互比较，以观试验效果如何。

1 资料来源

解析木材料为2013 年12 月采自山东省枣庄市山亭区山亭林场，是所有试验解析木中树龄最大的一棵。

2 研究方法

先用经验方程y1=exp（a1+b1t）和y2=exp（a2-b2/t）（为了区别，在函数和待求系数中加了下标）建立树木生长量与树木生长年龄的回归关系，求得待求系数a1、b1、a2、b2，在这里y1、y2为以时间t 为自变量、树木实际生长量（实测值）为因变量得到的经验方程拟合值。

如 果 令y3=exp（a3+b3t）和y4=exp（a4-b4/t），y3、y4为对y1、y2而言，将上述的树木生长量（实测值）替换为y1^m×y2^n，其中m、n为小于的纯小数，满足m+n=1的条件，并且使得方程y3、y4的方程拟合精度完全相等，m、n 用电子表格计算采用逐步接近的办法解决求算问题，笔者将求算精度定为1/109。经过大量验算得出以下结论：不分树种、立地条件的差异，不分树木生长指标性质的不同（如树径、树高、材积等），只要是起始年龄相同、时间因素对应的样本间隔一致或者是具有相同的倍数，再加上适当的系数调整，y3、y4的方程拟合精度完全相等，笔者把精度定义为平衡精度。

3 研究过程

3.1 12 a 龄阶侧柏生长过程原始拟合 以12 a 为龄阶，试验结果如表1 所示，与1 a 龄阶的试验结果相比，试验精度相对下降了0.49%，生长量翻番所需时间相对提高9.41%，也就是说增长势头下降了9.41%，因此样本减少使试验精度降低，研究结果可靠性也降低。同1 a 龄阶的试验结果相比，由于试验样本减少，而使试验精度稍有下降，但是2.5 m 以下树径与材积方程拟合结果与国家有关标准侧柏81 a 的成熟龄标准更为接近，相对误差只有20.62%，因此12 a 龄阶方程拟合结果更有现实意义（对于1 a 龄阶的试验结果而言）。

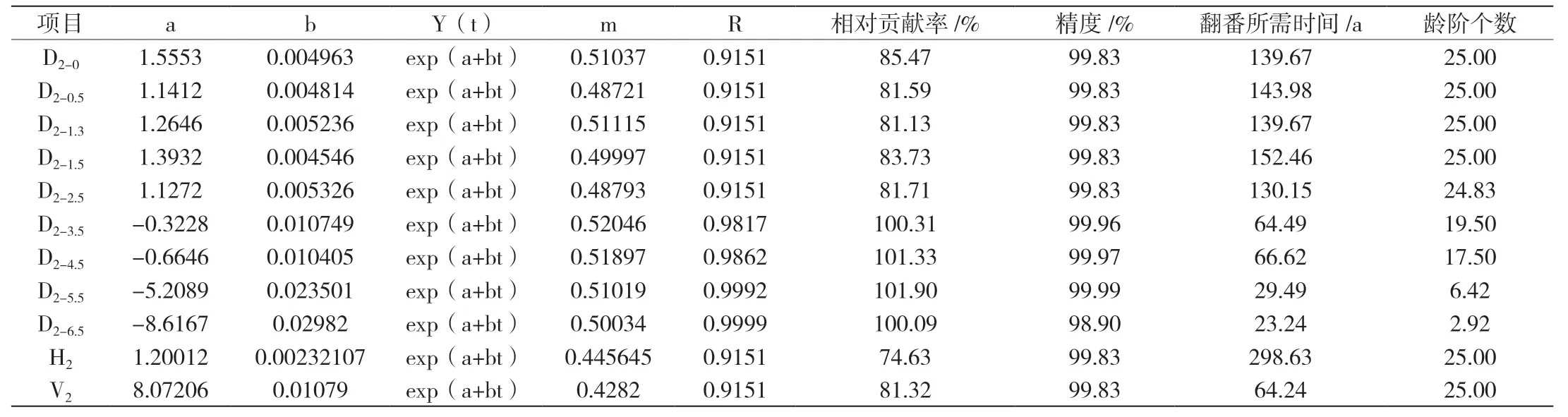
表1 300 a 生侧柏生长过程经验方程融合平衡状态表

3.2 12 a 龄阶生长过程经验方程融合 以12 a 为龄阶，同1 a 龄阶试验结果相比，m 值平均提高7.02%，说明试验结果反而使在平衡状态下树木上升作用同1a 龄阶试验结相比有所提升；相对贡献率平均提高18.19%，说明为了克服阻力作用，树木上升作用具有更大的贡献；平均试验精度下降0.99%，主要是试验样本数减少造成的，如果剔除样本极少的D2-6.5项目其平均精度反而上升0.02%，因此试验精度变化不大；平均翻番时间下降了21.06%，说明上升作用在明显增强。平衡状态同1a 龄阶试验结相比，试验精度的表现及m 值与3.1 完全一样，不再累述；虽然b 值平均下降16.77%，但是D2-0、D2-0.5、D2-1.3、D2-1.5、D2-2.5平 均 值25.54 的2 倍 为51.08 a，离国家成熟龄标准80 a 只差36.15%，比1 a 龄阶试验结果更为接近现实，说明树木的生长有趋向平衡状态的态势。树高项目提高6.05 倍，材积项目提高4.27 倍，材积项目55.38的数值与国家成熟龄标准只差30.78%了，更为接近了，D2-3.5、D2-4.5、D2-5.5项目同1 a 龄阶试验结果差别不大，说明表现比较稳定，差别最大的是D2-6.5项目，下降33.18%，说明树高表现越不稳定，试验结果同1 a 龄阶试验结果更加符合实际情况，就是说一些偶然误差在龄阶内得到了消化。

3.3 12 a 龄阶生长过程经验方程融合的平衡对比试验 试验表明，大于3.5 m 树径项目试验精度已明显低于95%，故不再列出，即认为树木的上升作用被完全排除，即二者具有相似的作用，说明试验比较成功。3.5 m 径、4.5 m 径、5.5 m 径、6.5 m径的试验精度分别为86.34%、84.10%、75.19%、0.00%，随着高度增加依次降低，说明本试验随着高度增加更有其现实意义。其余项目由于样本数目一样，试验精度保持一致，同1 a 龄阶试验结果的99.52%相比，下降4.28%；成长作用相对贡献率也差别不大，平均为15.93%，比 现实状态成长方程的26.51%相比下降39.91%，说明随着样本的减少方程的剔除作用增强。对于阻力方程的表现，试验精度与成长方程表现完全一致，但是由于b 值均为负值，已失去实际意义，说明其阻力作用已被剔除，笔者不再列出。但是比照上文的做法，取其商的倒数，即分子分母互换，试验精度不变，阻力方程的b 值就为正值了。

同1 a 龄阶试验结果相比，平均实验精度提高0.2%，变化不大。D2-1.3项目的b 值的二倍为54.26，与V2项目的b值54.85 相比相差1.08%，而与1 a 龄阶试验结果没有这样的表现，而是大相径庭，从另一个侧面说明该试验较为准确（根据测树学理论，材积与胸径的平方呈正比关系）。

4 讨论

以12 a 为龄阶比1 a 为径阶的样本数量减少，但试验精度及试验的现实性有所提高，不言而喻，龄阶的时间增长，无疑能够减少年轮判读的工作量，二者相比能减少91.67%，其试验的现实性和可操作性都有所提高，至于以多大的年龄段作为最佳选择的龄阶，有待在以后的试验中加以解决。由于时间仓促和水平有限，不足之处在所难免，诚望有识之士多提宝贵意见。