一类解三角形问题的多角度思考

杨苍洲

(福建省泉州第五中学 362000)

一、典例分析

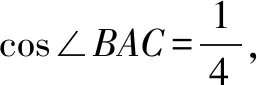
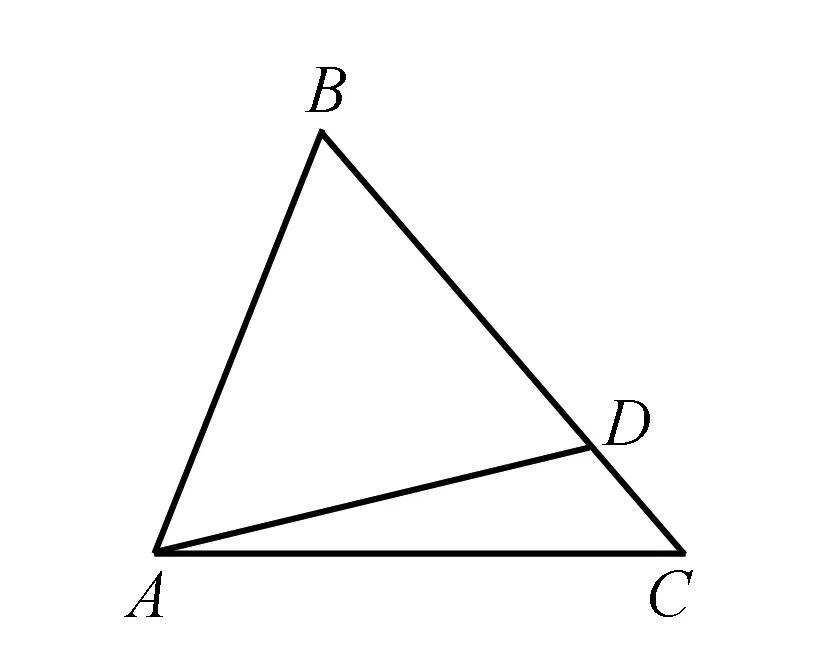
图1

解析设BC=a，AC=b，AB=c.

方法一向量法

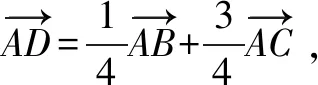
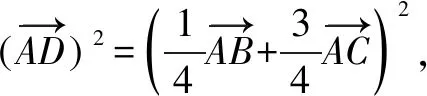
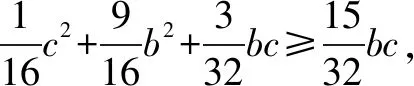
因此△ABC的面积

方法二算两次的方程思想

在△ABC中，

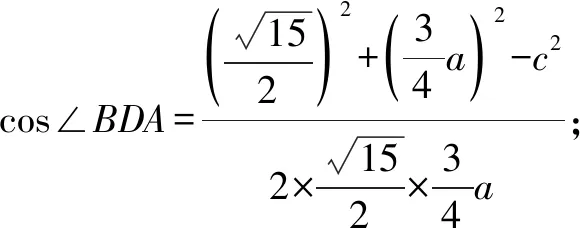
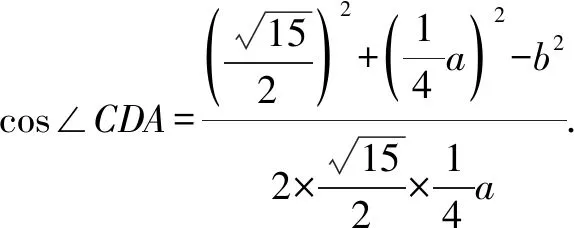
因为cos∠BDA=-cos∠CDA，

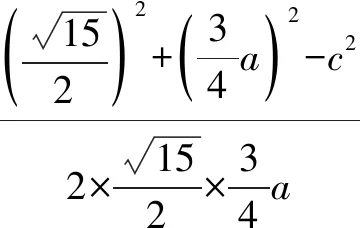
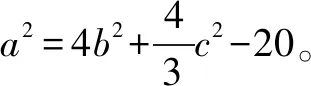
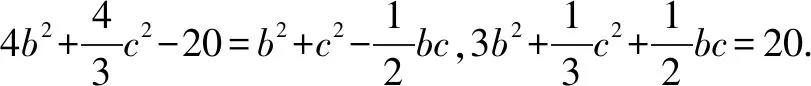
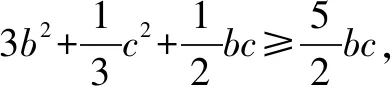
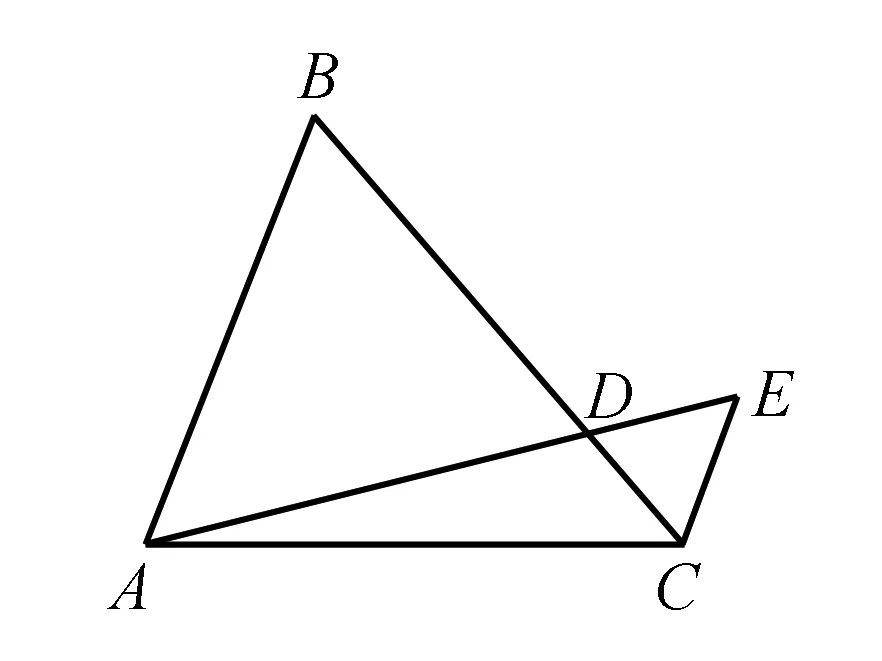
图2

因此△ABC的面积

方法三结合平面几何的转化法

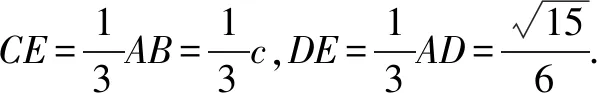
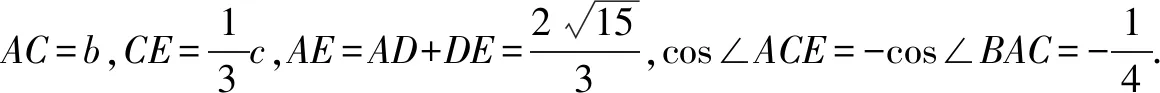
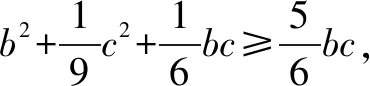
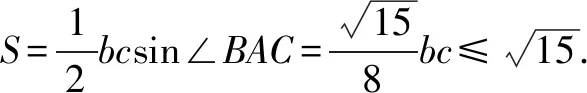
方法四结合平面几何的转化法

在AC上取点E使得DE∥AB.

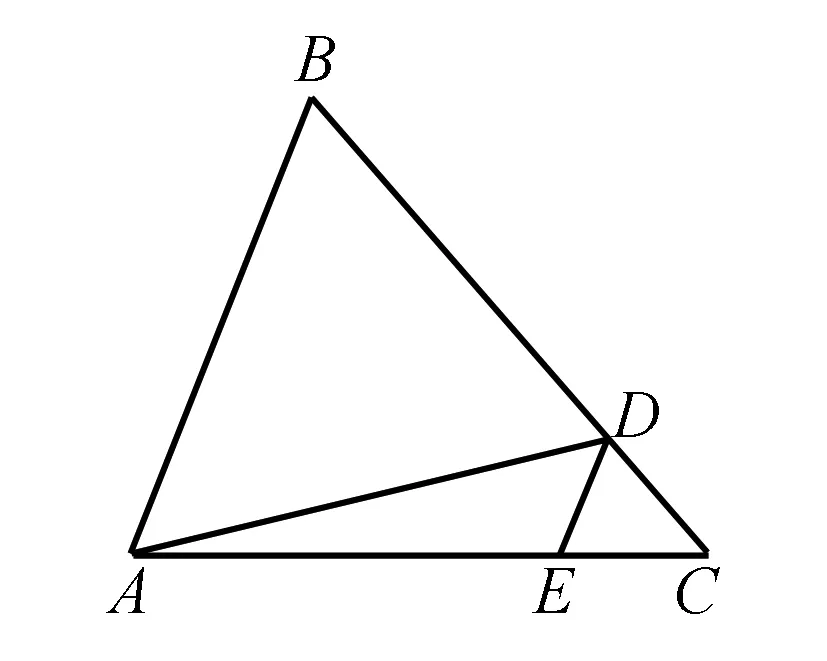
图3

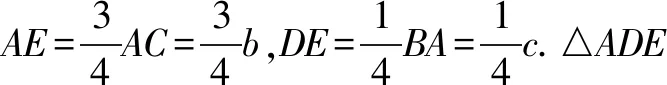
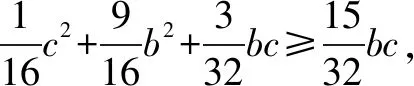
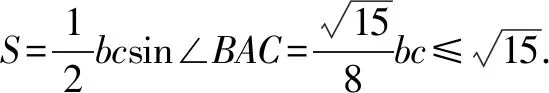
二、解法探究

1.试题结构识别

2.解题方法探究

思路二分别在△ABC，△ABD，△ACD中解三角形，注意到AD分别在△ACD、△ABD三角形内，∠BDA与∠CDA互补，BC=BD+DC等，应用算两次的方程思想，从而可得a,b,c,∠BAC的关系，再根据具体问题进行转化；

思路三结合平面几何进行转化，先构造平行线，从而得到相似三角形，得到对应边成比例，再把已知的量集中在某个三角形内，解三角形得到a,b,c的关系，再根据具体问题进行转化.

三、类题赏析

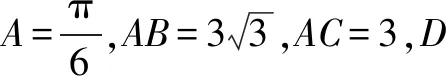
答案：D.

2．在△ABC中，AB=AC，D为AC的中点，且BD=1，则△ABC周长的最大值为( ).

答案：D.

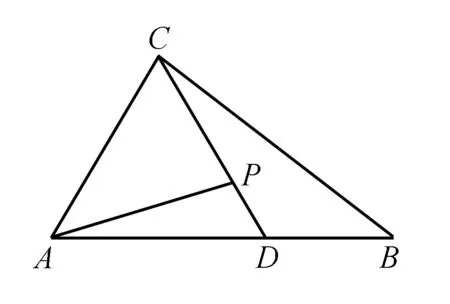
图4

答案：B