出奇制胜 巧妙构造

关传平

(河南省濮阳市第一高级中学 457000)

构造法应用的技巧是“定目标构造”，需要从已知条件入手，紧扣要解决的问题，把陌生问题转化为熟悉问题，包括构造函数、构造方程、构造图形、构造数列等.

一、构造函数

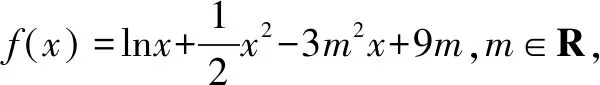
解析因为在区间[e,+)上，对任意的x1和x2，当x1>x2≥e时，都有成立，化简得f(x1)-f(x2)>x1-x2，即f(x1)-x1>f(x2)-x2恒成立.设则p(x)在[e,+)上单调递增，所以在[e,+)上恒成立，即恒成立，所以令因为在[e,+)上恒成立，所以在[e,+)上单调递增，x=e时取最小值，即所以解得：

反思解题时利用不等式的性质，通过“f(x1)-x1>f(x2)-x2”，构造出函数“p(x)=f(x)-x”，通过研究函数p(x)的单调性，求出了m的范围，解题的关键是抓住了式子的结构特征，构造了对应的函数.

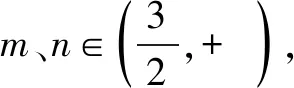
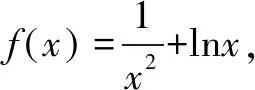
二、构造方程

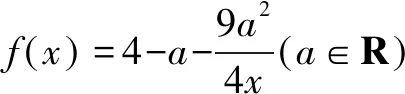
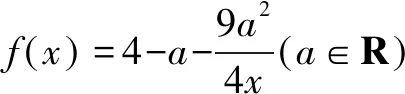
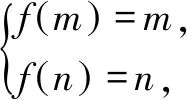
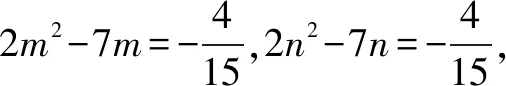
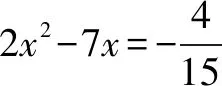
三、构造图形

例3已知球O的直径为10cm，线段AB、CD是球O的两条弦，且AB=CD=5cm，试求V三棱锥A-BCD的最大值.

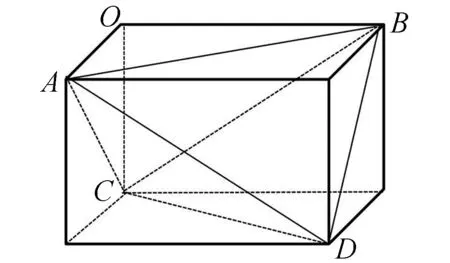
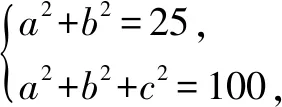
反思本题通过构造图形，把三棱锥体积的最大值转化为求长方体体积的最大值，使问题简单化.处理问题时，应把陌生的转化为熟悉的，把复杂的转化为简单的，把不够直观的转化为直观易懂的.

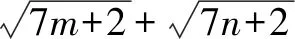
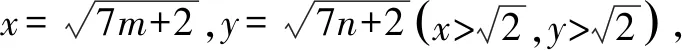
四、构造数列

例4已知数列{an}满足an-3an-1=n+6(n≥2)，a1=2，求{an}的通项公式.

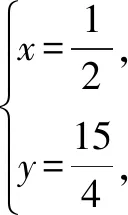
反思本题通过构造新的等比数列，使问题柳暗花明，迎刃而解.在数列中，遇到形如an=pan-1+q(p、q是常数)、an=pan-1+f(n)的递推式，一般使用构造等比数列的方法.

练习已知数列{an}满足an=2an-1+3n(n≥2)，a1=6，求{an}的通项公式.

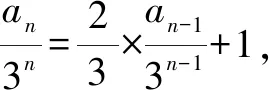
构造法适用于各种题型，我们在构造的时候，关键是抓住式子的特征，从而找到合适的对象去构造，做到精学一题、妙解一类，归类建档、内化于心.茫茫题海，寻根悟法方是岸！