选择适当数学模型 提升数学运算能力

陈海珍

(福建省宁德市古田县第六中学 352200)

数学运算作为《普通高中数学课程标准(2017年版)》一文在“课程基本理念”中创新性提炼出的六大核心素养之一.数学运算能力能够比较准确地反映出一名学生的综合能力，也直接影响着学生的考试水平.正确掌握与探究数学运算的原理以及破解问题的实践是有效提升数学运算能力的重要方面.合理选择适当的数学模型，将实际数学问题加以有效归类与转化，对提升学生的数学运算能力极有成效.

一、函数模型

例1(2019年高考数学全国卷Ⅲ理科第11题；文科第12题)设f(x)是定义域为R的偶函数，且在(0，+∞)单调递减，则( ).

分析选择满足题目条件的特殊函数模型，有针对性地分析与比较，从而得以确定抽象函数值的大小关系问题.

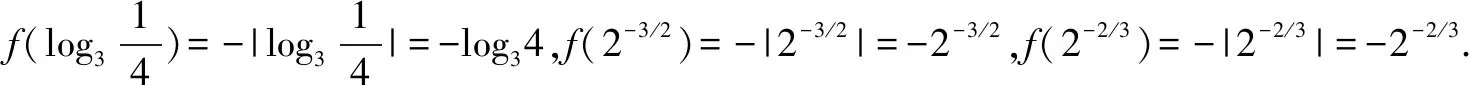
点评常见思维是利用抽象函数的性质来分析，比较繁琐.而通过选取满足条件信息的数学模型——特殊函数，可以快速准确地解答相关的函数问题，进而得以判断.解决此类问题的关键是根据题目条件选取简单的满足题目条件的数学模型——基本初等函数，熟练掌握基本初等函数的相关性质是利用特殊函数法解决问题的关键.

二、方程模型

分析引入相关的参数，通过构造对应的二次方程，结合方程有解的特征，利用判别式法来确定代数式的最值问题.

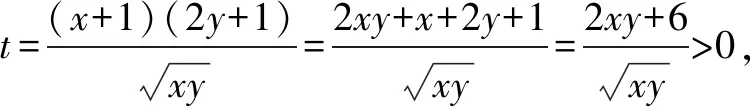
点评常见思维是利用借助基本不等式法来处理.而借助相应的方程模型的构造，引入参数，通过方程的转化，结合方程有解的前提条件，利用方程的判别式法加以转化与应用即可.构造方程模型对于破解最值、参数值的取值范围等相关的数学问题有奇效.

三、图形模型

例3(2019年高考数学北京卷理科第8题)数学中有许多形状优美、寓意美好的曲线，曲线C：x2+y2=1+|x|y就是其中之一(如图1)，给出下列三个结论：

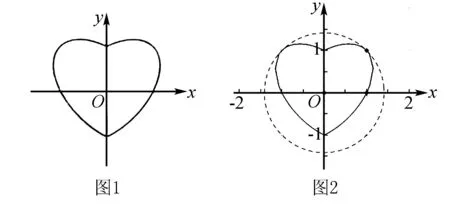
①曲线C恰好经过6个整点(即横、纵坐标均为整数的点)；

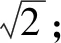
③曲线C所围成的“心形”区域的面积小于3.

其中，所有正确结论的序号是( ).

A.① B.② C.①② D.①②③

分析根据题目条件，选择网络图形，把“心形”图放在网格图中，借助网络图形的直观性加以分析与判断.

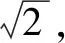
点评常见思维是利用逻辑推理法来分析与处理.而通过图形模型的建立，数形结合法处理，借助平面直角坐标系对应的网格图，可以直观快捷地解决问题，省时省力，减少数学运算与推理过程，解题效益高.

四、平面几何模型

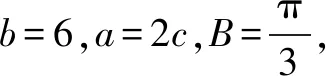
分析根据题目条件，合理选择与题目条件对应的直观平面几何模型——三角形，借助三角形的直观性，通过解平面几何来处理相应的解三角形问题.

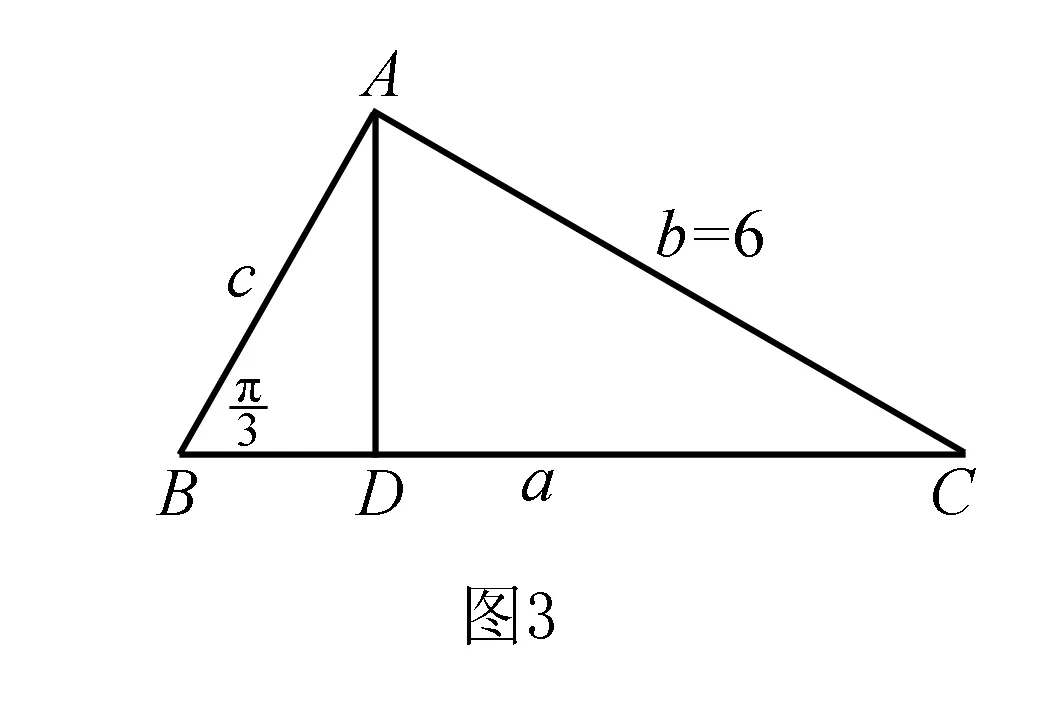
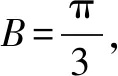
点评常见思维是借助余弦定理加以转化，进而确定边长c的值，再结合三角形的面积公式来处理.而这里借助平面几何图形的直观形象，利用直角三角形的性质与三角函数的定义来处理，巧妙通过勾股定理来确定边长c的值，处理起来直观有效，简化数学运算，破解起来也比较方便，简单易操作.

五、解析几何模型

分析根据题目中相关的三角关系式的特征，构造单位圆模型，借助直线与单位圆的关系，把三角函数问题转化为解析几何问题来处理.

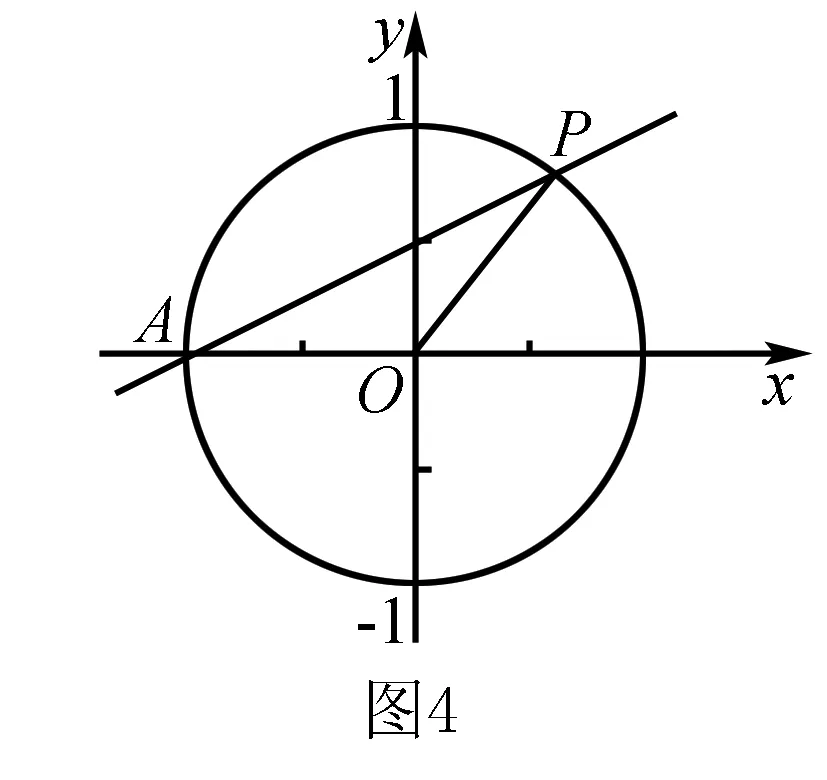
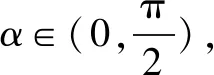
点评常见思维是利用三角函数公式合理切入，通过三角恒等变换公式以及同角三角函数基本关系式等加以处理，借助化归与转化思想，利用三角函数思维来进行分析与求解.而通过题目条件，巧妙借助解析几何中的单位圆的建立，通过直线与单位圆关系转化法来分析与处理，显得更为直观，破解起来更为方便，数学运算更为简单.

数学运算能力的培养与提高是一个贯穿学生整个数学学习的一条主要链条与脉络，教师应加强对学生数学运算能力的培养，有效提高学生学习数学的兴趣，借助不同数学运算方式的比较、感悟，不同数学模型的构造、选择，加深对相关数学概念与数学知识的理解与掌握，准确掌握运算规律，有效优化数学思维品质，提升数学能力，培养数学素养.