分类探索隐藏性相切关系下的题型

李昌成 黄晓玲

(1.新疆乌鲁木齐市第八中学 830002；2. 新疆生产建设兵团第一中学 830092)

直线与曲线，曲线与曲线相切在高中数学的解析几何和导数部分均有涉及，知识本身并不复杂，直接应用也比较容易.但是若把相切关系隐藏在题设中就会给学生在思维上造成很大的困难.研究发现，高考命题专家常常在这个点位上，考查学生的综合能力.因此，我们应当高度关注这个问题.下面分类探究，以飨读者.

一、在直线和曲线相切背景下的问题

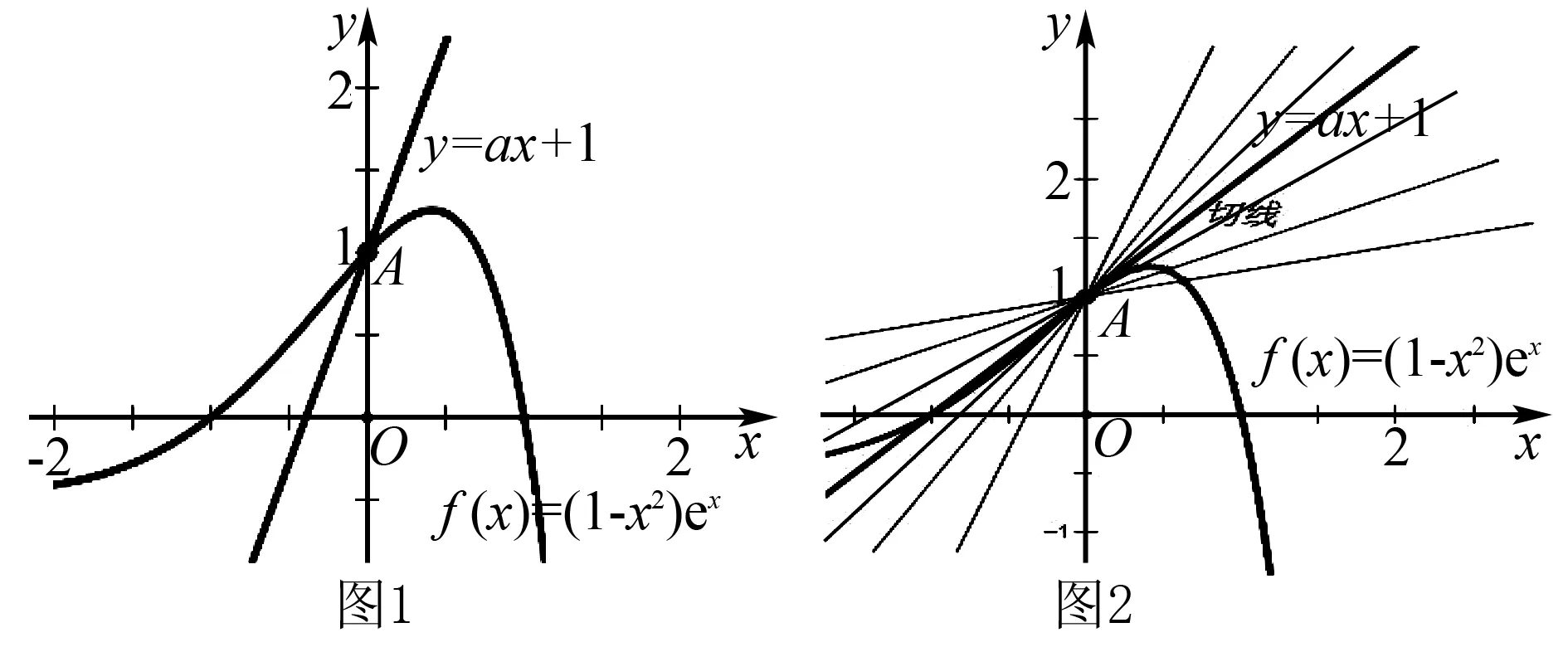
例1 (2017全国高考数学Ⅱ卷文科第21题第(Ⅱ)问)设函数f(x)=(1-x2)ex.当x≥0时，f(x)≤ax+1，求a的取值范围.

分析从几何意义看，要使x∈[0,+∞),f(x)≤ax+1成立，只需当x∈[0,+∞)时，射线y=ax+1始终在函数f(x)=(1-x2)ex图象的上方(仅在端点x=0处重合，如图1).进一步发现，直线y=ax+1位于曲线f(x)的切线位置是f(x)≤ax+1成立的极限情形：即若射线y=ax+1(x∈[0,+∞))位于切线位置或其上方时，均有f(x)≤ax+1；若射线y=ax+1(x∈[0,+∞))位于切线位置下方时，f(x)≤ax+1不恒成立(图2).

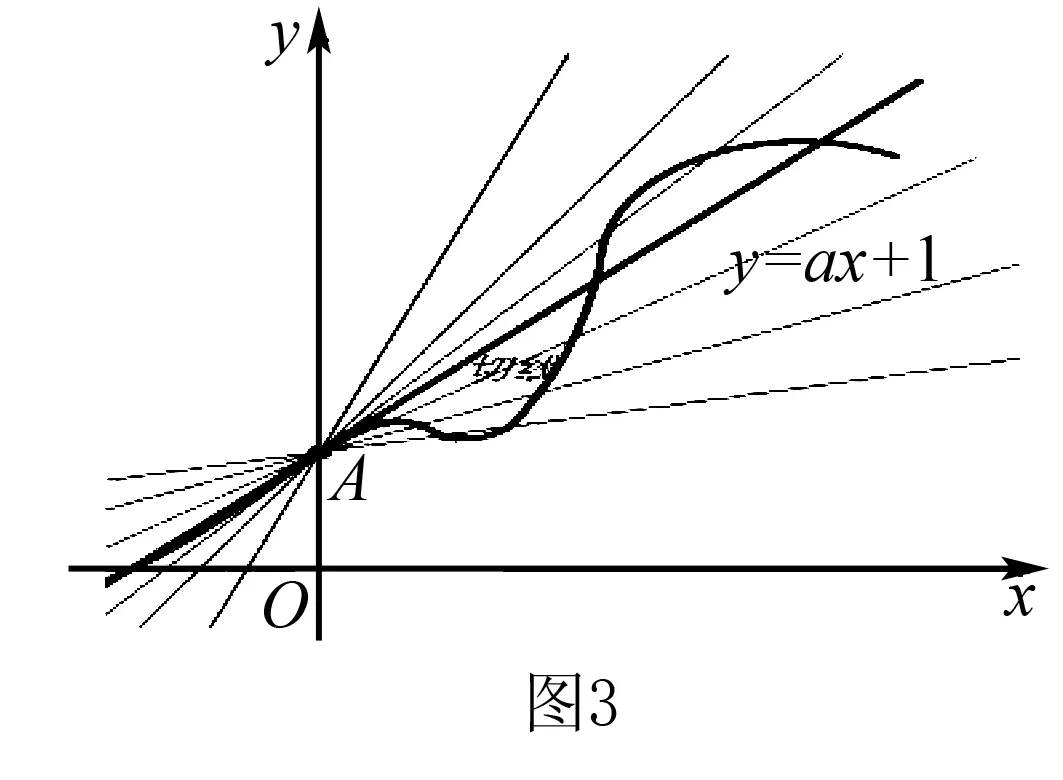
之所以如此，关键原因是f(x)=(1-x2)ex在x∈[0,+∞)上是凸函数(即曲线是上凸的).如若不然，则不能保证“当射线y=ax+1(x∈[0,+∞))位于切线位置或其上方时，均有f(x)≤ax+1”.例如图3中的反例.

解由f′(x)=(-x2-2x+1)ex知，曲线f(x)在点x=0处的切线方程为y=x+1.

当x∈[0，+)时，f(x)的图象始终位于其在点x=0处的切线y=x+1下方(仅在切点处重合).从而要使x∈[0，+)时，f(x)≤ax+1成立，当且仅当a≥1.

评注此题最常见的解法是分离参数构造函数，再利用导数求其最值，从而得解.但是一定会陷入“洛必达法则”的陷阱.本题的关键是切线意识，把握了切线这一实质，问题就迎刃而解.

(1)求椭圆E的方程；

(2)求∠F1AF2的角平分线所在直线l的方程；

(3)略.

评析本题不依托椭圆的切线就寸步难行，不知晓这个简便方法也会陷入繁杂纷扰的运算中，使用结论解答此题有效避开了直线和椭圆联立的二元二次大量运算，直接进入一元一次的运算，解答简捷明快.有兴趣者可以查阅高考参考答案，进行比较研究.

二、在曲线与曲线相切背景下的问题

例3 已知x，y∈R，且满足x2+2xy+2y2=6，则z=x2+4y2的取值范围为____.

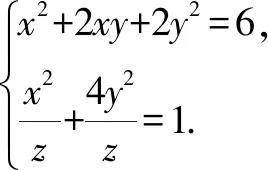
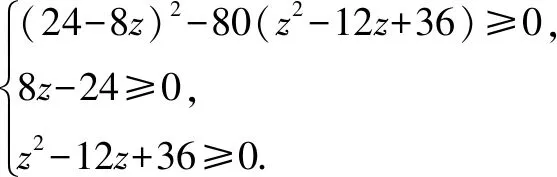
评注此题一般可以用三角换元、均值不等式等方法解答，但是因为系数做了一般化处理，以上两种方法均难以深入.利用二者之间的相切位置关系作答是一种通解通法.只因一些题目把题设特殊化，例如：已知x，y∈R，且满足x2+2xy+4y2=6，求z=x2+4y2的取值范围，利用三角换元、均值不等式等手段可以解答，但把问题的本质掩盖了.

三、在公切关系背景下的问题

例4 (2016年全国Ⅱ卷理科第16题) 若直线y=kx+b是曲线y=lnx+2的切线，也是曲线y=ln(x+1)的切线，则b=____.

分析切线问题是导数中最常见最简单的问题，但本题中公共切线把导数基础知识和整体代换技巧融为一体，把神秘的超越方程等价转化为可运算的简单方程，方程组思想使待定系数法能顺利实施.

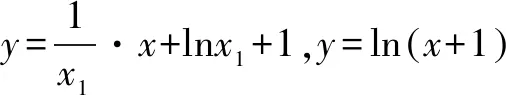
所以b=lnx1+1=1-ln2.

评注本题属于导数问题中最朴素的问题，但是公切线又赋予了问题新的内涵，难度猛然上升，融合了一些数学运算技巧，将抽象运算变得可操作，使题目档次上升，成为小题把关题.数学抽象、逻辑推理、数学运算、数据分析等核心素养融入其中.

在平时教学中，让学生从代数和几何的角度深刻理解相切的含义，能够提升学生的应用意识.尤其是两个角度的转化，往往是突破难题的关键.难题之所以难，就是因为学生思路受限或受阻，因此分门别类地研究相切关系，对学生能力的提高大有裨益.