拨开迷雾弄清性质 远离陷阱搞定函数

蒋 敏

(四川省南充龙门中学 637130)

函数是高中数学的重要内容之一，它引入了变量，在动态中探寻数学的秘密.然而，同学们在学习过程中往往会产生比较大的困难，比如思维上有漏洞，忽视一些基本原则，方法混乱瞎套用等，如何才能以不变应万变，妙解一题，精解一类？

一、定义域优先原则

对函数定义域的考查常常是通过函数性质或函数应用来考查的,且具有较强的隐蔽性.所以,在研究函数问题时必须树立起“定义域优先”的观点.许多同学就是因为忽视了函数定义域而导致解题错误.

例1已知函数f(x)=log3x+2,x∈[1,9]，求函数g(x)=[f(x)]2+f(x2)的值域.

令log3x=t,t∈[0,1]，则y=t2+6t+6在[0,1]上单调递增，所以值域为[6,13].

评注本题如果不思考g(x)的定义域，则缺少函数的三要素之一，从而导致值域错误.

例2已知奇函数f(x)是定义在(-3，3)上的减函数，求不等式f(x-3)+f(x2-3)<0的解集.

评注这个不等式问题本质还是函数问题，确定一个函数必须优先求出定义域，这样才能保证求解的范围不被放大.

二、单调性是函数的局部性质

函数的单调性也叫增减性，是刻画函数形态的一个重要性质.函数的单调性是对某个区间而言的,它是一个局部概念.

现象一：忽视分段函数在定义域分界点附近的单调性.

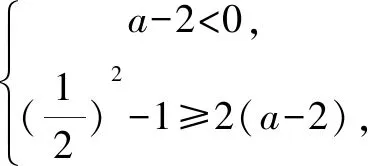
评注“分而不断”是分段函数的最重要特点，本题中函数除了在各段上单调递减外，还要保证整个函数在定义域内单调递减，求解中容易忽略函数在定义域分界点附近的单调性，从而错选A答案.

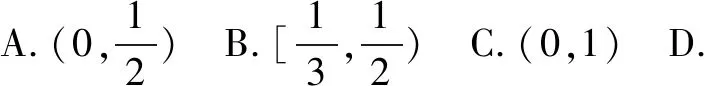
简解函数f(x)在R上为增函数，则：

现象二:混淆“在区间上单调”、“单调区间是”、“存在单调区间”等词意.

例4 函数y=-x2+2mx+5在[1,+∞)上为减函数，则实数m的取值范围是( ).

A.m≤1 B.m≥1 C.m≤-1 D.m≥-1

解析由函数y=-x2+2mx+5在[1,+∞)上为减函数，且该二次函数的对称轴为x=m，所以由数形结合知：m≤1，故选A答案.

评注本题容易错误理解为函数y=-x2+2mx+5的单调减区间是[1,+∞)，从而得出m=1的错误结论.在解题中要注意，“在区间上单调”指该区间是函数相应单调区间的子区间；“单调区间”是指该区间就是函数的相应最大单调区间；“存在单调区间”指该区间内有相应单调性，也可能有别的单调性，即该区间内可能既有增区间，也有减区间.

变式函数y=x2+2(1-t)x-8的单调增区间为[2,+)，则实数t的取值范围是____.

简解因为函数y=x2+2(1-t)x-8的单调增区间为[2,+)，所以t-1=2，即t=3.

三、奇偶性是函数的整体性质

现象一：在函数的奇偶性问题中错用或未关注“定义域关于原点对称”.

例5 已知函数f(x)的定义域为(3-2a,a+1)，且f(x+1)为偶函数，则实数a的值可以是( ).

解析函数f(x+1)的图象是由函数f(x)的图象向左平移1个单位得到，所以函数f(x+1)的定义域为(2-2a,a).又f(x+1)为偶函数，且偶函数定义域关于原点对称，则2-2a=-a，即a=2.故选择B选项.

评注若没有关注奇(偶)函数的定义域关于原点对称的性质，很可能错误地认为3-2a=-(a+1)，得到a=4，从而错选成选项C.

A.奇函数

B.偶函数

C.既是奇函数又是偶函数

D.既不是奇函数也不是偶函数

现象二：不能熟练应用“奇函数f(x)若在x=0处有定义，则f(0)=0”的结论.

例6 定义在R上的奇函数f(x)满足当x>0时，f(x)=2014x+log2014x，则在R上函数f(x)的零点个数为____.

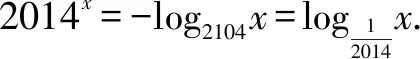
评注本题中若没有注意到“奇函数f(x)若在x=0处有定义，则f(0)=0”的结论，很容易得出在R上函数f(x)的零点个数为2的错误结论.

变式2 已知f(x)是定义在R上的奇函数，在区间(0,+)上单调递减，且则函数f(x)的零点个数为____.

现象三：复合函数奇偶性中错将含自变量的代数式当成自变量.

例7 函数f(x)的定义域为R，若f(x+1)与f(x-1)都是奇函数，则( ).

A.f(x)是偶函数 B.f(x)是奇函数

C.f(x)=f(x+2) D.f(x+3)是奇函数

在Leeway模型的基础上，首先基于内河流场的统计特征，建立风流影响下漂移速度预测模型，利用风流场数据的不确定性特征不断更新失踪物体的可能位置，然后结合航道岸线特征，预测失踪物体最终可能漂移终点位置的分布情况。

解析由f(x+1)与f(x-1)都是奇函数，可得：

则-f(x+2)=-f(x-2)，∴f(x)=f(x+4).故函数f(x)是以4为周期的周期函数.又由f(x-1)=-f(-x-1)得f(x-1+4)=-f(-x-1+4)，即f(x+3)=-f(-x+3)，∴函数f(x+3)是奇函数，选D.

变式已知函数y=f(2x+1)是偶函数，且f(2)=3，则f(0)=____.

解析∵函数y=f(2x+1)是偶函数，∴f(2x+1)=f(-2x+1)，故可得到f(x+1)=f(-x+1)，∴f(0)=f(2)=3.

现象四：分段函数奇偶性的分段处理上忽视“-x”的范围.

B.是偶函数

C.既是奇函数又是偶函数

D.既不是奇函数也不是偶函数

解析当x<-1时，-x>1，则f(-x)=-(-x)2+2=-(x2-2)=-f(x)；当|x|≤1时，

f(-x)=0=-f(x)；当x>1时，-x<-1，则f(-x)=(-x)2-2=-(-x2+2)=-f(x).

所以恒有f(-x)=-f(x)，即函数f(x)为奇函数，选A.

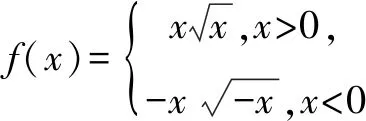
A.奇函数 B.偶函数

C.既是奇函数又是偶函数

D.既不是奇函数也不是偶函数