二次根式化简求值的解法和推广

洪 云 胡仁建

(1.福建省漳州市第三中学 363000；2. 重庆市潼南区康乐小学 402660)

二次根式的化简和运算是中学数学的重要内容之一,也是数学竞赛中的常见题型.二次根式的化简,除了掌握基本概念和运算法则外,应根据根式的具体结构特征,灵活选用一些特殊的方法和技巧，不仅可以化难为易、化繁为简,提高解题速度,收到事半功倍的效果,而且有助于培养分析问题、解决问题的能力及探索求新的学习习惯.以下就几类常用的方法和技巧举例说明.

一、拆裂项及因式分解

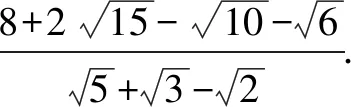
解析本题的关键是将分子中的8拆数配方因式分解，进而约分求得结果.

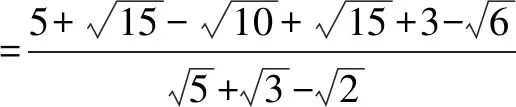
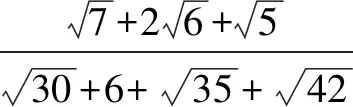
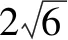
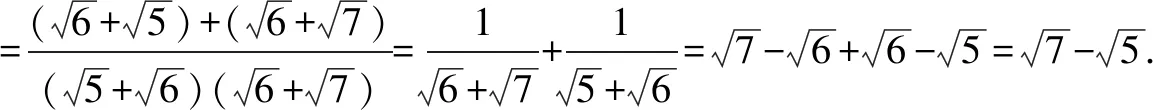
二、运用逆运算

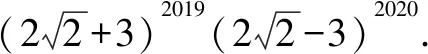
解析本题的关键是巧用积的乘方的逆运算：anbn=(ab)n.

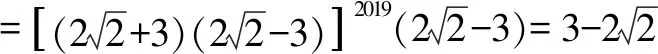
三、换元思想

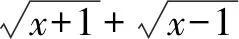
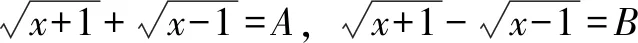
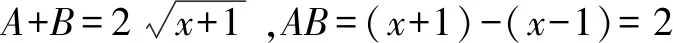
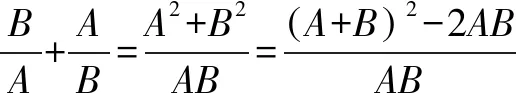
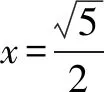
当二次根式结构复杂，可以通过换元，将结论的形式转化为简单形式，以便于发现解题规律.

四、构造方程

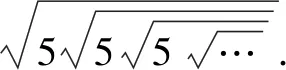
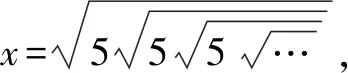
两边平方，得x2=5x，即x(x-5)=0

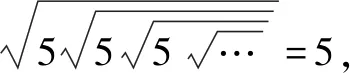
五、配方法

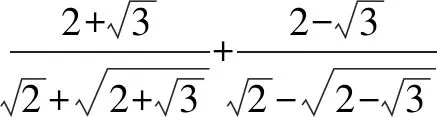
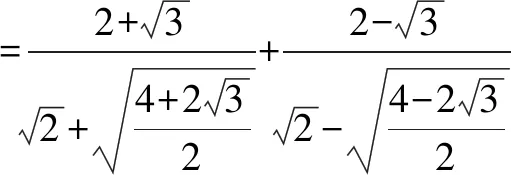
无独有偶，我们来看北京某中学高一试题;

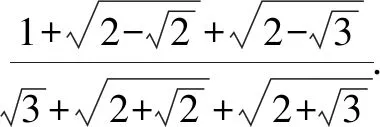
考点： 二次根式的化简.

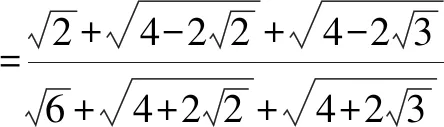
此试题其他解法.

(方法二)：运用特殊角的三角函数值求解.

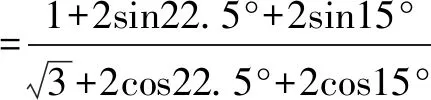
(方法三)：观察二次根式的结构特点，找出通法.

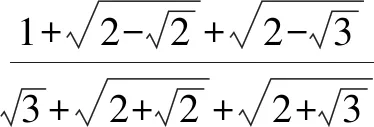
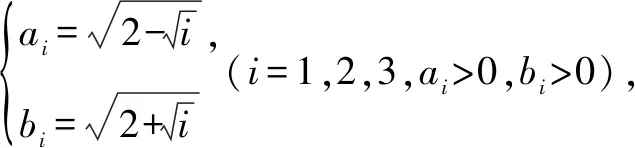
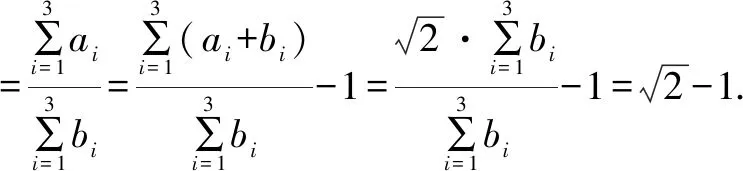
同类延伸推广.

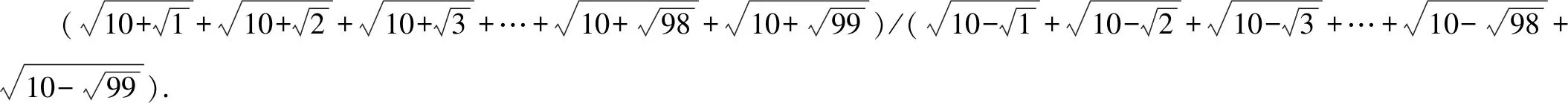
这道推广题用原题的方法，分子分母同乘某个数来化简，显然不易.

1.观察分子头尾两项二次根式的特点，采用三角函数法来化简.

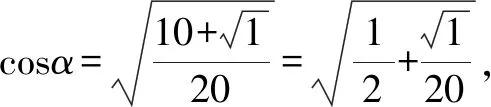
2.此类二次根式化简的通性通法.

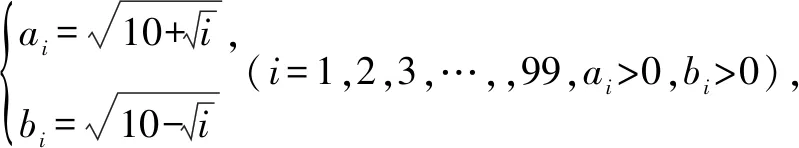
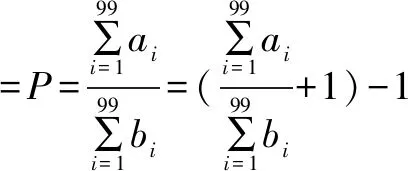
纵观二次根式化简求值，常见方法有公式法、拆项法、倒数法、约分法、配方法、平方法、换元法等，

笔者认为培养学生的运算能力，夯实基础，加强训练梯度，教师既不能以简单题重复训练为主，也不能一味将学生置于大量繁琐的复杂运算问题之中，而应以螺旋式上升为主的梯度式训练，注重观察、思考，找出通性通法，有效提高运算能力、锻炼数学思维，从而使学生具备良好的数学核心素养.