基于RRT和DWA的欠驱动UUV路径规划

严浙平，黄俊儒，吴 迪

（哈尔滨工程大学 自动化学院，黑龙江 哈尔滨 150001）

0 引言

水下无人潜航器（Unmanned Underwater Vehicle，UUV）的运动规划是UUV核心技术之一，本文重点讨论水平面规划。路径规划以功能和侧重点分为全局路径规划和局部路径规划，两者有区别但又可以相互转化。全局路径规划是在已知周围环境的前提下可以快速规划出一条最优路径，但全局路径规划有时不考虑动力学约束，并且水下环境复杂，环境信息获取并不完全，容错率较低；局部路径规划侧重于局部环境规避未知障碍物的能力，但其寻找到最优全局路径的效率低下。如何使 UUV快速安全地到达目标点是一个重要的研究方向。

全局路径规划有很多成熟的算法，早在 1958年就有了Dijsktra算法，改进后又有了A*和D*算法，以及蚁群算法、贪心算法、粒子群算法等。丁帅以减少水下机器人能量消耗为前提，基于RRT*算法设计了能耗最低的路径规划算法[1]；孙波针对移动机器人的路径规划提出了粒子群优化算法[2]；邓超针对UUV三维空间移动提出了双种群粒子群算法[3]。局部路径规划一般配备了各类传感器以获取局部地图或者探测未知障碍物，其算法也有人工势场法以及动态窗口法。同时也有衍生的改进和结合的算法：黄辰考虑到机器人的尺寸，通过激光雷达获取局部地图，改进了DWA算法[4]；何壮壮在ROS环境下提出了针对两轮机器人的 D*和 DWA结合算法等[5]。

针对欠驱动UUV的研究也比较成熟，张伟针对垂直面的路径跟踪目标设计了基于模型预测连续系统跟踪控制器，避免离散化，提高了控制器的泰勒展开阶次，提高了精度[6]。赵玉飞针对UUV近海底的路径规划问题，提出了改进粒子群算法[7]。该算法可以有效规避静态障碍物，但是无法规避动态障碍物，针对这一问题，本文提出了快速扩展随机树以及动态窗口的融合算法框架。该算法一方面继承了 RRT算法的全局规划能力，一方面继承了DWA算法的实时避障能力，实现了实时避障的全局路径规划。通过修改外部框架的距离参数可以提高全局路径的精度，同时通过修改内部框架的评价函数参数可以使UUV应对不同的需求和地形，最后设计了融合参数μ，通过修改μ来确定内外框架的融合度。

1 UUV水平面数学模型

欠驱动UUV路径规划为水平面的规划，所以不考虑垂直方向运动，水平面模型由欠驱动 UUV六自由度模型在水平面方向解耦得到。

水平面运动学模型：

水平面动力学模型：

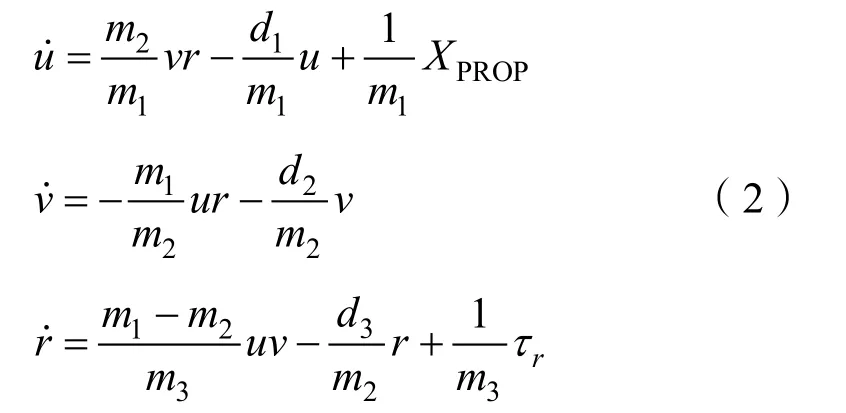
其中

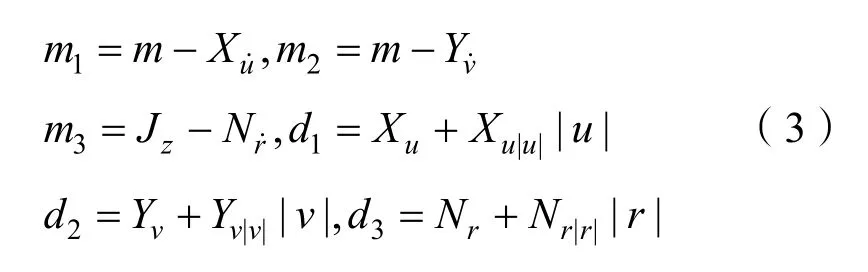
动态窗口算法中UUV未来时域的状态由状态空间模型得到，由式（1）和式（2）转换为 UUV的水平面状态空间方程：

式中：x∈R6，u∈R2，y∈R3，状态空间方程的状态量为UUV的位置姿态，输出量为UUV的实际位置坐标；x，y为UUV水平面坐标；u，v为横、纵向速度；ψ，r为艏向角和角速度；Xprop、τr为纵向推力以及转向力矩。

2 路径规划算法

2.1 RRT全局路径规划算法

在全局路径规划的算法中，快速扩展随机树（Rapidly-exploring Random Trees，RRT）算法由LaValle教授在20世纪末提出。RRT算法相对于其他全局算法的优点在于可以更快更灵活地规划出路径，并且不要求障碍物形状的规则性。但是缺点也尤为明显：它的效率并不稳定，由于其迭代过程没有目标性，所以每次的路径选取并不相同。经过类似迷宫的狭窄区域很难找到出口，需要大量反复计算，浪费时间和资源。并且所需路径越平滑，计算量也越大。一些改进的 RRT算法弥补了部分缺点，且可通过插值修正曲线。

初始化的地图只包含随机树的根节点也就是起始点Qint和目标点Qgol。首先按照策略概率p生成一个随机点Qrad，p的生成由一个随机数保证。随机树上离该随机点最近的节点Qnear（初始化的情况下为起始点）向Qrad矢量方向生成一个新节点Qnew。Qnear和Qnew的长度为距离参数qdist，修改此参数可以修改RRT算法的精度和计算量。之后对随机树上的节点Qnear以及Qnew的路线做障碍物碰撞检测，若发生碰撞则放弃此条路径，若没有发生碰撞则将节点Qnew加入到随机树节点中，Qnear和Qnew加入到路径矩阵。重复以上步骤直到Qnew与Qgol之间的距离小于设定值Qset，即说明到达目标点。最后依据贪心算法简化得到的路径，从起点Qint起依次寻找与Qgol节点满足碰撞检测函数的节点q*，用此路径替代之前的路径，再以q*为终点依次寻找得到一个最简路径。同时需要注意以下几点。

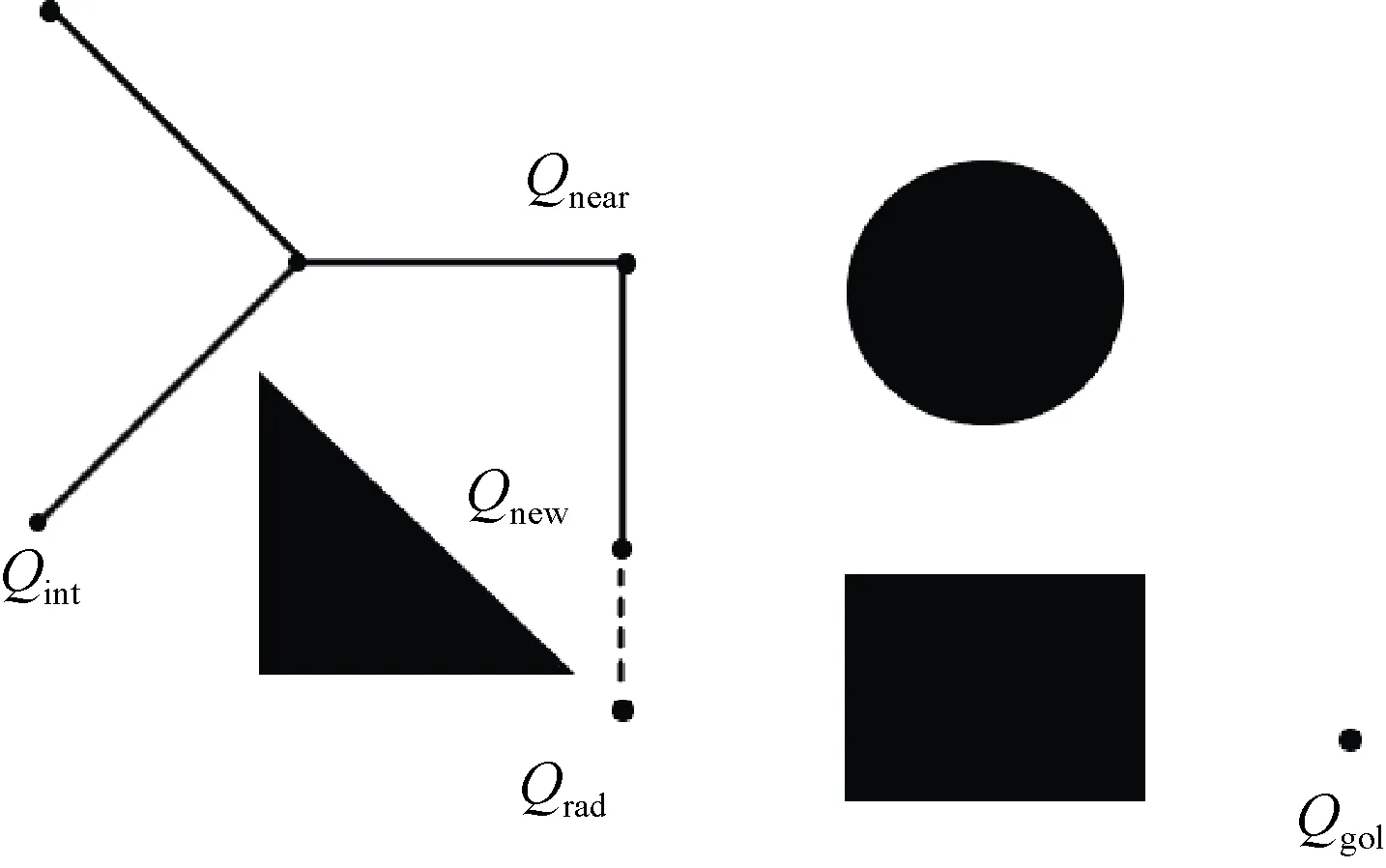
图1 RRT算法示意图Fig. 1 RRT algorithm diagram

1）策略概率p依据目标点的距离给定，以一个随机数确保概率的有效性。距离目标点越近生成Qrad的概率越高，否则随机树将聚集在一个区域，不能很好地向目标点方向伸展探索空间。p选取为

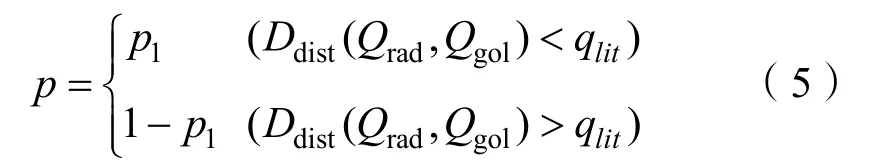
2）为了保证算法的效率和可控性，需要设定每次搜索的循环次数，在给定次数之内完成循环，否则放弃此次搜索。以下为RRT算法的具体步骤：

①加载全局地图（获取障碍物信息，给定全局路径起点Qint，终点Qgol），设置距离参数qdist，范围参数Qset；

②设置循环；

③随机生成Qrad，设置全局终点附近生成Qrad的概率p；

④选取距离Qrad最近的随机树节点Qnear向Qrad方向伸展，伸展长度为距离参数qdist，伸展后得到新节点Qnew；

⑤对Qnear与Qnew之间的路径进行碰撞检测，若此路径与障碍物存在交集则舍弃该节点，若不存在交集则将Qnew加入到随机树节点中；

⑥检测循环次数，若达到循环次数则回到③重新构建随机树，未超出次数则继续扩展随机树；

⑦检测Qnew与Qgol之间的距离是否小于Qset，若小于说明到达目标点则跳出循环，并输出随机树节点以及路径，若不小于则回到③；

⑧通过碰撞检测简化输出的随机树节点和路径。从起点依次寻找与终点Qgol满足未碰撞的节点，找到未碰撞的节点q*后即舍弃该节点之后的节点，简化此节点到终点的路径，以此节点为终点重复以上过程继续向前寻找未碰撞节点得到最简路径。

2.2 DWA局部路径规划算法

相对于全局路径规划来说，局部路径规划并不要求对周围环境百分之百的了解。全局路径规划为移动机器人在已知全局地图的前提下规划出从一个区域到另一个区域的具体路线，而局部路径规划的地图多为临时获取，由获得的局部地图规划出一条临时路线，随着机器人的移动，局部地图实时更新，路线也实时更新。局部路径规划往往和各类传感器协同工作，由传感器获取周围环境的具体信息，进而得到局部地图进行规划[8]。局部路径规划的缺点是受参数以及位置环境物体影响，随机性较高，无法生成一个固定高效的全局路线[9-10]。

动态窗口算法（Dynamic Window Approach，DWA）同样是20世纪末提出，其使用的是在线规划的方法：根据机器人本身的运动学模型得到各类约束，利用运动学约束根据当前的状态得出下一拍的动态区域，区域内包括机器人下一拍能实现的全部运动轨迹和状态。常用的移动机器人运动学模型在相邻拍数的轨迹一般用直线代替，用圆弧代替相比于直线更精确一些，而UUV的受力十分复杂，需要UUV专用的模型。之后通过对区域内的所有轨迹进行评价分析，得到一条得分最高的即为最优轨迹。

DWA算法的核心主要有2部分，第1部分为动态窗口的生成，依据以下几点。

1）速度与角速度约束，由UUV本身的性能得到最大与最小速度。

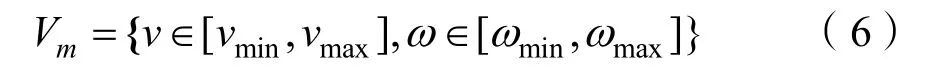
2）加速度约束，UUV的加速度受螺旋桨的推力以及水流情况的影响，所能达到的最小与最大加速度，在一拍时间内与最大最小速度和角速度共同组成了一个轨迹范围，生成了一拍时间内的动态窗口。

3）碰撞检测，为了使 UUV避免碰撞到障碍物，相应的距离需要小于对应的速度。

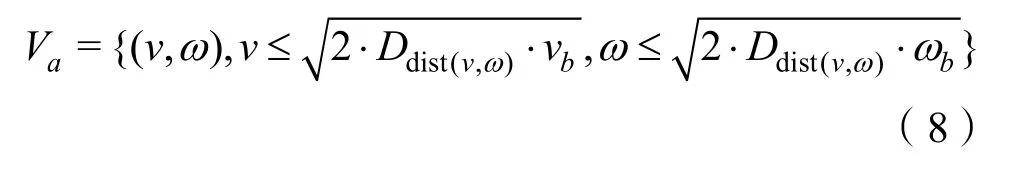
式中：Ddist(v,ω)为UUV与障碍物之间的轨迹距离，若在一定距离内小于对应速度则该条轨迹保留，否则去除该条轨迹。

第2部分为轨迹的评分策略函数G(v,)ω，根据生成的动态窗口得到若干条轨迹，分析每一条轨迹的效率和安全性，评分主要依据以下几点。

1）艏向Eheading(v,ω)评分，UUV轨迹的实际航向越接近目标方向，则该评分越高。

2）安全系数Esdist评分，UUV轨迹距离障碍物越远，则评分越高；若该条轨迹距离障碍物小于对应速度的安全距离则直接舍弃；全路路径的安全性首先由此函数检验。

3）效率Evelocity(v,ω)评分，根据UUV轨迹的曲率、角加速度以及效率进行评分，越平滑速度越快，评分越高。

由于三类分属于不同的系统，为了防止某一参数占比过高导致不同路径的评分占比差距过大，将三类评价函数统一可以得到Eevaluate(i)。

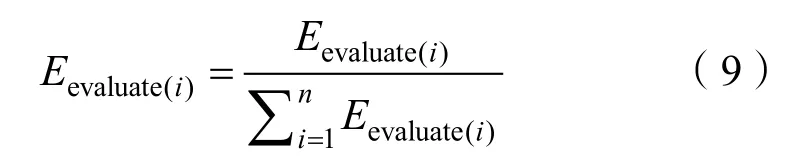
加入可调整的占比得到最终的评分函数。α为艏向评分占比，β为安全系数评分占比，γ为效率评分占比。

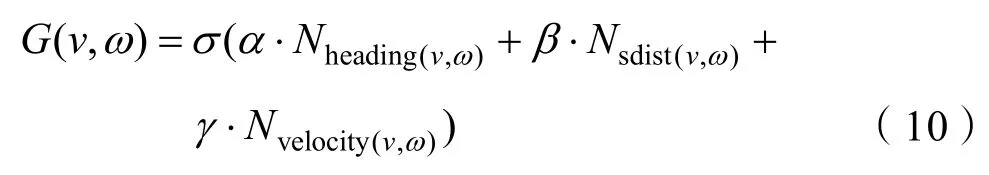
3 基于RRT和DWA的改进路径规划算法

针对全局算法和局部算法的优缺点以及UUV性能与安全性的需求，提出了RRT和DWA改进的融合算法。该算法主要有两层规划设计，一层外部框架和一层内部框架。外部框架由RRT算法实现，内部框架将由RRT算法得到全局路径分段，再由DWA在线规划。融合算法的框架如图2所示。具体流程如下：

1）首先全局框架加载全局地图，当获取到起始点和目标点信息后规划出一条全局路径。传感器进入待机状态，传感器的范围即是局部框架动态轨迹窗口的范围。

2）将得到的全局路径发送给局部框架，利用DWA算法检验全局路径是否满足 UUV的运动学规律，若不满足则重新生成全局路径。此外，当传感器得到的局部地图中有全局地图中未知的障碍物，并且此障碍物不在安全距离之外时则会发生碰撞，发出碰撞警告。

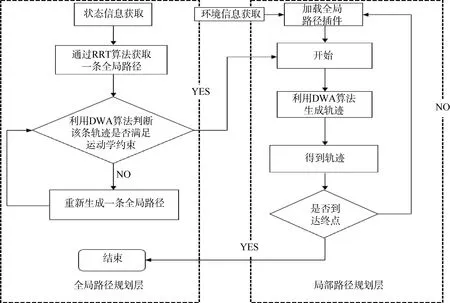
图2 RRT-DWA融合算法框架Fig. 2 RRT-DWA fusion algorithm framework

3）局部框架加载全局路径后，由融合参数μ确定全局路径插值，μ参数即为由RRT算法得到的最终全局路径的分段比例，根据路径的长短以及障碍物的密度进行修改，这里取为0.05。再由DWA算法在线生成局部路径，直到到达目标点完成循环，得到修正后的路径。

表1 动态窗口仿真参数Table 1 Dynamic window simulation parameters

4 仿真验证分析

针对以上设计的算法，构建1个1 000 m2的仿真地图，图中黑色区域为障碍物；目标的起始点为原点，终点为地图右上角。首先给定3组参数验证单独使用动态窗口的全局路径规划性能。

图3为利用DWA算法得到的路径，改变DWA算法中评价函数中艏向评分占比，安全系数评分占比以及效率评分占比将得到不同的路径。图中蓝色和绿色两条轨迹的航向角评分分别为0.5和0.45，占比较高，在（300，300）坐标附近时为保证航向角评分路径的生成朝向目标点，UUV从障碍物上方行驶。下方红色轨迹的安全性评分为0.6，占比更高，所以在同一位置为保证安全性的评分，远离障碍物，UUV向下行驶。这就导致了单纯的DWA算法受很多因素影响，很难找到一条简洁的全局轨迹。

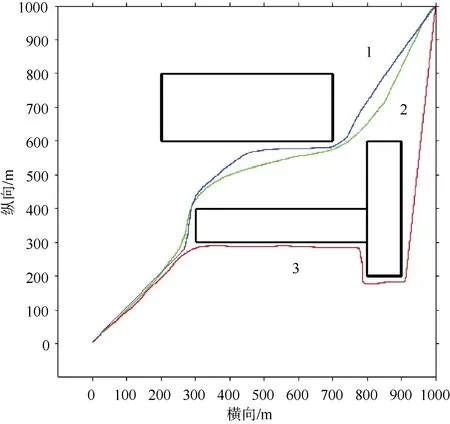
图3 基于DWA算法的局部规划Fig. 3 Local planning based on DWA algorithm

图4和图5为利用RRT算法得到的全局路径，两次生成的全局路径并不相同，说明该算法有较高的灵活性。由于 RRT算法得到的全局路径未考虑UUV的运动学约束，在图4以及图5中部分路径与障碍物相对较近，小于10 m的安全距离，安全性得不到保证。

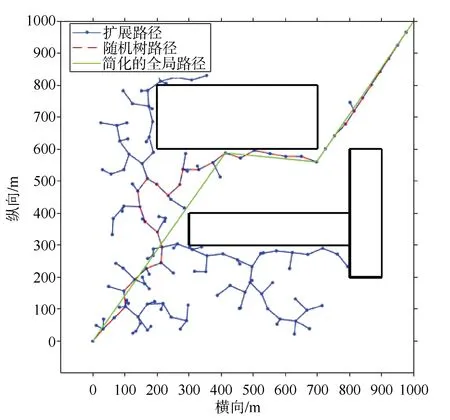
图4 基于RRT算法的全局规划（1）Fig. 4 Global planning based on RRT（1）

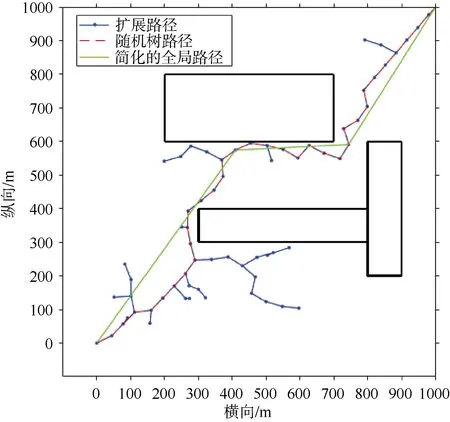
图5 基于RRT算法的全局规划（2）Fig. 5 Global planning based on RRT（2）

图6和图7为RRT-DWA融合算法生成的路径，其中绿色轨迹为图4和图5中利用RRT得到的全局路径，红色轨迹为RRT-DWA融合算法轨迹。由图可知，该条轨迹由于采用了RRT算法，其轨迹比较灵活，很容易找到一条简洁的全局路径。同时后加入的DWA算法使得该条路径满足UUV的运动学规律，可以时刻与障碍物保持距离，保证了安全，继承了DWA算法的躲避移动或未知障碍物的能力。

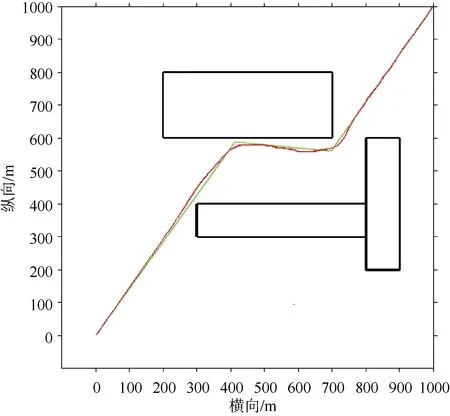
图6 基于融合算法的全局规划（1）Fig. 6 Global planning based on RRT-DWA（1）

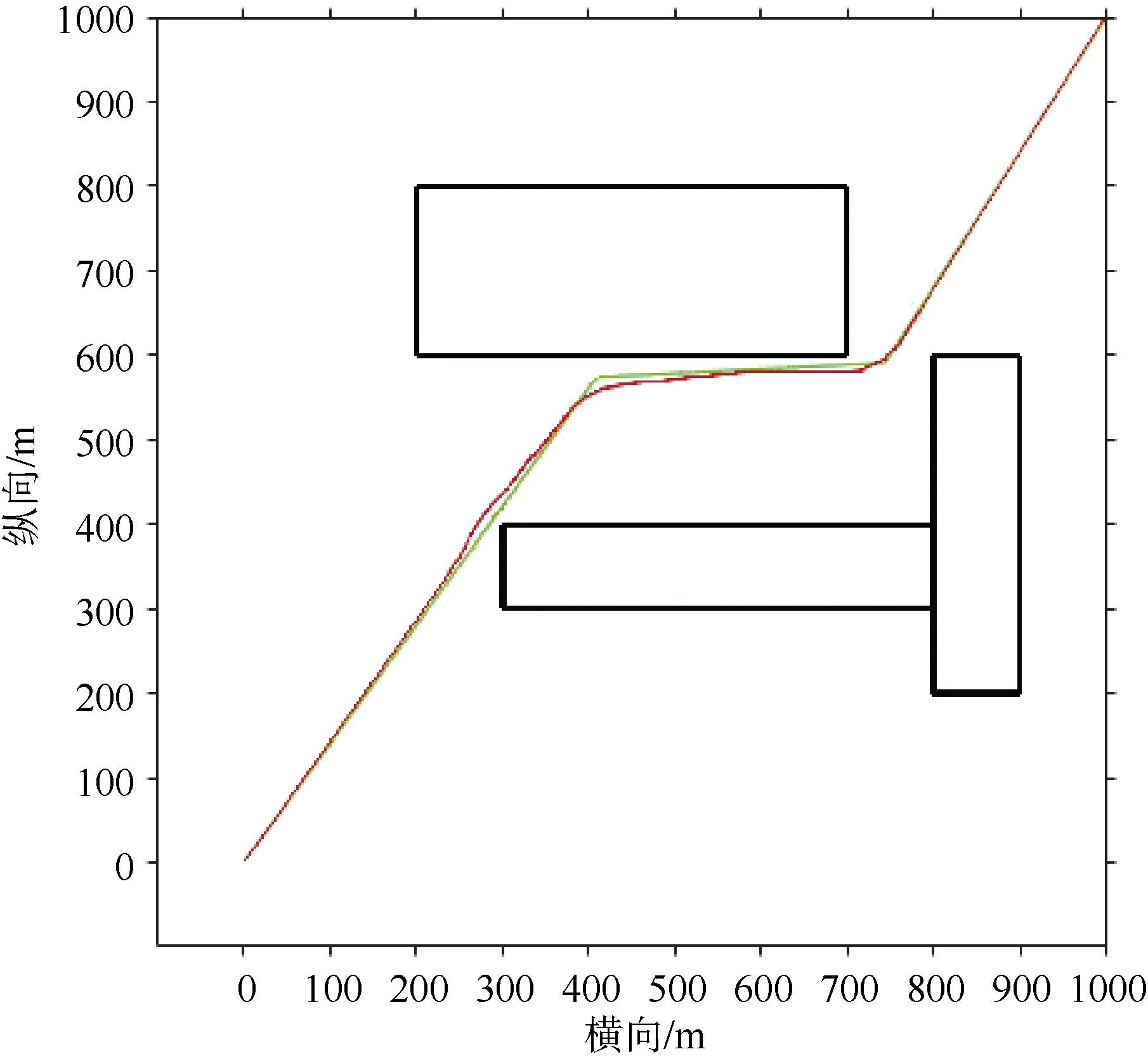
图7 基于融合算法的全局规划（2）Fig. 7 Global planning based on RRT-DWA（2）

表2中RRT1和RRT-DWA1分别对应图4和图 6中一段范围内的最近障碍物的距离，RRT2、RRT-DWA2对应图5和图7中障碍物距离。由表知RRT算法得到的轨迹无法实时保证安全距离；融合算法得到的轨迹可以始终保证10 m的安全距离，说明了融合算法具有良好的避障能力。

表2 最近障碍物距离Table 2 Nearest obstacle distance

5 结束语

为保证UUV水平面规划的效率以及安全性，以UUV水平面状态空间方程为研究对象，针对传统局部路径规划和全局路径规划导航方式的优缺点，提出了RRT-DWA融合算法。融合算法的外部框架不考虑动力学约束，仿真结果显示有较好的全局路径搜索能力和灵活性；内部框架结合UUV的运动模型、动力学模型以及传感器实时获取局部信息，通过评价函数可以实现障碍物的规避。仿真结果显示，融合算法始终可以保持10 m的安全距离，保证了安全，通过内部框架判断全局路径的可行性。同时应对不同的海底区域可以通过调整局部框架的评价函数参数来满足安全性或者效率的需求。综上，RRT-DWA融合算法可以实现以上功能，满足UUV现实需求。