考虑动力学效应的结冰试验相似准则修正方法

李维浩, 李伟斌, 易 贤,*, 王应宇

(1.中国空气动力研究与发展中心 结冰与防/除冰重点实验室, 四川 绵阳 621000; 2.中国空气动力研究与发展中心 计算空气动力研究所, 四川 绵阳 621000)

0 引 言

飞机结冰是威胁飞行安全的潜在因素之一[1]。为了满足适航要求，确保飞行安全，需要在结冰风洞中进行一系列飞机结冰与防/除冰的试验[2]。受结冰风洞尺寸和模拟能力的限制，风洞试验条件无法达到真实飞行条件，因此需要应用结冰试验相似准则对某些试验参数进行相似转换。国内外学者在结冰试验相似准则相关研究方面取得了大量成果[3-5]，从流场属性、水滴轨迹、水收集量和热力学这4个方面建立了一套完整的相似理论。21世纪以来，随着过冷大水滴(Supercooled Large Droplet, SLD)结冰逐渐受到重视，研究者发现小水滴的相似准则并不适用于大水滴[6]。Anderson[7]将小水滴相似准则应用于大水滴的结冰风洞试验，结果显示，当水滴直径大于120 μm时，缩比条件下的冰形和参考条件下的差异极大。这是由于常用的结冰相似准则都是基于水滴是刚体球这一假设推导而来的，没有考虑水滴的动力学特性[8]，尤其是在SLD结冰条件下，水滴在运动和撞击过程中存在明显的变形破碎、飞溅等现象。如果不对现有相似准则进行修正，将极大地降低SLD结冰条件下风洞试验的准确性。因此需要研究针对现有结冰试验相似准则的、考虑动力学效应的修正方法。

由于小水滴相似准则的建立是通过对运动方程和热力学方程进行量纲分析，从而推导出多个相似参数，而大水滴同样满足这些物理方程，因此现阶段SLD结冰试验相似准则的主要研究思路是在小水滴相似准则的基础上进行扩展。由于大水滴不能被视作刚体球，需要考虑液态水表面张力的影响，所以Anderson[9-10]和Tsao[11]等提出运用若干韦伯数来修正小水滴相似准则，例如以水滴直径为特征尺寸的Wed[9]、以模型大小为特征尺寸的WeL[10]以及以水膜厚度为特征尺寸的Wet[11]，这些相似参数都一定程度提高了结冰相似结果，但仍不够令人满意。国内学者对SLD结冰试验相似准则进行了初步的探索。文献[12]建立了考虑动力学特性的结冰相似准则，使用该相似准则得到的局部收集系数以及冰形与参考条件吻合较好，但不能满足水滴飞溅后二次撞击的相似要求。文献[13]使用撞击参数来修正相似准则，Kimp-ONERA法可有望发展成为准确预测SLD结冰条件下成冰构型的一种缩比方法，但是此方法仅考虑了撞击特性，未考虑除此以外的动力学特性。为了考虑多种动力学特性影响，文献[14]和[15]分别针对运动过程中的变形破碎和撞击过程中的飞溅，提出了2个综合影响参数来描述多种因素对结冰过程的影响程度。

为了提高大水滴结冰试验模拟能力，本文研究了适用于大水滴结冰相似准则的修正方法。通过量纲分析，将变形破碎和飞溅的综合影响参数无量纲化，推导出2个相似参数，将其作为相似性要求融入ONERA相似准则，提出修正的结冰试验相似准则，并采用数值模拟验证修正方法的有效性和适用性。

1 ONERA结冰相似准则

ONERA相似准则是法国航空航天研究院发展的尺寸缩比方法，该准则由以下4个相似性要求组成[14]：

(1)

其中，n为冻结比例，K0为改进的惯性参数，b为相对热因子，AC为聚集因子，下标“S”和“R”分别代表缩比试验条件和参考试验条件。式(1)中第一项和第三项可满足结冰热力学相似，第二项可满足水滴轨迹相似，第四项可满足水收集量相似。

结冰试验中，一般需要确定7个参数，包括模型尺寸l、速度V、压力p、温度T、液态水含量LWC、水滴直径d和结冰时间t。接下来介绍各相似参数的选取方式。

(1)试验速度的选取

在ONERA相似准则中，速度可以在限定范围内自由选取。为了得到更接近实际的相似结果，一般根据参考试验条件选取。其中，关于试验速度的常见选取方式有等值速度法、等韦伯数速度法、等雷诺数速度法和固定试验压力速度法等。假设风洞没有高度模拟能力，采用固定试验压力的速度法：

(2)

(2)压力的选取

在ONERA方法中，没有给出压力的约束方程，试验压力可以根据试验的需要自由选取。在没有高度模拟能力的结冰风洞中，试验压力固定为1个标准大气压。如果不考虑设备模拟能力的限制，可使用混合条件，迭代求解出试验压力。

(3)水滴直径的选取

水滴直径通过相似性要求K0,S=K0,R求得：

(3)

(4)液态水含量的选取

根据相似性要求bS=bR，可得：

(4)

(5)结冰时间的选取

根据相似性要求AC,S=AC,R，可得：

(5)

(6)试验温度的选取

根据相似性要求nS=nR，可得：

(6)

其中，θ为空气能量传递势，cp,w为水的比热。由于θ本身是温度的函数，故式(6)需要迭代求解。

2 考虑动力学效应的修正方法

此前的研究中对SLD动力学特性进行了分析。研究了SLD运动中的变形/破碎特性，对比了流场速度、水滴直径和绕流物体尺寸对变形/破碎及其效应的影响规律，分别针对变形破碎和飞溅，提出了2个综合影响参数Xb和Xs[15-16]：

(7)

(8)

其中，d为水滴直径，V∞为流场速度，rL为翼型前缘半径。研究表明，这2个参数可以体现多因素对动力学特性及其效应的影响规律，是表征变形破碎和飞溅的合适参数。

通过对水滴运动和撞击过程分析可知，动力学特性及其效应受到多个参数影响，它们之间的关系可以用以下函数来表示：

π=f(d,V∞,rL,ρa,μa,σ)

(9)

其中，π是可以表征飞机结冰的无量纲参数，例如局部收集系数、撞击极限等，σ为水滴表面张力系数，ρa为空气密度，μa为空气黏性系数。采用Xb和Xs代替d,V∞,rL，可得：

π=f(Xb,Xs,ρa,μa,σ)

(10)

式(10)中，各变量的量纲分别如表1所示：

表1 影响结冰过程的变量的量纲

其中,L代表长度量纲，T代表时间量纲，M代表质量量纲。将上表中的量纲代入式(10)得:

=L4αT-2α·L0.75βT-0.25β·MγL-3γ·

MδL-δT-δ·MεT-2ε

=L4α+0.75β-3γ-δT-2α-0.25β-δ-2εMγ+δ+ε

=1

(11)

解得:

(12)

分别令α=1、β=0和α=0、β=1,可得到2个无量纲参数:

(13)

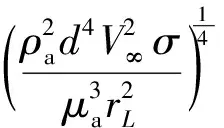
(14)

这2个相似性参数分别针对运动过程和撞击过程的动力学效应提出，因此文中以其修正现有的结冰试验相似准则。

根据这2个相似参数，可以得到2个新的相似性要求：

πb,S=πb,R

(15)

πs,S=πs,R

(16)

将式(13)和(14)分别代入式(15)和(16)可得:

(17)

(18)

上述分析中得到的2个相似性要求，在试验压强固定(标准大气压)的情况下，无法在ONERA相似准则中同时满足，所以分别采用这2个相似参数来对小水滴相似准则进行修正，具体如下：

(1)πb修正：该方法仅对SLD变形与破碎的动力学效应进行修正，即满足式(15)的相似性要求，且试验压强选取标准大气压强。

(2)πs修正：该方法仅对SLD飞溅的动力学效应进行修正，即满足式(16)的相似性要求，且试验压强选取标准大气压强。

3 修正方法有效性验证

3.1 相似结果评估方法

由于本文仅考虑动力学效应的影响，只需对比收集系数便可验证修正方法是否有效。具体的流程可以概括为：

(1)选取合适的参考条件。以弦长为1 m的MS-317翼型作为参考模型，选取具有一定海拔高度的试验条件作为参考条件。为了排除热力学的影响，结冰温度选择-20 ℃，该温度下的结冰一般为霜冰，此时冻结系数n=1。

(2)计算缩比试验条件。缩比模型的尺寸为参考模型的1/2，并将压力固定为1个标准大气压，分别计算无修正、πb修正和πs修正这3种相似方法对应的缩比条件。

(3)计算水滴轨迹。本文采用拉格朗日法计算水滴轨迹，分别使用TAB变形破碎模型和LEWICE飞溅模型来计算水滴的变形破碎与飞溅特性[15]。根据需求选取若干个水滴初始位置，求解水滴轨迹，结果用于收集系数的计算。

(4)对比验证收集系数。分别求得参考条件和缩比条件下的局部收集系数，并将它们拟合成连续曲线，进而得到收集系数的平均误差和撞击极限误差。

3.2 参考条件和缩比条件

参考试验条件如表2所示。Case 1的海拔高度约为3000 m，Case 2的海拔高度约为5000 m。

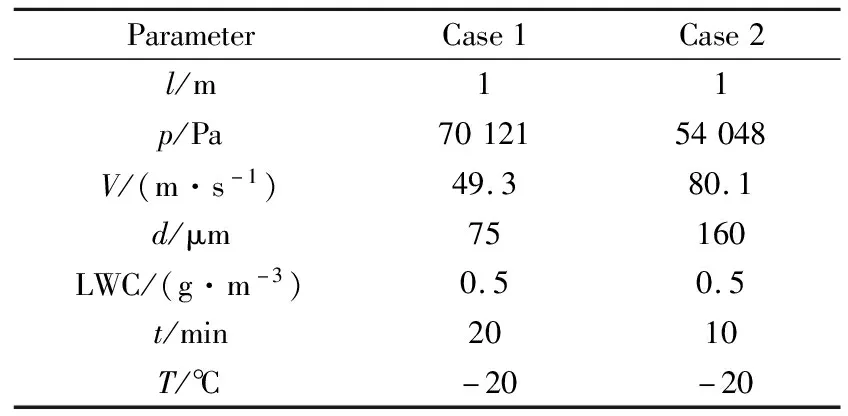
表2 参考试验条件参数

根据相似性要求，利用式(2)～(6)可计算得到有/无修正的相似准则对应试验参数，分别代入式(17)和(18)可计算得到2种修正方法对应的试验参数，如表3和4所示。

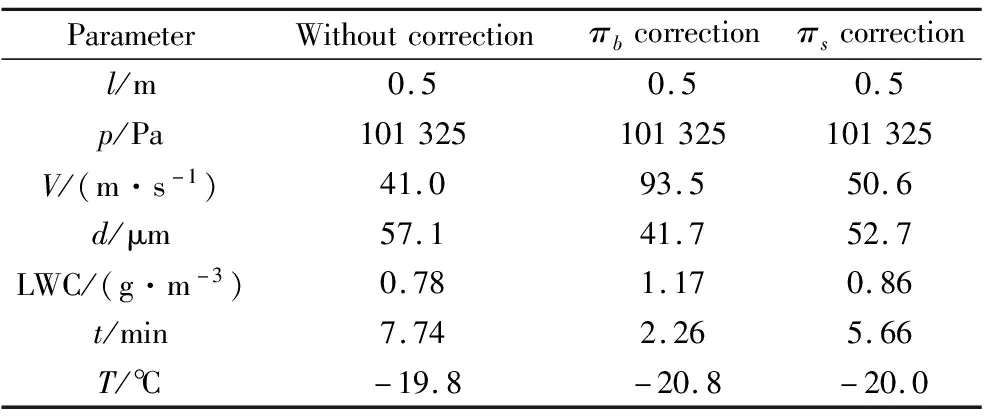
表3 缩比试验条件参数(Case 1)

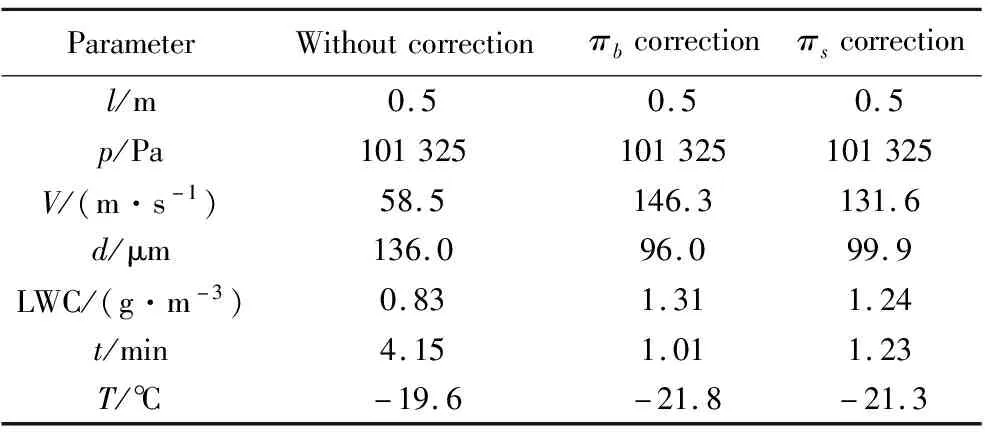
表4 缩比试验条件参数(Case 2)

3.3 计算结果对比

图1展示的是基于未修正、πb修正和πs修正等3种相似方法得到的局部收集系数与参考条件的对比结果，横坐标中ds为物面距离，c为弦长。ONERA相似准则应用于小水滴时，缩比条件的局部收集系数和参考条件的收集系数完全重合[14]，而图1显示的局部收集系数与参考条件局部收集系数还有一定差距，所以对相似准则进行修正十分必要。

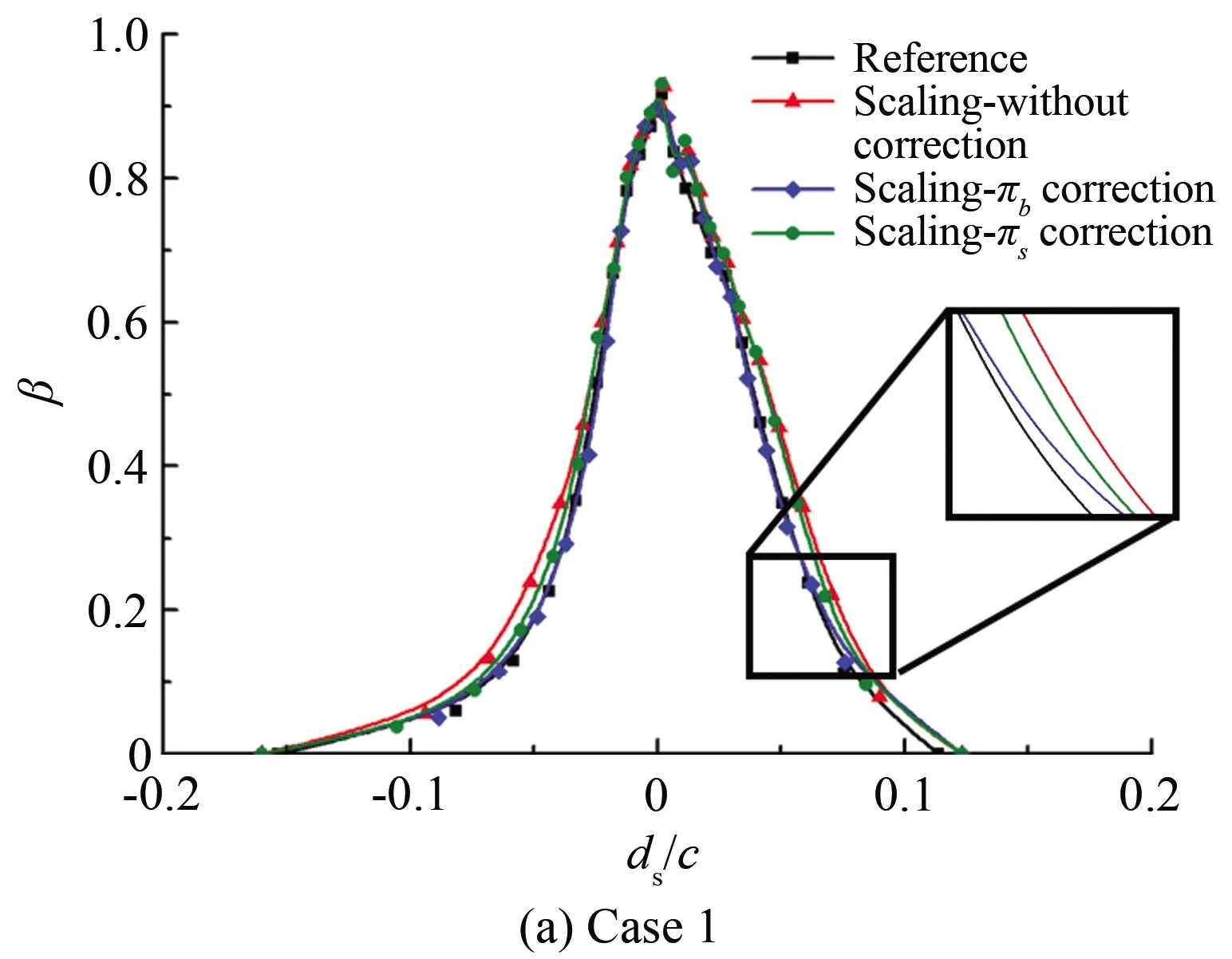
图1 参考条件与缩比条件的局部收集系数对比

由图1(a)可以看出，采用πb修正的局部收集系数与参考模型的结果几乎重合，而采用πs修正的局部收集系数与参考模型的结果存在一些差别。另外，2种修正方法在撞击极限处的误差均较大，但整体上，基于本文修正相似准则的结果较未修正相似准则得到的结果要好。

由图1(b)可以看出，2种修正方法得到的局部收集系数与参考模型的结果吻合度均非常高，说明本文方法的相似结果较好，明显优于未修正的相似准则。

为了更直观地表现这3种方法所得相似结果的优劣，计算了相似结果的误差。表5是这3种相似准则的收集系数平均误差和撞击极限误差。可以看出，无论是πb修正还是πs修正的相似准则，其收集系数平均误差和撞击极限的误差均比未修正相似准则的误差小很多，修正后相似结果得到了提高。其中πb修正得到的相似结果要优于πs修正，在不考虑风洞试验条件限制的情况下，应优先选用πb修正相似准则。

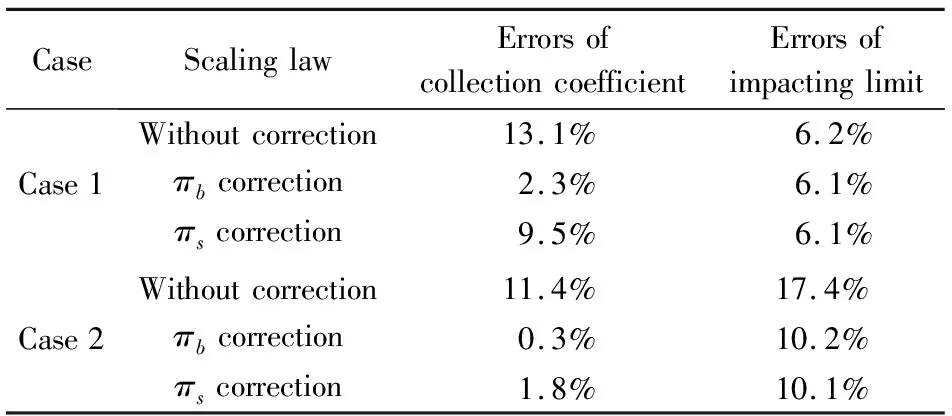
表5 修正前后相似准则误差

4 修正方法应用分析

在结冰风洞试验中，除了尺寸的限制，还存在试验条件的限制。虽然第3节中已经验证了修正后相似准则的有效性，但有可能存在计算得到的缩比条件要求过高而风洞条件无法满足的情况。本节将分析修正后相似准则在风洞试验应用中的可行性。

将试验压强固定为标准大气压强，根据相似准则的方程(2)～(5)，可以得出各参数之间在不同模拟高度的关系曲线。图2是不同模拟高度流场速度比与模型尺寸缩比的关系。可以看出，对于同一参考条件，基于πb修正的试验速度随着模型尺寸缩比的减小而增大，当尺寸缩比小于0.40时，速度比将大于2，且随着尺寸缩比的减小，速度比迅速增大，这将大大降低风洞的模拟能力；基于πs修正的试验速度随着模型尺寸缩比的减小而减小，且不同模拟高度下的速度比斜率相差较大。当尺寸缩比较大时，模拟高度为5000和7000 m的速度比较大，此时结冰风洞的模拟能力较差。

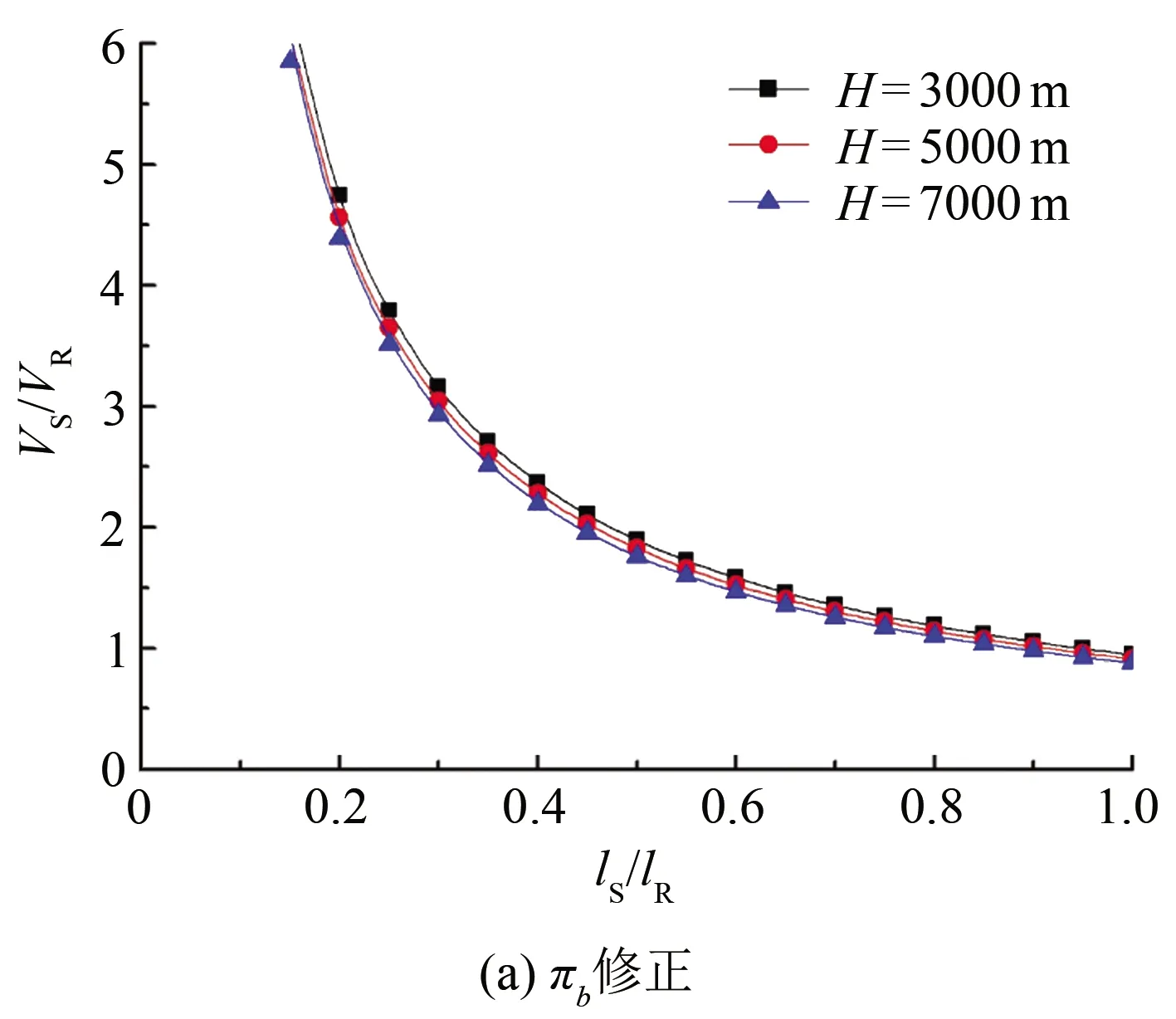
图2 流场速度比与模型尺寸缩比的关系

图3是不同模拟高度水滴直径比与模型尺寸缩比的关系。可以看出，对于同一参考条件，基于πb修正和πs修正的水滴直径随着模型尺寸缩比的减小而减小，尺寸缩比在0.05～1.00之间时，πb修正的水滴直径比在0.05～1.30之间，πs修正的水滴直径比在0.30～0.90之间，一般结冰风洞可满足直径缩比要求，而πs修正的可模拟水滴直径的范围大于πb修正。

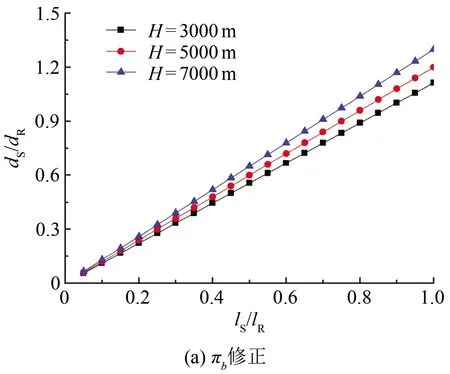
图3 水滴直径比与模型尺寸缩比的关系

图4是不同模拟高度液态水含量比与模型尺寸缩比的关系。从图中可以看出，对于同一参考条件，基于πb修正的试验液态水含量随着模型尺寸缩比的减小而增大。当尺寸缩比小于0.40时，液态水含量比将大于4，且随着尺寸缩比减小，液态水含量比迅速增大，这将大大降低风洞的模拟能力；基于πs修正的试验液态水含量随着模型尺寸缩比的变化不大，且不同模拟高度下液态水含量比相差较大，模拟高度越高，要求的试验液态水含量越高，将降低风洞的模拟能力。

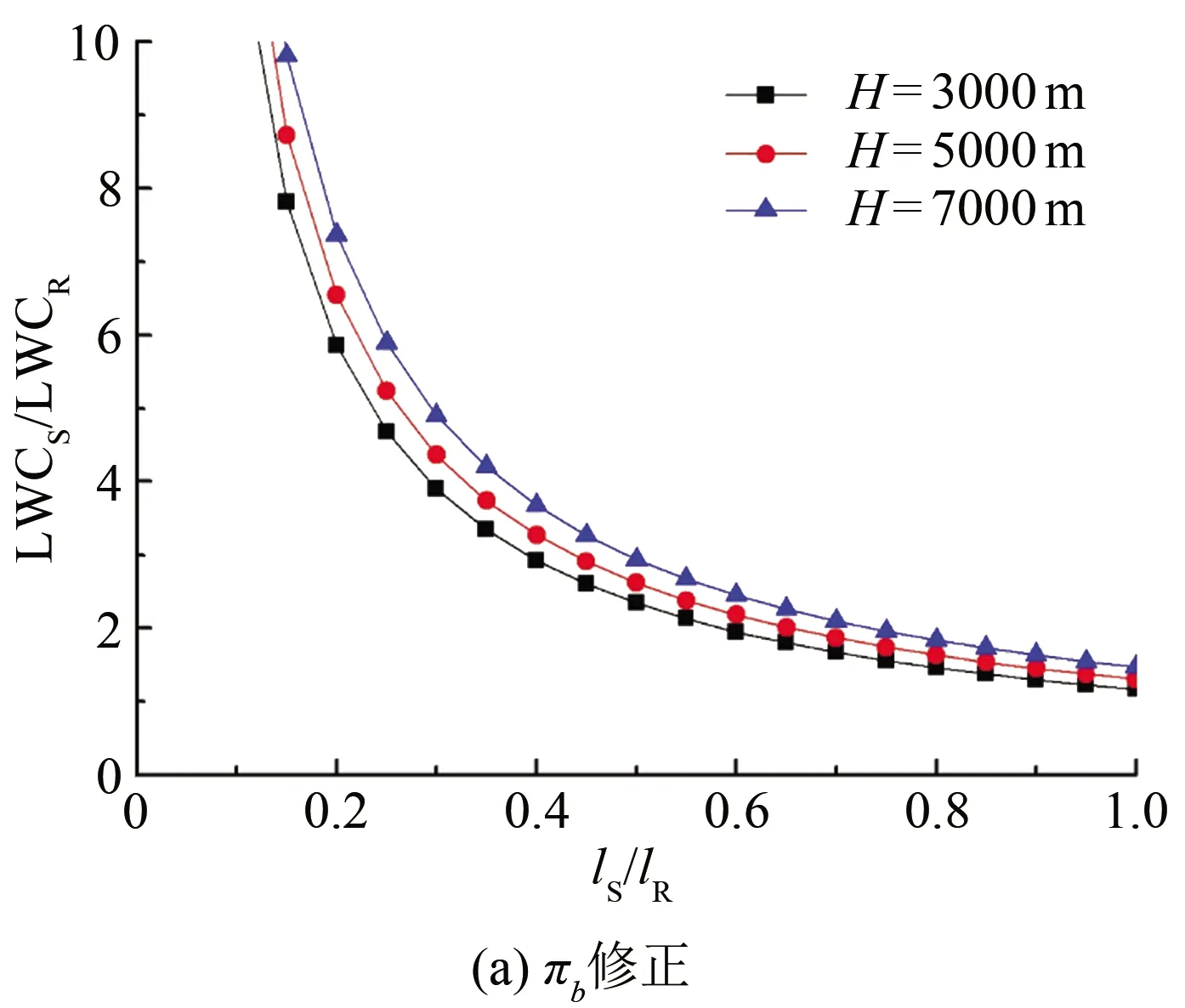
图4 液态水含量比与模型尺寸缩比的关系

图5是不同模拟高度结冰时间比与模型尺寸缩比的关系。可以看出，对于同一参考条件，基于πb修正的试验时间随着模型尺寸缩比的减小而减小；基于πs修正的试验时间随着模型尺寸缩比的变化不大，且不同模拟高度下试验时间比相差较大，模拟高度越高，要求的试验时间越短。结冰时间比均小于 1.0，说明试验时的结冰时间要小于对应的飞行结冰时间。

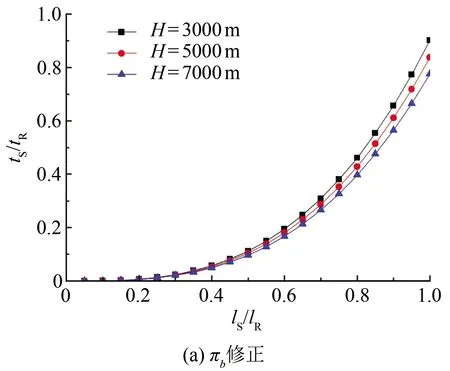
图5 结冰时间比与模型尺寸缩比的关系

通过以上分析可知，对于πb修正相似准则，当尺寸缩比小于0.40时，流场速度比和液态水含量比均较大，且随着尺寸缩比减小，2个比值迅速增大，导致可模拟的速度和液态水含量范围十分有限，所以πb修正仅适用于尺寸缩比较大的情况;对于πs修正相似准则，当尺寸缩比较大时，部分模拟高度条件下流场速度比较大，但是在结冰试验中很少采用这一范围的尺寸缩比，故对结冰风洞的模拟能力影响较小。

5 结 论

本文开展了考虑水滴变形破碎和飞溅等动力学特性的结冰相似准则研究，通过无量纲分析，提出了2种基于不同动力学效应的结冰试验相似准则修正方法，并验证了修正方法的有效性，分析了方法的可行性，得到以下结论：

(1)经数值计算验证可知，基于πb修正和πs修正的相似准则，与未修正的相比，相似结果精度都有所提高，且πb修正的相似结果优于πs修正。

(2)使用这2种修正方式时需要进行综合考虑。在试验条件允许的情况下，应优先使用πb修正相似准则；当尺寸缩比很小或者某个试验参数超出设计范围时，可选择πs修正相似准则。

目前结冰风洞的SLD模拟能力还不能完全达到要求，文中提出的修正方法无法通过试验验证，后续将结合试验结果开展相应的改进研究。