三种方法确定济南夏季日最大边界层高度的对比研究

王栋成，汤子东，邱粲,2，曹洁，董旭光

(1.山东省气候中心，山东 济南 250031；2.上海师范大学地理系，上海 200234)

引言

在大气边界层特征物理参数中，边界层高度(HBL)是最为重要的参数之一，它不仅决定着一个地区的大气环境容量或大气自净能力[1-2]，而且还强烈影响着云和对流发展及演变过程，同时也是空气质量监测和天气预报中最为重要的物理参数之一，是数值天气预报模式初始化十分关键的因素[3-5]。HBL对于天气、气候和大气污染研究是一个至关重要的参量[6]。污染扩散等大气环境过程深受边界层特性的影响，如大气边界层流动、湍流、稳定度、HBL及日变化等，其中HBL参量尤为重要，它指示了污染物在垂直方向上的扩散和稀释能力[7]。日最大HBL，又称为最大混合层厚度，它所表示的是一天中空气混合较强的最大高度，它越厚，则稀释和扩散空气中污染物质的能力就越强，反之则越弱，因此研究它对于预报空气污染潜势有重要意义[8]。

目前，获得日最大HBL的传统方法，主要可分为三类[9-15]：一是以地面气象资料为基础的经验公式法，如国标法[1,14-17]、罗氏法[14,18]、联合频率法-罗氏法B[14]、萨默斯(Summents)法[14]等，该类方法实用性强，资料易得且数据量大，但由于HBL变化的复杂性和以地面常规观测资料判断边界层变化的局限性，各种参数化方案的准确性有待进一步验证和改进[9-13]；二是以探空气象资料为基础的廓线测量法，如干绝热曲线法[19-22]、实测法[14]、风速极值法[23-25]、位温法[14,26](虚位温梯度法[3,27-28])、湿度梯度法[3,29]、湍流能量法[10,25]、综合评定法[30]等，廓线测量是确定大气边界层结构最常用的方法，可较准确地判断HBL，但由于大气边界层的特性和结构不是常规气象观测的内容，因此对它的研究依赖于特定的试验项目或每日2～3次的L波段雷达探空，观测资料在时间和空间上都非常有限[7]；三是以数值模式参数化为基础的模拟方法，即基于湍流理论的多种大气边界层参数化方案结合数值模式来预报HBL[31-34]，如最常用的中尺度气象模式WRF(Weather Research and Forecasting Mode)中有13种边界层方案，虽然各方案都能模拟出HBL的日变化特征，但在不同的下垫面及天气条件下，各方案在模拟HBL时往往存在不同程度的误差[35]。可见，廓线测量应是获得HBL及相关参量最可靠的方法，也是验证、修正及改进经验理论计算和数值模拟方法与结果的根本依据。

近年来，快速发展的风廓线雷达(wind profile radar，WPR)[36-37]、激光雷达[38-40]、微波辐射计[40]等，可实现连续系统且高时空分辨率获取大气边界层各参数的分布数据，显示出优越性，边界层的观测研究进入了一个新时代[25]。其中，WPR能够快速、细致地反映边界层的结构、厚度、湍流演变过程特征[36]。WPR产品数据中的大气折射率结构常数(Cn2)是表征湍流变化强弱的一个重要参数，Cn2与气温、气压、湿度密切相关，且随着高度的增加呈指数递减规律[36]，并表现为在边界层顶出现极大值或者偏离正常值幅度大值[25,36-46]，从Cn2垂直廓线的时间序列中可以判定HBL[36]。对流边界层顶部的夹卷过程造成温度和湿度垂直梯度增强，导致这一层的折射率结构常数Cn2变高，Cn2的这种垂直分布特征经常被用来定位出HBL[6]。现阶段基于WPR资料进行HBL确定的研究尚较少，且多属方法探索、个例或短期分析。国外如，BIANCO and WILCZAK[28]提出了基于Cn2等综合指标的模糊逻辑判别方法确定对流HBL，并给出了三天的结果对比；HEO et al.[41]提出了联合使用Cn2和垂直速度方差估计对流HBL的新方法，并对其适用性进行了初步分析；BIANCO and WILCZAK[28]对模糊逻辑判别方法进行了改进，并提供了个例验证；ALLABAKASH et al.[43]采用改进的模糊逻辑方法给出了Gadanki测站两年各月07—20时对流HBL日变化。国内如，曹晓彦等[44]、王敏仲等[45]、蒋德海等[46]、张坚[25]、金莉莉等[10]、王栋成等[11]对Cn2极大值法及求导后放大跃变特征的偏离度法等进行了方法研究或个例验证，张哲等[6]对比分析了Cn2最大后向散射法、改进后的Cn2和垂直速度方差相结合法两种方法的适用性，但均尚未系统深入研究最大HBL的较长时期的统计特征和演变规律。

本研究针对WPR偏离度法[11]、L波段雷达探空干绝热曲线法[19-22]、国标法[1,14-17]三种方法各自确定的济南夏季同期日最大HBL进行对比，分析最大HBL的统计特征和演变规律，研究其与各气象条件的相关性，并评估比较三种方法的优缺点，以期为改进HBL的各种确定方法、研究大气边界层精细化结构与大气污染的关系，提高环境空气质量预报和大气自净能力判定的准确率等提供更好的参考依据，为推动边界层理论研究、实践及应用做出有意义的探索。

1 资料与方法

1.1 资料来源

研究采用的2014年6月1—30日和7月15—24日逐小时整点后18 min、高度层100～3 940 m的Cn2等数据，来自济南WPR站(经度：117°33′E，纬度：36°41′N，海拔121.8 m)实时每6 min产品数据ROBS文件。该站固定式边界层WPR型号为CLC-11-D型，主要技术指标：雷达工作频率为1 280±20 MHz，探测数据时间分辨率r≤6 min，有效数据最低探测高度为100 m、最高探测高度h≥3 km，雷达工作模式包括低模式(分辨率为30、60、120、240 m)、高模式(分辨率为60、120、240 m)，输出产品数据的高度分辨率为60 m(820 m以下)、120 m(820～2 020 m)、240 m(2 020 m以上)三种。济南WPR站2014年Cn2产品数据非原始值，而是10×log(Cn2)且取整后的结果，Cn2突变值被削平无法用以判断HBL，本研究基于该站经质量控制后业务上传的原始产品数据和WPR设备参数等，采用中国气象局《风廓线雷达通用数据格式(V1.2)》《风廓线仪功能规格需求书(试行)》《风廓线雷达观测规定(试行)》、QX/T 78—2007《风廓线雷达信号处理规范》等推荐的雷达气象散射方程(Keeler，1993)[36]，对逐6 min的Cn2数据进行重新计算，并经一致性平均、时空连续性检验质量控制[37]，按通用数据格式的要求统一定标输出。实测Cn2廓线数据常出现个别高度层值缺测为0、连续2层以上为同一个数值、异常大值或小值等现象，根据气象场的变化是有连续性的气象原理[47]，在各高度上进行上下层、在时间上进行前后3个时次的数据奇异点判断，剔除异常数据并用前后或上下点平均来替代该点的数据，可以得到较为完整连续的随高度变化的Cn2廓线。另外，因WPR低模式、高模式探测衔接问题，940、2 020 m层Cn2数据常为较大值，导致单一特征高度层的Cn2偏大，对此采用上、下层内插方法暂替代异常值[11]。

采用的2014年6月1—30日和7月15—24日每日07、13、19时整点后15 min、高度层0～4 000 m的气温、气压、湿度、气压、虚温等数据，来自济南L波段雷达波段探空雷达记录文件。L波段雷达探空数据均经质量控制，符合《常规高空气象探测规范》[48]。L波段雷达探空秒级和分钟级数据的高度分辨率分别为6～7 m、400 m，考虑L波段雷达整点后15 min开始探测，气球按照400 m·min-1上升，10 min上升的高度足以涵盖WPR探测每6 min、100～3 940 m的高度范围，因此本研究采用的整点后18 min的ROBS数据与整点后15 min的L波段雷达探空数据的时空匹配基本一致。每10 m高度层间隔的各数据，利用L波段高空气象探测系统数据处理软件内插获取[49]。

采用的2014年6月1—30日和7月15—24日每日地面气象观测逐小时气温、地表温度、风速、降水数据，以及总低云量和日最高气温等数据，来自章丘国家基本气象观测站，数据均经自动、人工审核与质量控制，符合《地面气象观测规范》[50]要求，其中总低云量采用内插法得到逐小时值[2]。章丘国家基本气象观测站与济南WPR观测站、济南L波段雷达探空观测站属于相同站场，观测场经纬度、海拔高度基本一致，本文统称为济南站。

1.2 济南夏季日最大HBL的三种确定方法

考虑实用性和可操作性，本研究选择采用以下三种方法，各自确定济南2014年夏季6月1—30日和7月15—24日共40 d的逐日最大HBL，并进行对比分析。

方法一：偏离度法，基于WPR观测的Cn2，将每一时次的10×log(Cn2)廓线的实测值与其拟合曲线值的差定义为偏离度，实际偏离度最大值对应的高度层判断为该时次的实测HBL[11]，然后将每日07—19时的逐小时结果，排序筛选得到日最大HBL。

方法二：干绝热曲线法，在温度-高度图上，从每日地面最高气温所在点沿干绝热线上升，与当日07：15的L波段雷达探空温度廓线相交，所得交点距地面的高度即为直接估算的当日最大HBL[19-22]。

方法三：国标法，根据GB/T 13201—91《制定地方大气污染物排放标准的技术方法》[16]，基于地面气象观测的总云量、低云量和距地面10 m高度风速(U10)，通过计算太阳高度角，再查算出Pasquill大气稳定度等级，然后采用公式计算HBL=as×U10/f(as为不同大气稳定度对应的混合层系数，f为地转参数)[1,14-17]，最终计算出每日07—19时的逐小时HBL，排序筛选得到日最大HBL。

因WPR对雨滴很敏感[3,37]，当降水出现时各高度层的Cn2均明显增大，所以当有雨时HBL无法判别。本研究也证实，地面或空中降雨时段、各高度层相对湿度连续较大时段(多高度层连续大于85%以上)，WPR观测的Cn2数据均不适用于判定HBL，即方法一适用性有局限；同时L波段雷达探空数据也不适用于判定HBL，即方法二适用性同样有局限。因此，首先剔除这两种因素影响的样本，然后得到三种方法确定的日最大HBL样本数共3×25个，同样得到方法一和方法三确定的逐小时HBL样本数共2×303个，基于此进行统一对比分析。

2 结果分析

2.1 三种方法确定的日最大HBL对比

三种方法确定的日最大HBL结果对比及相关分析分别见图1、2，图2中若其中二者逐日结果对应相同则所有点应分布在从左下角到右上角的对角线上(下同)。

图1 三种方法确定的济南2014年6—7月25 d各日最大HBL对比Fig.1 Comparison of the daily maximum HBL determined by the three methods in Jinan in 25 d from June to July 2014

1)偏离度法、干绝热曲线法、国标法三种方法确定的济南夏季25 d的日最大HBL平均值分别为2 500.0 m、2 529.1 m、2 469.9 m，三种方法总体一致、差异较小，偏离度法与后两者分别相差-29.1 m、+30.1 m。25 d同日期的日最大HBL比较，偏离度法、国标法分别与干绝热曲线法的日最大偏差为+722.6 m(6月6日)、+928.2 m(6月3日)，标准偏差(σ)分别为337.1 m、485.4 m，显示国标法的偏差较偏离度法的大；且国标法与偏离度法的日最大偏差+1 079.9 m(6月3日)、σ=636.7 m更大(图2)。

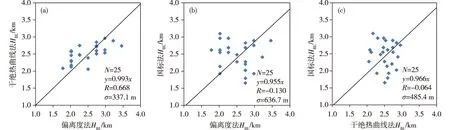
图2 三种方法确定的济南2014年6—7月25 d各日最大HBL相关性对比(a.偏离度法与干绝热曲线法的相关性，b.偏离度法与国际法的相关性，c.干绝热曲线法与国际法的相关性)Fig.2 Comparison of correlations of the daily maximum HBL determined by the three methods in Jinan in 25 d from June to July 2014 (a. correlation between the deviation degree method and the dry adiabatic curve method, b. correlation between the deviation degree method and the national standard method, c. correlation between the dry adiabatic curve method and the national standard method)

2)偏离度法与干绝热曲线法结果的相关系数R较高，为0.668(图2a)，通过0.01信度检验，说明两方法确定的25组日最大HBL相关性较好。但国标法与偏离度法、干绝热曲线法结果的R均为负值，分别为-0.130、-0.064(图2b、c)，均未能通过0.10信度检验，相关性不好。两组基于探空实测资料诊断确定的日最大HBL相关性较好，但均与基于地面观测资料半经验公式计算的HBL相关性不好，显示国标法并不能很好地反映HBL实时变化的实际状况。

3)基于实测资料确定日最大HBL，应是获得HBL及相关参量最可靠的方法，虽然偏离度法、干绝热曲线法，不同确定方法的结果会有一些差异，但两者总体上都有较好的代表性。囿于国标法是基于多年均值的地面风向、风速、稳定度联合概率分布推导的[17]，原理上该方法只适用于平均状况下的HBL估算，而对于实时HBL的判定准确度低、代表性也相对较差。

2.2 偏离度法与国标法两种方法确定的HBL演变规律对比

干绝热曲线法只能给出直接估算的每日最大HBL，并不能给出其出现的确切时间，而其他两种方法可给出。偏离度法和国标法确定的25 d每日07—19时逐小时的HBL演变分别见图3a和图3b，日最大HBL出现时间对比见图4，同时在图3中给出了07、13、19时L波段雷达探空实测虚位温梯度法[3,11,27-28]的确定结果，以进行对比。

图3 偏离度法(a)和国标法(b)确定的济南2014年6—7月25 d 中07—19时逐小时HBL演变Fig.3 Evolution of the hourly HBL determined by the deviation degree method (a) and the national standard method (b) in Jinan from 07:00 to 19:00 in 25 d from June to July 2014

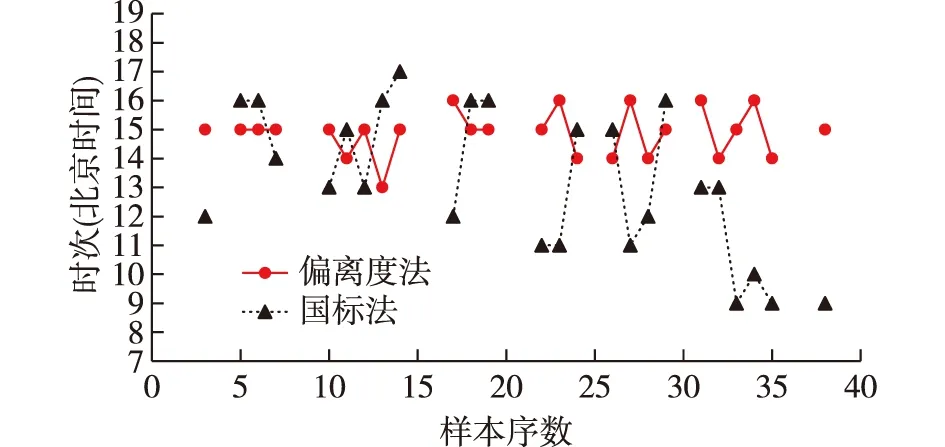
图4 偏离度法和国标法确定的济南2014年6—7月25 d日最大HBL出现时间对比Fig.4 Comparison of the occurrence time of the daily maximum HBL determined by the deviation degree method and the national standard method in Jinan in 25 d from June to July 2014

1)方法一(偏离度法)确定的济南夏季日最大HBL为3 460.0 m，出现在6月6日15时(图3a)；25 d的逐小时HBL最大值出现时间相对集中，在午后13—16时均有出现(图4)，其中以15时最多，为13 d(占比52.0%)，其次是14时6 d(占比24.0%)、16时5 d(占比20.0%)、13时1 d(占比4.0%)，符合对流边界层演变的一般规律[23,33,35]。25 d平均的HBL(图3a)，最大值2 360.8 m出现在15时，07—15时HBL呈缓慢增高态势，而15—19时HBL则快速降低。逐日实时和25 d平均的HBL演变规律基本一致，但25 d各日HBL逐小时值是波浪起伏式变化的，而非平均值那样的持续增高或降低，07—15时HBL总体呈现缓慢增高态势，而15时后有一些HBL是断崖式降低的，如6月3、6、24、28日和7月19、22日等，而另一些则是延续滞后至16时才迅速降低的，如6月17、23、27日和7月15、16日等。分析原因是，对流边界层的形成阶段是由于热力抬升增强导致的热泡式起伏增长，而崩溃阶段则是热力抬升减弱导致坍塌式快速降低[3]。

2)方法三(国标法)计算的济南夏季日最大HBL为3 099.9 m，出现在6月3日12时(图3b)；25 d的逐小时HBL最大值出现时间相对分散，在09—17时均有出现(图4)，其中以16时最多，为6 d(占比24.0%)，其次是13时4 d(占比16.0%)，09、11、12、13、15时均为3 d(占比12.0%)，10、14、17时均为1 d(占比4.0%)。25 d平均HBL最大值为1 976.7 m，出现在16时，07—12时HBL缓慢增高，16—19时HBL快速降低(图3b)。逐日实时和25 d平均的HBL演变，都在午后13—15时出现坍塌现象(图3b)，且自13时开始与偏离度法、L波段雷达探空虚位温梯度法的结果也差异较大，这与对流边界层演变的午后峰值规律显著不同。分析原因是，受近地面观测风速和近地面大气稳定度等级的影响权重过大，导致国标法估算的实时HBL准确度低，尤其是在午后峰值时段不适用，如6月11、17、22、24、27、29日和7月18日等(图3b)，其中6月27日14时距地面10 m高度的风速为0.4 m·s-1，大气稳定度等级为D类，国标法计算HBL仅为87.3 m；而偏离度法确定的14时HBL为2 020 m，L波段雷达探空虚位温梯度法确定该日13：15的HBL为1 740 m，干绝热曲线法确定的该日午后最大HBL为2 505.1 m。

3)偏离度法与L波段雷达探空虚位温梯度法确定的HBL平均值在早晨、中午、傍晚均基本一致(图3a)，两者07、13、19时的差值均很小，分别为+28.4 m、+24.3 m、-29.2 m；而国标法与L波段雷达探空虚位温梯度法确定的HBL平均值仅在傍晚基本一致(图3b)，早晨、中午则差异较大，两者07、13、19时的差值分别为+220.0 m、-385.3 m、-43.1 m。

2.3 不同方法确定的日最大HBL与各气象条件的相关关系

2.3.1HBL与气温、地表温度、风速的相关关系

1)三种方法确定的济南2014年6—7月25 d的日最大HBL，其中与日最高气温的相关性最好的是干绝热曲线法(R=0.965)，其次是偏离度法(R=0.693)，而国标法最差(R=-0.067，未通过0.05信度检验，即不相关)；与日最高地表温度的相关性最好的是干绝热曲线法(R=0.736)，其次是偏离度法(R=0.423)，而国标法最差(R=0.340，未通过0.05信度检验，即不相关)；但是，与距地面10 m高度风速的相关性最好的是国标法(R=0.880)，而偏离度法(R=-0.148)和干绝热曲线法(R=-0.085)都较差，未通过0.05信度检验，即不相关(图5)。

图5 三种方法确定的济南2014年6—7月25 d中日最大HBL与各气象要素的相关性对比(a1/a2/a3.偏离度法，b1/b2/b3.干绝热曲线法，c1/c2/c3.国标法；a1/b1/c1.日最高气温，a2/b2/c2.日最高地表温度，a3/b3/c3.距地面10 m风速)Fig.5 Comparison of correlations between the daily maximum HBL determined by the three methods and various meteorological elements in Jinan in 25 d from June to July 2014 (a1/a2/a3. the deviation degree method, b1/b2/b3. the dry adiabatic curve method, c1/c2/c3. the national standard method; a1/b1/c1. the daily maximum air temperature, a2/b2/c2. the daily maximum surface temperature, a3/b3/c3. wind speed at 10 m)

2)两种方法确定的25 d每日07—19时逐小时的HBL，其中偏离度法HBL与气温、地表温度的相关性25 d总体均较好，R分别在0.521～0.970、0.542～0.958之间，较为稳定一致、波动幅度小，且均通过0.05信度检验；但是，偏离度法HBL与风速的相关性总体较差，R在-0.673～0.919之间，不稳定且波动幅度大，仅有8组(占比32.0%)通过0.05信度检验，其余17组均未通过(图6a)。国标法HBL与气温、地表温度的相关性25 d总体均较差，R分别在-0.330～0.778、0.091～0.872之间，不稳定且波动幅度较大，分别有10组(占比40.0%)、14组(占比56.0%)通过0.05信度检验，其余15、11组均未通过；国标法HBL与风速的相关性总体较好但不稳定，有20组(占比80.0%)通过了0.05信度检验且R在0.568～0.959之间，其余5组未通过且R在-0.513～0.411之间(图6b)。

以上结果是三种方法的确定原理和采用的基础资料的直接反映，偏离度法确定HBL是基于WPR观测的高空的Cn2，判定时与地面气象要素没有直接计算关联；干绝热曲线法确定HBL则借助于每日地面最高气温，故与气温的相关性最好；而国标法确定HBL则直接引用距地面10 m高度的风速计算，故与风速的相关性最好。由于影响HBL的主要因素是太阳直接辐射，太阳直接辐射加热地面引起向上的感热通量，然后加热近地面层空气，形成对流，使边界层得到发展[51]，可见偏离度法、干绝热曲线法确定的HBL与地表温度、气温的相关性均较好，且两方法的HBL与气温的相关系数总体上高于与地表温度的相关系数，即符合太阳辐射—地表温度—气温—HBL的响应关系和响应次序，而国标法确定的HBL与地表温度、气温的相关性均较差，未能反映这一响应。

2.3.2HBL与气温、地表温度、风速的时间响应关系

由图7中25 d的07—19时逐小时平均值变化来看，日地表温度最高值出现在13时，日气温最高值则延迟2 h至15时出现，偏离度法确定的日最大HBL也是出现在15时，即平均状态下，日最大HBL对最高气温的响应时间在1 h左右，而对最高地表温度的响应时间为2 h左右，这符合大气边界层理论中关于太阳辐射—地表温度—气温—HBL的响应关系和次序[25,51-54]。由图8中25 d逐日出现时间来看，日最高地表温度在11—15时均有出现且较为集中，最多出现在13时(占比48.0%)；日最高气温在12—17时均有出现，最多出现在15时(占比48.0%)；偏离度法日最大HBL在13—16时均有出现且较为集中，最多也出现在15时(占比52.0%)，即自统计概率角度分析也显示这一响应。但是，国标法确定的平均状态下日最大HBL出现在16时(图7)，逐日的日最大HBL在09—17时均有出现且较为分散(图8)，最多出现在16时(占比24.0%)，受近地面风速和稳定度等级影响大、午后13—15时的坍塌是导致国标法日最大HBL出现时间偏差较大的主要原因，即国标法不能准确反映地表温度—气温—HBL的响应关系和次序。

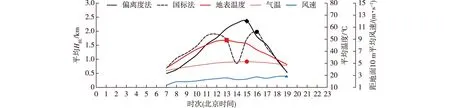
图7 济南2014年6—7月25 d平均的逐小时HBL与各气象条件演变对比Fig.7 Comparison of the evolution of the average hourly HBL and various meteorological conditions in Jinan in 25 d from June to July 2014

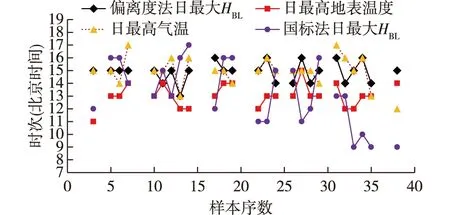
图8 济南2014年6—7月25 d的逐日最大HBL、最高地表温度、最高气温出现时间对比Fig.8 Comparison of the occurrence time of the daily maximum HBL, maximum surface temperature, and maximum air temperature in Jinan in 25 d from June to July 2014

平均状态下的距地面10 m高度的风速最大值出现在19时(图7)，显然偏离度法和国标法确定的HBL与平均风速的响应关系和次序均不明显。

2.4 两种方法确定的HBL与污染物浓度的关系

图9 济南2014年7月18日07—19时逐小时HBL与各污染物浓度变化对比Fig.9 Comparison of changes in the hourly HBL and pollutant concentrations in Jinan from 07:00 to 19:00 on 18 July 2014

另外，近地面各污染物质量浓度的最低值均出现在14时，而偏离度法最大HBL出现在15—16时，相差1～2 h，即两者并非同步负相关，这对于空气质量模型的改进十分关键。分析原因，应是与前述的对流边界层发展机制和各要素响应次序有关，近地面热浮力和动力抬升造成的湍流运动最强应是在14时前后，近地面污染物的扩散和稀释显然受此影响更大一些；而持续向上传递的热通量滞后造成最大HBL的出现时间延迟。

3 讨论与小结

基于上述结果的对比分析，结合三种方法的原理和相关文献研究资料，对比评估结果见表1。

表1 确定日最大HBL的三种方法综合对比评估

1)偏离度法突出的优点是：a)Cn2观测数据量大且时间分辨率高，可实现逐6 min的实时HBL确定；b)囿于Cn2就是表征湍流变化强弱的一个参数[36]，因此依据其廓线在边界层顶的突变或跃变特征确定出的HBL结果准确度较高，原理上优于其他两种方法；c)能判断给出HBL出现的具体时间，且可给出时空演变，确定的HBL符合对流边界层发展的规律，从而可为边界层精细化结构和演变特征的研究、应用，提供很好的实测和验证基础。但该方法也有缺陷：a)观测数据的空间垂直分辨率不如其他两种方法的高，导致确定的HBL在高度上的精度尚偏低；b)Cn2观测数据质量需严格控制，这是制约HBL确定的关键因素，最大程度地剔除杂波干扰、修正异常数据是亟待解决的问题；c)降水或多高度层的湿度大于85%情形下该方法并不适用，且该判别需借助于地面和探空观测资料，应用尚有局限；d)属于单一指标判断法，基于WPR观测的Cn2、信噪比(SNR)、速度谱宽、垂直径向速度等产品数据的综合指标判定HBL，可进一步提高准确度并实现自动判别[11,28,42-43]。

2)干绝热曲线法的优点是：a)L波段雷达探空数据的高度层分辨率高，可达10 m级，得到的HBL准确度较高；b)仅需要探空温度资料和地面日最高气温，资料易得且方法简易可操作，易于应用与推广；c)结果与方法一差异不大，相关性较好，证实确定结果较为接近实际的HBL[52]。但缺陷也很突出：a)该方法是基于将大气边界层内热力结构的显著变化仅仅归结为地面上热量输入重新分配的结果，而不考虑动力的作用[8]，07：15后只考虑了热力湍流的影响，而忽略平流、下沉以及机械湍流等的影响，因此晴天时HBL估算的精确度较高，而阴天时HBL估算的精确度较差[20,52]；b)L波段雷达探空站数量很少，远不能满足应用需求；c)只能直接估算日最大HBL，不能确定HBL出现的具体时间，也不能给出HBL的时空演变，已不能满足日益精细化边界层结构研究和应用需求。

3)国标法的优点是：地面气象台站多、资料易于获取、计算简便。但缺陷很突出：a)能给出HBL出现时间但存在较大偏差，可给出HBL时空演变但午后峰值偏差大，存在坍塌现象，确定的HBL不符合对流边界层演变规律，尤其在午后13—15时偏差更显著，实时准确度低；b)囿于是基于多年均值的风向、风速、稳定度联合概率分布推导的[17]，原理上该方法只适用于平均状况下的HBL确定，对于实时HBL的确定，适用性不好；c)仅依据地面观测数据判断高空1～4 km的大气湍流状况，导致与实际对流边界层的演变存在较大偏差；d)属于半经验公式，适用于定常边界层，对U10>6 m·s-1的非定常天气过程不适用[17]。

4)偏离度法确定的济南夏季25 d日最大HBL的平均值为2 500.0 m；逐小时HBL演变是波浪起伏式的，07—15时HBL缓慢增高、15时后有一些HBL是断崖式降低的；日最大HBL对最高气温、最高地表温度的平均响应时间分别为1、2 h左右；HBL逐小时值与各污染物质量浓度的相关性更好，但两者并非同步负相关。这可为研究边界层精细化结构，提高空气质量预报和大气自净能力判定的准确率等提供更好的参考。

5)冬季大气层结稳定、空气污染的程度较重，日最大HBL是人们更为关心的，但目前L波段雷达探空加密观测业务是在夏季三个月，建议冬季也应进行观测；并应结合WPR、激光雷达、微波辐射计等的观测资料，探索确定边界层精细化结构的更好方法，以不断推进理论研究及业务应用。