基于遗憾最小化算法的谣言抑制与演化博弈模型*

臧正功，丁 箐

(中国科学技术大学 软件学院，安徽 合肥230051)

0 引言

谣言是指未经验证或者篡改真实的信息[1]，随着通信网络的快速发展、即时通信和新兴互联网技术的应用，谣言传播在速度和广度远超历史任何时代。恶意谣言可能造成远超以往的大范围恐慌和严重经济损失[2]，对信息扩散过程与谣言抑制的研究成为社交网络的研究重点。

由于谣言扩散过程类似于疾病传播机制，经典的易感染去除模型SIR被借鉴和改进，文献[3]基于改进的八态ICSAR模型(无知者，信息载体，信息传播者，拥护者，撤离者)，建立了一个针对谣言传播的动态时空综合风险评估模型。文献[4]建立了具有动态友谊的随机异构网络SHIR模型，将社交网络中最常见的友情变化现象纳入其中。

与病毒感染不同，真实谣言传播依赖于社交网络中人的交互，而基于传染病模型的研究忽略了人在散布谣言中的自主作用。与疾病传播相反，个人在谣言传播过程中实际是自我决策问题。如何有效利用个体策略，抑制谣言传播成为研究的主要目的。疫苗接种理论[5]被引入到实际运用中。文献[6]尝试使用个人或者权威机构发送反谣言信息来抑制谣言。此外谣言抑制还取决于接受者与传播者的特征、亲密关系、谣言强度等因素[7]。

博弈论作为分析用户决策与竞争现象的典型数学工具被广泛应用于谣言抑制。文献[8]提出一种演化博弈模型来分析谣言过程，该模型考虑了用户的多维属性，并量化了外部和内部驱动因素对群体状态转变的影响。文献[9]通过将社交网络中的谣言传播建模为一种协作博弈，发现具有无标度属性网络可以更容易地促进谣言传播。传统的博弈论条件依赖度无限大，混合人口的假设，通过微分方程研究整体演化的动态过程[8-10]。但现实社交网络中面对有限、非理性个体时，如何对社交网图结构中舆情控制提出有效建模成为重点。针对网络结构和扩散动力学的研究有助于更好地理解网络的演化机制，因此本文引入图进化博弈理论[11]来研究网络结构策略的演化。

社交网络中当非理性对手不再使用纳什均衡策略博弈时，此时纳什均衡策略并不保证是最佳反应。为满足实时博弈中对策略的完善，利用对手弱点往往能取得更高回报，故提出从自我遗憾最小化角度建模[12]。其思想是从遗憾最小化的角度来利用次优对手弱点，并基于一种离线的均衡计算，从个体自身选择的经验中学习更新策略。文献[13]探讨了政府的惩罚和个人的敏感性如何影响谣言的演变。由此可见，网络结构、谣言强度、用户策略以及谣言控制中心存在与否都影响着其传播。

本文在图论的基础上采用演化博弈概念，引入遗憾最小化算法来研究网络中谣言抑制与用户策略的演化。本文的贡献可归纳为：(1)结合图演化博弈论，考虑个体特征与社交网络规则图结构，提出了新型演化博弈模型；(2)利用次优对手弱点，提出遗憾最小化算法实现个体更新策略。

1 模型构建

本节介绍了用于谣言控制的进化博弈模型的构建。首先设计博弈模型的收益矩阵，然后计算策略更新的复制动力方程，最后获得演化稳定状态的条件。

1.1 演化模型描述

本文讨论谣言和权威信息同时在复杂的社交网络中传播。假设当个人传播一条信息时，他或她的所有朋友都可以阅读。用户有三种可能的动作：谣言传播、反谣言传播以及忽略谣言或反谣言。反谣言是说服人们谣言不真实的信息。因此，此处考虑三种策略：谣言传播(RS)、反谣言传播(ARS)和无知(I)。

网络建模为图 G=(V，E，A，P，U)，其中 V 为节点集；E是边关系集；A表示节点的行为集，节点的交互行为与其采用策略有关；P是随机事件概率函数；U是节点的效用函数。本文所用的参数定义如表1所示。

表1 参数定义

通常用户对谣言或者反谣言的兴趣取决于其对信息内容的认知，本文参照文献[3]将其设定为固定参数；而谣言与反谣言强度意味着能促使舆情扩散的力度，本文依据文献[6]谣言传播强度SR取决于谣言主题的严重性与歧义性，反谣言强度SAR取决于反谣言机构的权威性与证据真实性。同时政府等权威机构发布反谣言新的概率为RC：当谣言传播人数NRS超过风险人数阈值Q=βN时，政府将开始传播反谣言，其中0＜β＜1，为风险系数，谣言控制中心对所有传播谣言的节点实施成本为PUN的惩罚。

为简单起见，将支付矩阵的参数组合为3个变量：UR，UAR，UI，如下所示：

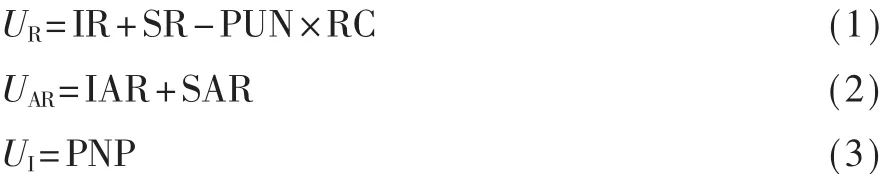
设定回报收益已归一化(0，1)间，收益的物理含义是可能取得的回报。例如当具有策略RS的用户A与具有策略I的用户B相遇时，B会以的比率成为RS，n为策略个数。相同策略的用户交互收益为 0。

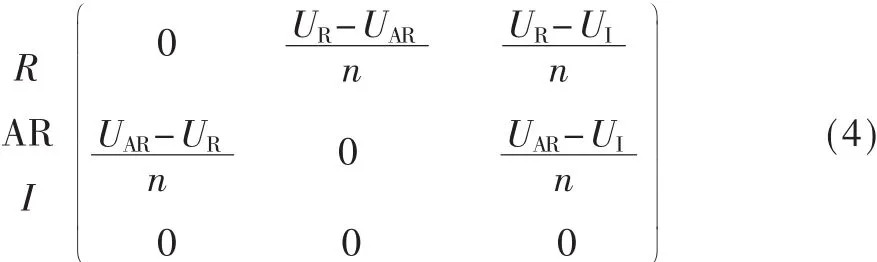
式(4)表示博弈模型的收益矩阵。在完整图博弈中，所有个体都相邻，根据与所有相邻个体的交互来局部确定个体的适应性。文献[11]考虑进化动力学更新规则(IM)，其代表用户策略频率随时间变化的方式。本文考虑网络中静态结构，不涉及网络单个节点的消亡。针对IM规则，定义动态微分方程来描述图表上每个人的期望频率随时间的变化，见式(5)。考虑n个进化策略，总收益矩阵A=[aij]。同时更新机制定义了 n×n矩阵 B=[bij]，如下在度为 k的无限大图中：

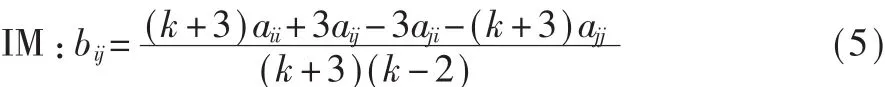
其中，aij表示策略i对抗策略 j的收益。收益博弈动力学从充分混合群(完整图)移动到度为k的规则图上，可以近似通过回报矩阵的转换来描述：

这里 A=[aij]，B=[bij]，等式(6)解释了两 个矩 阵之间的变换。实验论证与事实表明[11]，对于非规则图，博弈从充分混合的总体移至规则图形只导致收益矩阵的转换。因此，新的收益矩阵是原始收益矩阵加上另一个矩阵的总和。

转换后的收益矩阵[aij+bij]可通过式(9)获得：

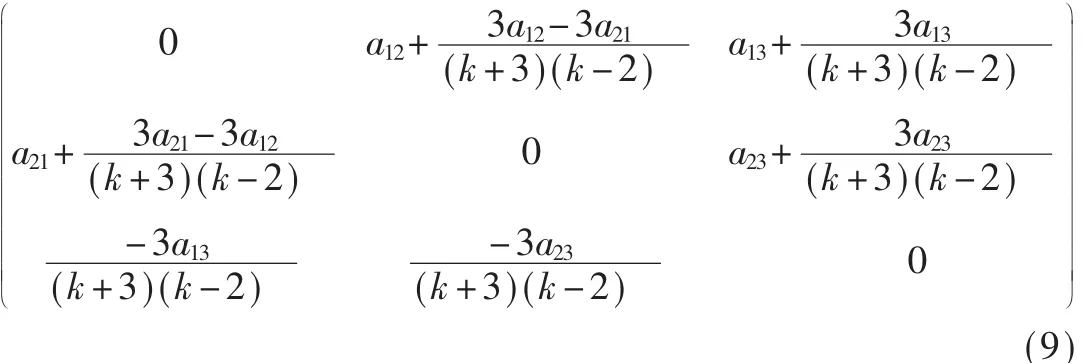
1.2 遗憾最小化算法策略更新规则

博弈过程中的遗憾是指通过对过去博弈中动作的遗憾程度来预测未来动作选择，定义σi为用户i所使用的策略，博弈中除i以外的参与者策略为σ-i，则对 σi的最佳响应策略有：

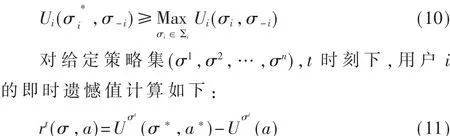
其含义为用户在第t轮依据策略执行动作a，与相对按照最佳响应策略σ*采取动作效用值之差。若该值为正，则说明用户应较多地执行动作a*，否则会产生遗憾。因此用户i的T轮累积遗憾值为：

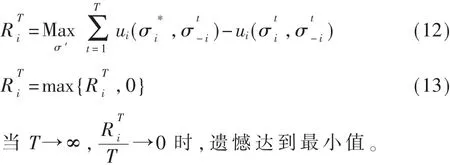
在迭代过程中玩家对动作集进行分配时，即时遗憾值将用来进行下一轮的迭代策略更新，通过不同动作的积极遗憾值匹配，使得遗憾向均衡收敛。故T+1轮迭代中，用户i根据概率选择动作a∈A，有：

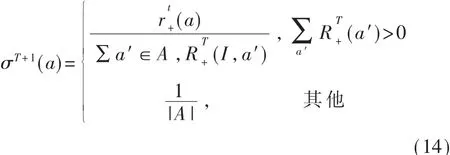
动态估计法则对新产生的博弈结果赋予更高的权重，使遗憾价值更能够体现对手策略的动态变化。详细过程见算法1。

算法1折扣遗憾最小化的在线算法

输出：σT+1(a)

(1)for每一轮博弈

(2)按照 σi与对手进行博弈

(3)记录博弈收益U，并计算出即时遗憾价值 r；

(4)对每一个动作进行虚拟遗憾价值的更新R，并计算不同策略占比，更新其策略；

(5)end for

1.3 进化稳定策略证明

如果策略ARS执行概率占比高于其他策略[14]，即 PARS＞PRS且 PARS＞PI，则 ARS 为进化稳定策略(ESS)。具体分析如下：假设 A→B，根据文献[14]依次可得：

2 博弈模型仿真结果与分析

2.1 数据描述

本文使用了两种真实的社交网络数据集，如表2所示。第一个是Blog数据集，该数据集包含该社交博客目录网站的友谊关系以及成员身份。第二个是电子邮件数据集(DNC emails)。网络中的节点对应于数据集中的人员。数据集均符合典型幂律度分布。

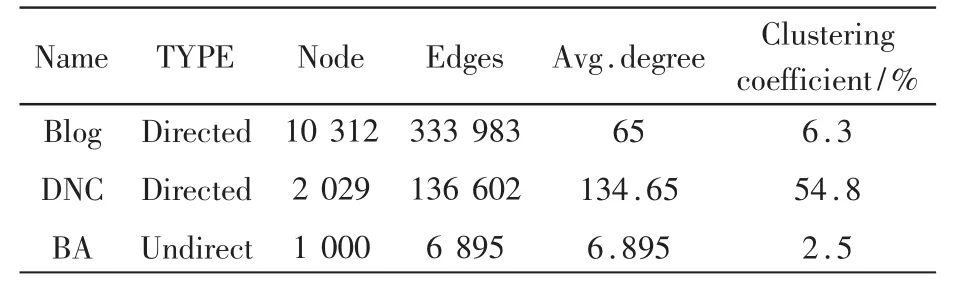
表2 网络参数

本节尝试通过对不同的仿真来分析所提出的模型。首先，针对三种策略和ESS条件计算复制器动力学，并在图中进行了说明，以进行参数样本评估。其次，基于数据集的两个真实世界图进行谣言传播实验,以验证复制动力学的进化稳定状态。

2.2 复制动态方程

本文研究中，推导出了式(15)、(16)、(17)，对于变量的样本配置，此处列出样本初始收益矩阵参数：IR=0.2，SR=0.2，IAR=0.3，SAR=0.3，PUN=0.1，PNP=0.25，β=0.1，折扣因子 λ=0.9。

设置初始策略比例为：RS=0.25，ARS=0.05，I=0.70。根据等式中给出的演化稳定策略的初始值有：满足ARS为 ESS的前提。

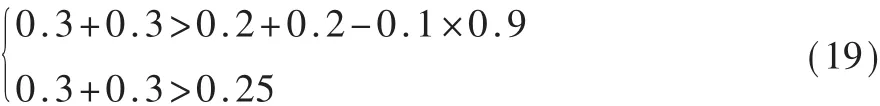
2.3 基于不同图的模型仿真

(1)BA图模型进行数值模拟

研究表明现实社交网络通常都具有无标度特性，因此使用BA图模型进行数值模拟。

图1展示状态RS、ARS和I策略节点在Barabasi-Albert无标度网络上随迭代时间变化的扩散过程，并通过模拟进化更新规则得出仿真结果。实验对生成的1 000个节点采取不同策略进行随机初始化，其收益矩阵参数初始化等同上节复制动力学的样本参数。从图1可见，BA网络的演化博弈模型仿真结果与数值推理一致，并且ARS策略为演化稳定状态。

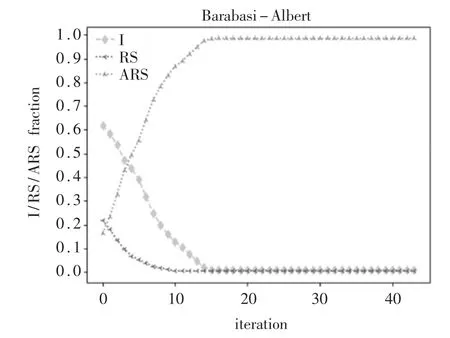
图1 谣言、反谣言、无知者在BA图模拟比例

(2)真实社交图仿真

本节按照比例初始化三种状态的用户节点，支付矩阵的初始化参照于样本参数。

图 2中(a)与(b)分别显示 Blog和 DNC两种真实社交图上的仿真结果。其中图(a)最终ARS态节点比例较图(b)高，且网络中易感节点占比远低于图(b)，但二者稳态时ARS比例均低于图(1)中BA图。

与BA图模拟结果的差异来自于真实图形结构差异化。例如参考到DNC图的平均聚类系数为54.8%，比BA图聚类系数2.5%较大，这是因为DNC中包含较多自我中心网络(ego network)，并且处于不同自我中心网络的用户彼此间访问受限[15]，因此策略难以传播到整个网络节点。但仍可以在真实社交网络图的仿真结果与复制动态方程间找到一致性。而聚类系数较小的Blog图与DNC相比最终治愈者比例更高，更快收敛至进化稳定状态。从图(a)与图(b)的快照中可以看出，ARS策略是进化稳定状态，即在真实图形上的仿真结果与复制器方程之间存在相当好的一致性。这个结果意味着可以使用该演化博弈的复制方程来对社交网络进行进化博弈分析。

(3)不同模型过程对比

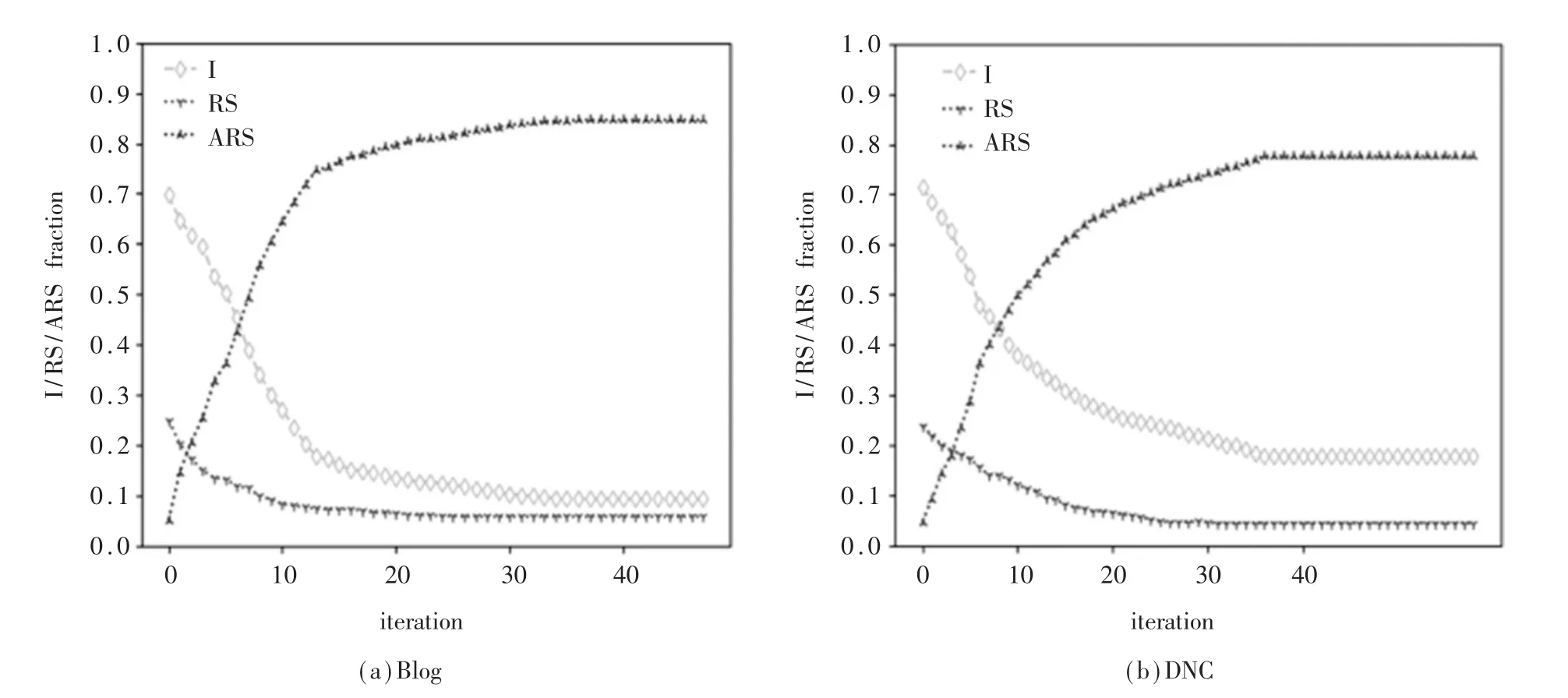
图2 谣言、反谣言、无知者在Blog与DNC真实网络图的模拟结果

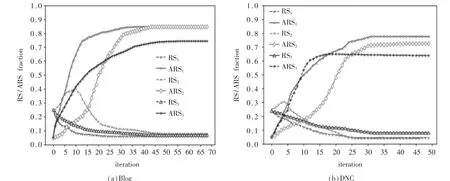
图3 三种不同模型下谣言、反谣言者在Blog和DNC模拟过程

图3 表示不同社交网络中，本文模型与文献[4]、[8]两类演化博弈模型间关于谣言者、反谣言者的模拟过程。其中第一组为本文所提模型；第二组为SHIR[4]，该模型充分考虑反谣言和用户心理因素，运用进化博弈论和多元信息回归方法来构建信息传播进化模型；第三组为 RDG模型[8]，该模型假设个人根据不同的亲密强度选择邻居之一进行策略模仿，探究惩罚成本与邻居策略对舆情扩散的影响。

实验结果显示，第二组模型中谣言者RS会在短暂上升后逐渐下降，最终趋向稳态，而其ARS策略趋向稳态时占比与第一组模型相似，但所需时间较长。这是因为第二组模型中SHIR分别代表易感、已知、感染、恢复四种状态，网络中感染节点I会在传播初期感染大量易感节点S后，才会产生已知节点K来进行反谣言的对抗，从而导致初期RS占比的短暂提升。第三组模型较第一、二组网络中ARS占比较低，其原因在于在相同惩罚成本的情况下，用户盲目选择邻居策略较多导致整体谣言抑制效果较弱。

图4绘制了两个社交网络中不同风险阈值比率和治愈者与传播者平均最终数量，为更好地理解结果，定义反谣言传播者支配措施NARSDM=值得注意的是，当网络中风险阈值较小时，即存在少量谣言传播者也将受到惩罚，此时谣言传播覆盖面较小，NARSDM较大，随着风险阈值的扩大，网络中谣言覆盖面变大，NARSDM变小，即风险阈值β与NARSDM成负相关。风险阈值增大意味着更多的谣言传播者将面临被惩罚的负担，从而使得策略更新时，选择反谣言的遗憾值更大,从而更多用户选择传播ARS。从图4可以看出，当风险阈值从0.2降至0.1时，网络中最终存在的治愈者比例并没有大幅度提高。

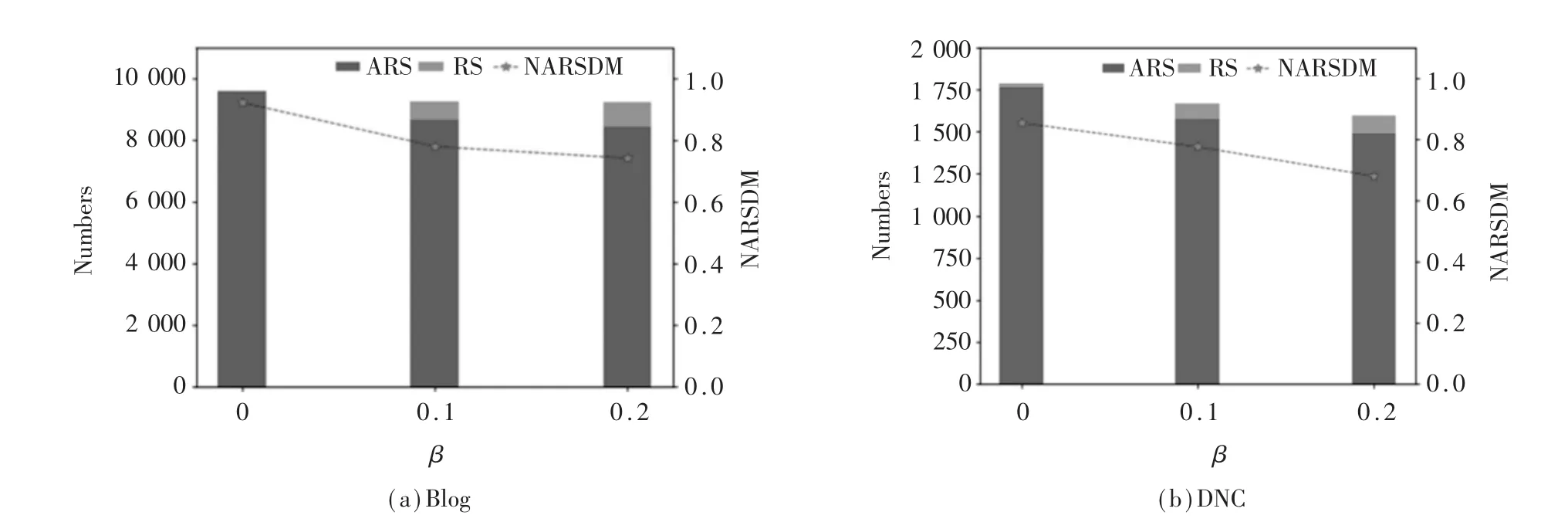
图4 不同谣言策略与风险系数β所对应的NARSDM和最终数量

3 结束语

本文提出一种图演化博弈模型用于分析社交图谱上用户决策与谣言扩散过程。首先针对完整图规则与现实网拓扑差异，在图论的基础上采用演化博弈，设置策略更新规则中采取遗憾匹配与动态折扣，同时通过定义反谣言传播者支配措施NARSDM衡量网络中风险阈值比例与状态节点数量关系。实验部分首先在无标度图BA上进行数值模拟，节点采取不同策略初始化，结果表明ARS策略为ESS状态。然后在两真实世界图进行仿真，仿真结果表明真实世界图中进化稳态状态与复制动态方程具有一致性。