基于博弈论的总承包商分包管理优势策略研究

张昶

【摘 要】本文主要基于非合作博弈“囚徒困境”对大家都不利的“纳什均衡”原理，通过对总承包商分包管理策略研究，探讨避免博弈中陷入“囚徒困境”的策略，提出施工企业总承包商应建立一个总承包商和分包商都积极遵守的长效合作机制，采取优势策略开展合作博弈能使双方获得满意收益，最终实现共赢目标。

【关键词】非合作博弈;合作博弈;优势策略

【Abstract】Based on the"Nash equilibrium" principle of non-cooperative game "prisoner's dilemma"， this paper discusses how to avoid to the "prisoner's dilemma" in game strategy through to the general contractor subcontract management strategy research. Then put forward to the long-term cooperation mechanism which general contracto and subcontractors should actively comply with.At last， we should take advantage of dominant strategy to ultimately achieve a win-win goal.

【Key words】Non-cooperative game;Cooperative game;Dominant strategy

1. 引言

（1）建筑市场施工环节中的总承包商与分包商之间经常矛盾重重，纠纷不断，致使项目质量下降，工期拖延时有发生。如何处理好总包与分包管理方式，促进建筑市场有序健康发展已经成为人们的研究课题。

（2）博弈论在经济管理中已经得到广泛应用，研究表明施工企业总承包商和分包商在工程项目实施中作为相对独立的利益团体，其利益目标不可能完全一致，双方之间存在明显的博弈关系[1～2]。“囚徒困境”是博弈论中非合作博弈最为经典的博弈模型，通过“囚徒困境”原理，我们看到，假如每个人都从利已的角度出发，最后的结果竟然是对大家都不利的“纳什均衡”，个人的理性导致的竟然是集体的非理性，是非合作的博弈均衡，而合作则是好的走出“囚徒困境”的利己策略。“囚徒困境”深刻地反应了社会中人与人的一种博弈状态，从博弈论的角度来说有限次的博弈双方是没有兴趣进行合作的，如果博弈多次重复，合作就可能出现，均衡结果可能与一次博弈大不相同[3～7]。

（3）本文立足于合作博弈可能得到共赢局面，探讨走出共输达到共赢对应的劣势与优势策略组合取舍，找到使双方获得满意收益，即共赢的优势策略。同时借鉴现行的一些项目管理理论对当前企业总承包商与分包商之间存在的问题和解决方法进行一定的研究。

2. “囚徒困境”博弈模型

（1）假设有两个小偷T和J共同犯案、私入民宅被警察抓住。警方将两人隔离审讯，对每一个犯罪嫌疑人，警方给出的政策是：如果一个犯罪嫌疑人坦白了罪行，交出了赃物，于是证据确凿，两人都被判有罪;如果另一个犯罪嫌疑人也作了坦白，则两人各被判刑8年;如果另一个犯罪嫌人没有坦白而是抵赖，则以妨碍公务罪（因已有证据表明其有罪）再加刑2年，而坦白者有功被减刑8年，立即释放。如果两人都抵赖，则警方因证据不足不能判两人的偷窃罪，但可以私入民宅的罪名将两人各判入狱1年。

（2）用博弈论术语来说，T或J可以做出的选择被称为“策略”，如“坦白”或者“抵赖”都是策略行为，对T来说尽管他不知道道J是选择了“坦白”还是“抵赖”，他认为他自己选择“坦白”还是比选择“抵赖”好些。也就是说“抵赖”是相对于“坦白”的劣势策略，T不会选择劣势策略，他一般会选择“坦白”的优势策略。对J来说也会动这样的脑筋，最终，两个人都选择了坦白，结果都被判8年刑期。

（3）在这个案例中，T和J所选择的策略组合（坦白，坦白）和（抵赖，抵赖）都能实现博弈均衡。这个策略组合存在优劣之分，前者是优势策略，后者是劣势策略，但T和J一般都不会选择对大家有利的劣势策略“抵赖”，也就是“坦白”是优于“抵赖”的好的策略。类似的这种博弈均衡是1994年诺贝尔经济学奖得主纳什论证的，所以被称为“纳什均衡”，这是一种非合作博弈均衡，并不是对所有人都有利的均衡。

3. 总包与分包的博弈模型

（1）在本节的博弈里，有两个参与人：总承包商和分包商。其中总承包商的策略是：第一种是按照国家规定，保证分包商具有一定的利润空间，及时拨付工程款，设为A1;另一种是降低分包商的利润空间，将工程价格尽可能的压到最低，并延期付款，设为A2。分包商的策略有两种：第一种是信守合同，保证质量和工期，设为B1;另一种是合同违约，设为B2。

（2）设Q为符合合同要求的合格工程; UQ为不符合合同要求的不合格工程;P为工程款; E1为总承包商挤压分包商利润获得的收益和延期付款节省的财务费用;E2为分包商的适度利润和及时得到工程款而减少的财务费用;C表示分包商为了短期利益而节约的成本（在采取减少必要的劳力投入或材料、设备投入行为的情况下），不包括分包商在保证工程正常施工情况下运用科学的管理方法节约的费用。

参与人双方的支付矩阵为（表2） 。

（3）由支付矩阵可以看出： 无论总承包商选择A1及时付款还是A2延期付款，分包商在沒有其它约束情况下的最优策略为B2合同违约;无论分包商选择信守合同，还是合同违约，在没有其它约束的情况下，总承包商的最优策略为A2延期付款。博弈的纳什均衡为：（ A2，B2），这个纳什均衡对于博弈的某一方来说是理性的选择，但是对于集体来说是一个最不利的结果，总承包商和分包商陷入了“囚徒困境”。

4. 避免博弈中陷入“囚徒困境”的策略

进入“囚徒困境”对总承包商和分包商都没有好处，从博弈论的角度看，出现“囚徒困境”的主要原因是双方不合作。在工程实际中，为了改变这种状况，就需要对博弈过程和规则进行一定的改变，使非合作博弈转化为合作博弈，最后博弈结果能够达到最优或次优。

4.1 增加影响制约因素调整支付矩阵。

（1）在实际工程中，建立健全有关规章制度，加强建设项目过程中的监控机制，强化违约处罚，迫使总承包商、分包商的行为自律，同时总包做好对分包商的服务工作，具有积极引导分包商作出理智决策的作用，从而走向合作。如在分包领域强制性地建立完备的工程担保和保险制度，双方各自出具的合同履行担保会极大地促进双方积极履行合同。

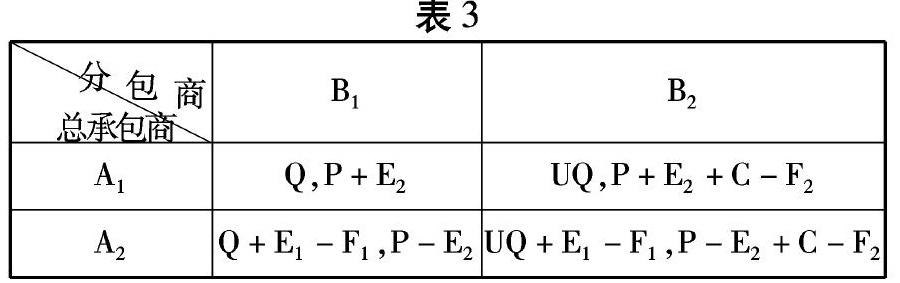
博弈中在加入了工程违约罚金的支付矩阵（表3） 。

（2）从支付矩阵中可以看出，当总承包商的违约罚金在一个合理的水平时，挤压分包商利润获得的收益和延期付款节省的财务费用E1与违约罚金F1的差值将是负值，总承包商策略A2延期付款将会得不偿失。同理，分包商的违约罚金也调节了分包商的收益，使分包商信守合同的收益大于合同违约的收益。在这种收益状况下，博弈的均衡就会是：（A1，B1） ，这是对双方有利的优势策略组合。

4.2 长期合作多次博弈。

（1）以上讨论的是总承包商同分包商的一次博弈，双方考虑的只是一次博弈过程中的最优利益。如果博弈模型为多次博弈，博弈方考虑的将会不仅仅是短期的利益，长期利益将会是考虑的重点。

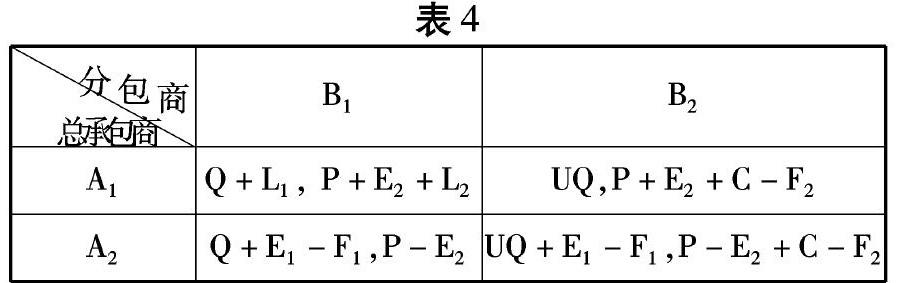
博弈中加入双方长期收益情况下的支付矩阵（表4） 。

（2）从支付矩阵可看出，当总承包商诚信履约，保证分包商适度利润并及时付款获得的长期收益大于挤压分包商利润获得的收益和延期付款节省的财务费用时，即L1≥I1，总承包商策略A2将不再是最优选择。同理，当分包商信守合同并积极施工获得长期收益大于分包商为了短期利益节约的成本时，即L2≥C，分包商为了获得更加可观的长期收益将不再采取减少投入，甚至偷工减料的成本节约措施。在这种收益状况下，博弈的均衡就将是（A1，B1），这是对双方有利的优势策略组合。可见当长期收益更为重要的时候，长期的收益将会成为博弈决策的决定因素。

5. 结论

施工企业总承包商是在分包过程中占主导地位，拥有大量的分包商，其分包管理策略对项目最终收益有重要影响，非合作博弈会导致总承包商和分包商在个体理性下，分包商会选择合同违约、不积极施工，总承包商会选择挤压分包商利润并延期付款，双方陷入“囚徒困境”。 这就需要在博弈过程中加入有利的影响制约因素，改变双方的支付矩阵，如建立健全建设项目过程中的监控机制，强化违约处罚，迫使双方行为自律，而做好总包管理服务工作，具有积极引导分包商作出理智决策的作用，最终促进双方积极履行合同。而建立合作伙伴机制创造多次博弈的情况下，无论是总承包商还是分包商都将会严守信用，在决策的过程中，不会只看重眼前的利益，而会为了以后的发展选择更为理智的决策，为此必须建立总承包商和分包商的长效合作机制，双方由合同关系转变为合伙关系，采取优势策略开展合作博弈能使双方获得满意收益，最终实现共赢目标。

参考文献

[1] 王家辉.博弈论中的“囚徒困境”模型[J].《统计与决策》，2005（15）.

[2] 方芳，杨琦峰.张斯航.工程项目管理中的“囚徒困境”博弈研究[J].《当代经济》，2008（12） .

[3] 毕春丽  陈鹏  王长峰.企业工程项目总承包商与分包商博弈模型与策略研究[J].《项目管理技术》 2010（5） .

[4] 朱高明，王喜军，王孟均.博弈论在工程管理中的应用 [J].长沙铁道学院学报，2002，（1）.

[5] 刘振奎.博弈论在工程项目冲突管理中的应用[J] .《基建优化》2007（6）.

[6] 謝识予.经济博弈论[M].上海：复旦大学出版社.2002.

[7] 杨晓林. 建设项目总承包商与分包商合作关系的单期博弈分析[J].《工程管理学报》. 2010（5） .