线弹性断裂力学问题的扩展自然单元法

陈莘莘，刁呈岩，肖树聪

(华东交通大学土木建筑学院，江西，南昌 330013)

无网格法[1-3]可以克服传统的数值模拟方法对于单元或者网格的依赖性，不仅可以保证计算的精度，而且可以减小计算的难度。经过诸多学者的研究，目前发展的无网格方法主要有无单元Galerkin 法[4-5]、无网格局部Petrov-Galerkin 法[6-7]、边界无单元法[8]、重构核粒子法[9-10]、二阶一致无网格法[11-12]和自然单元法[13-14]等。其中，自然单元法在众多无网格法中展示了其突出的优点。自然单元法的近似函数满足插值性，可以方便地施加本质边界条件，并且形函数的计算不涉及矩阵求逆以及人为参数的选择问题。因此，自然单元法具有良好的发展前景，并且已经在许多领域得到了广泛的应用[15-19]。

虽然无网格法在处理裂纹问题上具有有限元等传统数值方法不可比拟的优越性，但仍然存在一些问题。为了较好地模拟裂纹尖端的应力奇异性，无网格法主要采用了修正裂纹附近的权函数、内部增强、外部增强以及单位分解增强等技术手段[20]。其中，单位分解增强法[21-22]的附加变量不多，并且计算精度较高。基于单位分解法思想，美国西北大学Mones 等[23]在有限元框架内提出了扩展有限元法(XFEM)，用以求解强和弱不连续问题。受XFEM 的启发，Ventura 等[24]基于单位分解法思想提出了扩展无网格法(XEFG)。Shi等[25]应用XEFG 法对不同长度和倾角的裂纹共存时的相互影响进行了研究。Rabczuk 和Zi[26]采用XEFG 法对准静态和动态粘性裂纹扩展问题进行了分析。针对XEFG 法处理本质边界条件比较困难的缺点，马文涛等[27]提出了扩展径向点插值无网格法(XRPIM)。此外，王峰等[28]将滑动Kriging插值法引入XEFG 法中，并将其用于含夹杂复合材料问题的求解。

鉴于自然单元法的优越性，本文在单位分解框架下提出了扩展自然单元法(extended natural element method, XNEM)，试图为线弹性断裂力学问题提供更为适用的数值分析方法。该方法在自然单元法的位移模式中加入阶跃函数和裂尖渐进位移场函数，并通过水平集方法(level set method, LSM)确定裂纹面和裂尖区域。典型的数值算例验证了本文方法的正确性和有效性。

1 扩展自然单元法不连续位移模式

1.1 自然邻接点插值

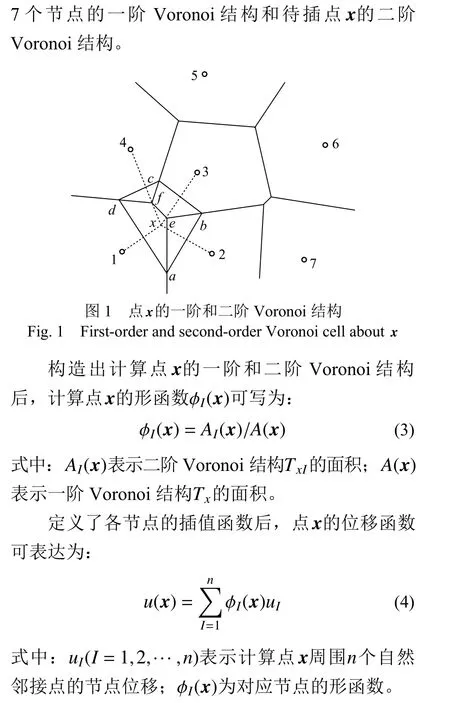
1.2 扩展自然单元法的位移模式

2 离散方程的导出

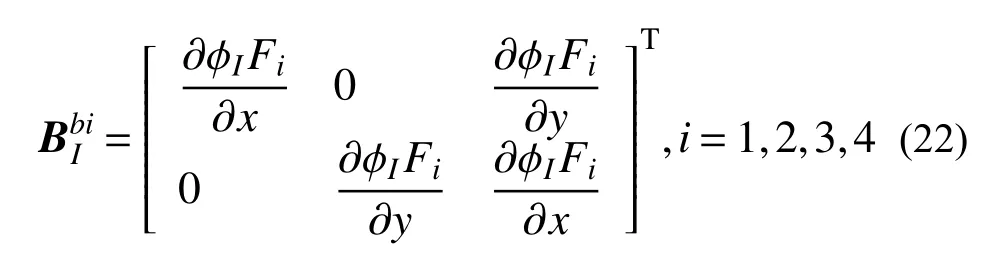
3 互作用积分法求解应力强度因子

4 数值算例

4.1 单边裂纹板受拉伸作用

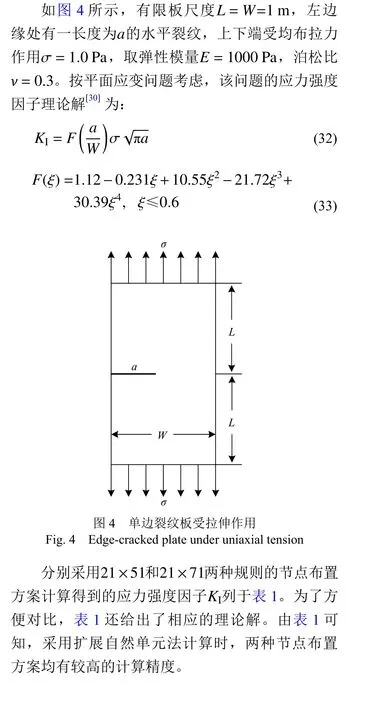
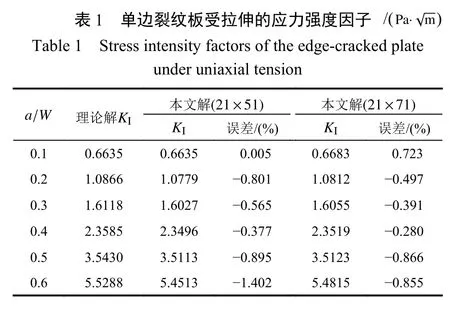
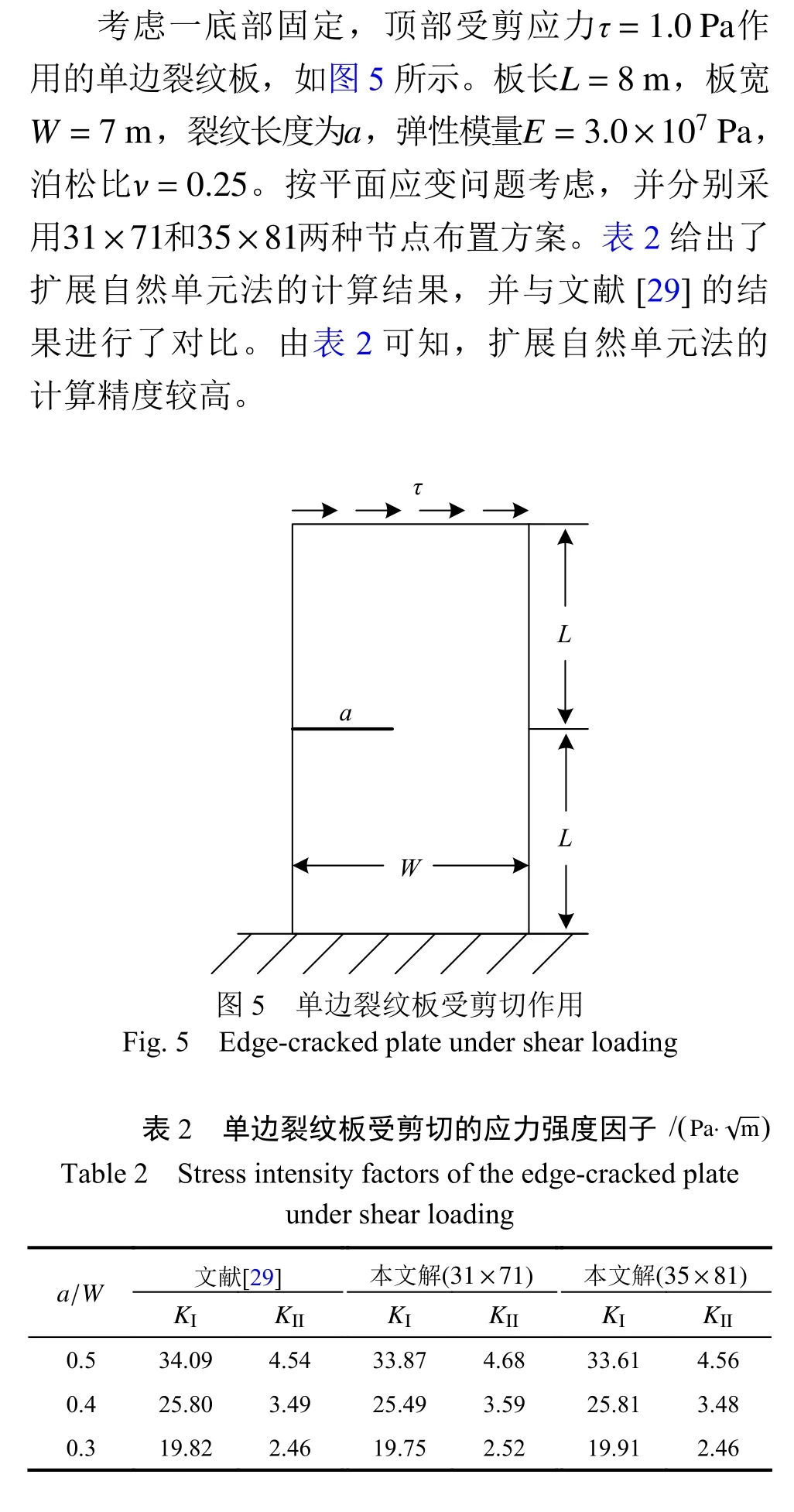
4.2 单边裂纹矩形板受剪切作用

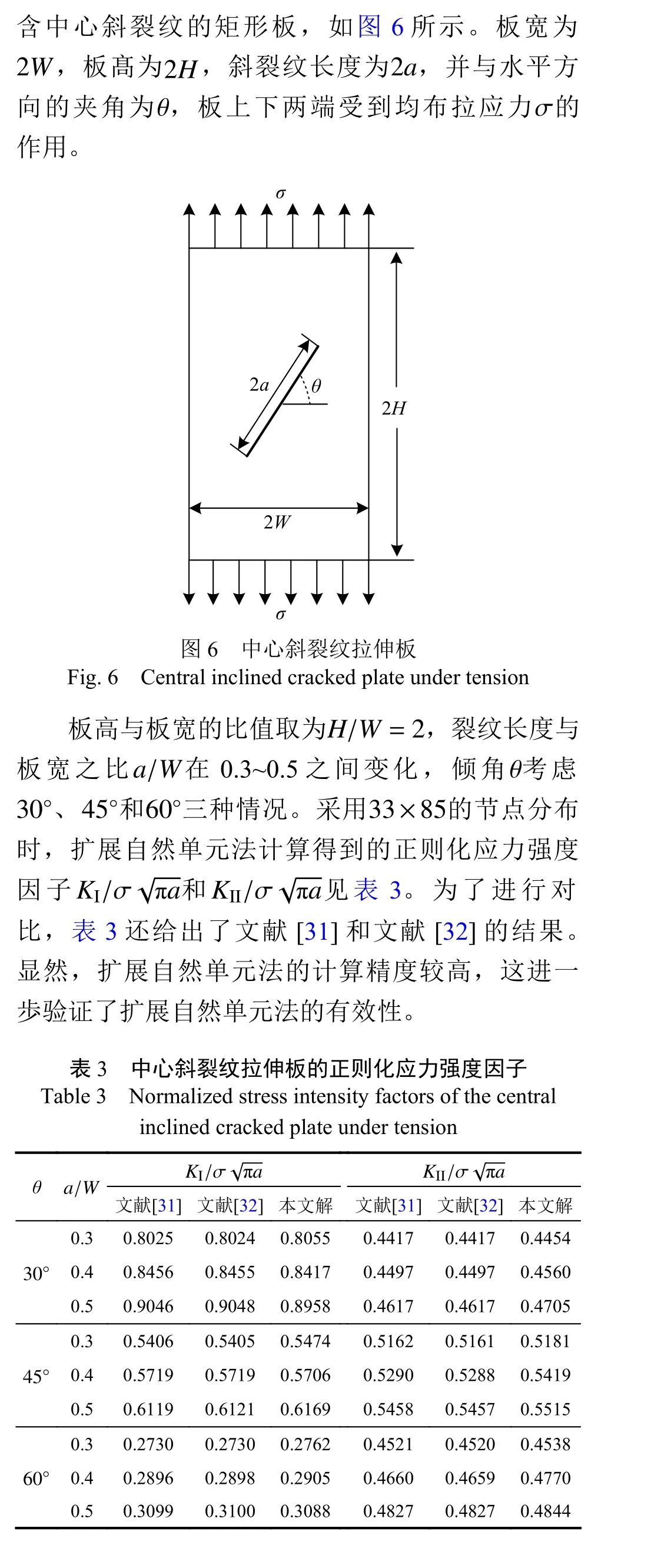
4.3 中心斜裂纹矩形板受拉力

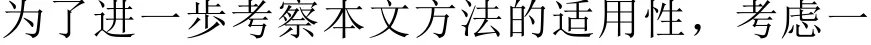
5 结论

自然单元法采用计算点的自然邻接点、Voronoi结构和无网格的方式构造整体求解的近似位移函数，不仅保证了计算精度而且简化了数值计算的前处理过程。需要特别指出的是，自然单元法的形函数不仅满足插值性，而且形函数的计算不涉及矩阵求逆，更没有人为参数的选择问题。基于单位分解思想，在自然单元法的位移模式中加入扩展项表征不连续位移场和裂纹尖端奇异场的基础上，本文首次提出了扩展自然单元法。算例分析表明，扩展自然单元法能够较好地求解线弹性断裂问题，具有较高的计算精度。由于近似函数满足插值性，扩展自然单元法较XEFG 可以更方便地施加本质边界条件。