集装箱港口多资源协同调度优化模型

高钰珊，陈 宁

（武汉理工大学 交通学院，湖北 武汉 430063）

1 引言

全球化的深度融合推动了国际贸易的快速增长，而集装箱吞吐量的不断突破对集装箱港口装卸作业的生产效率提出了新的要求。集装箱码头装卸作业系统作为复杂且环节丰富的主体，其单阶段的研究环境过于理想化、片面化，越来越多的学者开始研究码头调度的集成优化。

近年来三种以及以上的多资源、多环节的综合调度研究还不多见。主要研究对象是泊位、岸桥、集卡、场桥等资源，采用的智能算法多为遗传算法，但现有研究考虑的约束不太全面，且港口资源技术更新使得研究的基础数据需要进行新的定义。

本文针对码头核心作业资源的集成调度问题，将作业整体费用最少作为优化目标建立模型，并通过实例演算验证其可行性。本文优化目标在于通过建立优化泊位、岸桥与集卡的联合调度模型，达到港口总体成本的最小化，实现利益增收，对于船舶公司来说也能通过经济效益的提升带动港口城市区域建设与经济发展。

2 问题描述与假设

本文以Y港口作为调研对象进行研究，以72h为一个研究周期，在港口设施数目既定的条件下研究船舶的泊位分配和为该船配置合理的岸桥以及对每个作业的岸桥分配较优数量的集卡。

（1）到港船舶和泊位条件假设：①研究船舶属于动态到港情况，且每艘船舶到港时间等相关数据可以提前获知，其中船舶装卸任务量均以20ft的标准箱计量。②每艘船舶均有偏好靠泊位置，偏移时产生偏移成本；③不考虑平衡问题、水深问题、移泊问题；④不考虑拖轮对船舶进出泊位时间的影响。

（2）岸桥条件假设：①所有岸桥均在同一轨道上，两岸桥之间的安全距离为10m；②假设所有岸桥工作效率相同，不考虑岸桥维修、工人休息等因素对时间的影响；③岸桥作业时不可交叉跨越。

（3）集卡条件假设：①码头集卡数量一定，且只考虑内集卡；②所有集卡的成本相同，每辆集卡一次只能运输一个集装箱，不同位置集卡的最优路径花费时间不同；③不考虑集卡损坏与维修时间、司机休息时间，且不考虑其相关成本。

3 符号定义

下面提到的所有变量均是研究周期中产生的，原则上变量数值非负。

（1）常量：G-船舶集合；mg-到港船舶数，该数值是正整数；T-研究周期，本次研究定为72h，且时间单位精确到分钟；L-港口岸线的总长度；M-泊位集合；Q-港口岸线上岸桥集合；nq-岸线上岸桥的总数；R-港口岸线上集卡集合；nr-岸线上集卡的总数；Lg-船舶g的长度；bg-船舶g的到港时间；Eg-船舶g期望的离港时间，即船期；-船舶g最大岸桥配给需求量；-船舶g最小岸桥配给需求量；f1-设定船舶停靠安全距离为10m；f2-设定船舶进出时间间隔为10min；Pg-船舶g的偏好位置，Pg∈M；βg-船舶g入泊位置偏移偏好位置的单位偏移成本，单位：元/m；βr-任一集卡等待岸桥出现时的单位时间成本，单位：元/min；Wg-船舶g需要完成的装卸任务量；vt-岸桥每完成一个集装箱装卸工作花费的平均时间；trg-为船舶g服务的集卡从岸桥出发前往箱区到返回岸桥一次的平均作业时间；Cb-任一船舶在泊工作时的单位作业时间成本，单位：元/min；Cq-任一岸桥工作时的单位作业时间成本，单位：元/min；Cr-任一集卡进行运输工作时的单位作业时间成本，单位：元/min；-船舶g发生船期延误时，其出现的单位惩罚成本，单位：元/min。

（2）决策变量：srg-船舶g入泊的时间；Dg-船舶g最终靠泊位置；nqg-船舶g配给的岸桥实际数量；-船舶g被配给的岸桥q所分担的任务量；r-船g舶g配给的集卡数-为船舶g服务的岸桥q单独配给集卡数。

（3）从属变量：-在t时刻，岸桥q所在位置；eg-船舶g最终的实际离港时间；wtg-船舶自入泊到离港的实际在泊时间-为船舶g提供服务的岸桥q实际花费的作业时间；yg-船舶g的滞期时间；-船舶g对应岸桥q时，对应集卡等待岸桥作业的时间；-(0,1)变量，若船舶g在t时刻入泊，该判断值为1，反之为0；-(0,1)变量，若在t时刻岸桥q为船舶g服务时，对应判断值为1，反之为变量，当t时刻船舶g1，g2均处于在泊状态时，船舶g1停靠在船舶g2左侧时判断值为1，否则为0，g1，变量，当船舶g1，g2均需要停靠在岸线贝位d时，若船舶g1在船舶g2靠港之前靠泊，判断值为1，反之为（0,1）变量，在t时刻若船舶g对应的岸桥q下存在集卡 r进行工作则为 1，反之为 0，g∈G,q∈Q,t∈T,r∈R。

4 模型建立

建立的数学模型如下：

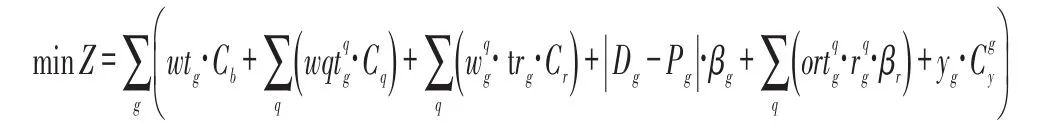
将研究周期内所有船舶在港的各项费用总和最少作为目标，函数内按从左到右的顺序依次表示船舶在泊费用、岸桥作业费用、集卡作业费用、偏移成本、集卡等待岸桥成本、船舶延期成本。

约束条件如下：

其中：式（1）约束船舶不移泊；式（2）、式（3）表示禁止船舶出现空间、时间重叠的约束；式（4）表示船舶长度约束；式（5）、式（6）约束岸桥配备数量符合实际约束；式（7）表示岸桥连续化约束；式（8）表示岸桥同时刻的唯一性服务约束；式（9）表示岸桥与船舶装卸量关系约束；式（10）、式（11）约束集卡配备符合实际限制；式（12）—式（15）分别对船舶在泊时间、岸桥工作时间、集卡等待岸桥时间以及船舶实际离港时间进行关系定义；式（16）表示船舶入泊时间的取值域；式（17）表示船舶滞期时间的定义；式（18）表示0,1变量约束。

5 实例验证与分析

5.1 实验相关数据

本文引用Y港连续三天内的到港10艘船舶数据作为研究数据进行分析。Y港属于连续型岸线，岸线长度为525m，岸线上有5个岸桥，将岸桥从左至右依次编号为1-5号，岸桥的初始位置见表1。有17辆内集卡可为岸桥作业服务。

表1 岸桥初始位置

Cb表示船舶在泊单位作业时间成本，取值50元/min，Cq表示岸桥的单位作业时间成本，取值为15元/min，Cc表示每辆集卡的单位作业时间成本，取值为5元/辆/min，rqc表示集卡等待岸桥的时间成本，取值为8元/min。岸桥的装卸速度为3min/TEU，有重叠靠泊区域的船舶取时间间隔为10min，同时靠泊的船舶取安全距离为10m。

根据计划期内的船舶到港顺序进行编号。具体计划期内到港船舶的信息见表2，其中船舶的预期到港、预期离港、装卸箱量、偏好位置以及单位滞期成本已知。船舶偏离偏好位置的偏移成本取每个箱子每偏移1m产生0.05元的成本，以此计算得到计划期内每艘船舶的偏移成本。

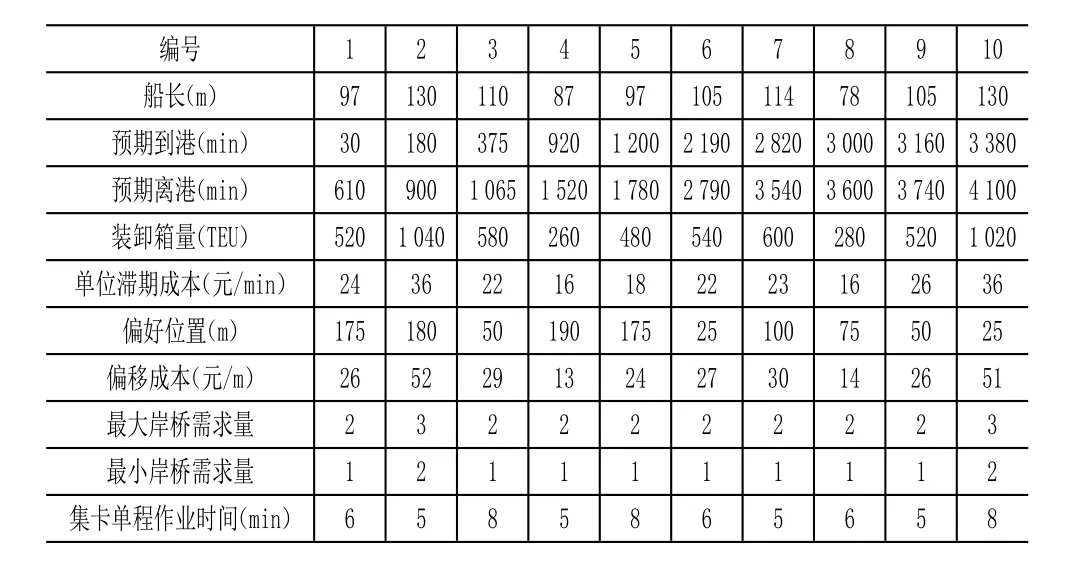
表2 船舶到港信息

5.2 优化方案结果

本文模型采用遗传算法进行求解。试验后确认适合的遗传参数为：种群大小150，最大遗传代数500，交叉率为0.8，变异率为0.07。按照上述参数，通过设计的算法进行求解，在遗传迭代330代左右出现最优解。求解时间总共花费506.778 21s。最终得到优化方案见表3。其中与时间相关项目单位为min，与距离相关项目单位为m。5-9行表示岸桥1-5任务量的分配情况，单位为TEU，10-14行表示为各岸桥配备集卡数量，单位为辆。

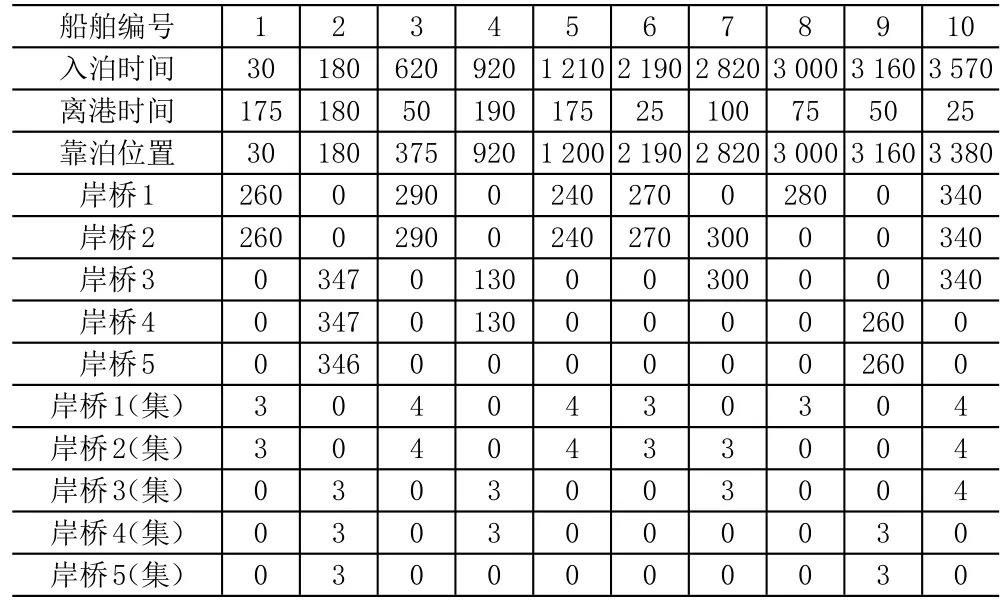
表3 优化方案结果

将优化方案具体分解得到泊位分布图与岸桥-集卡联合分配图，如图1、图2所示。

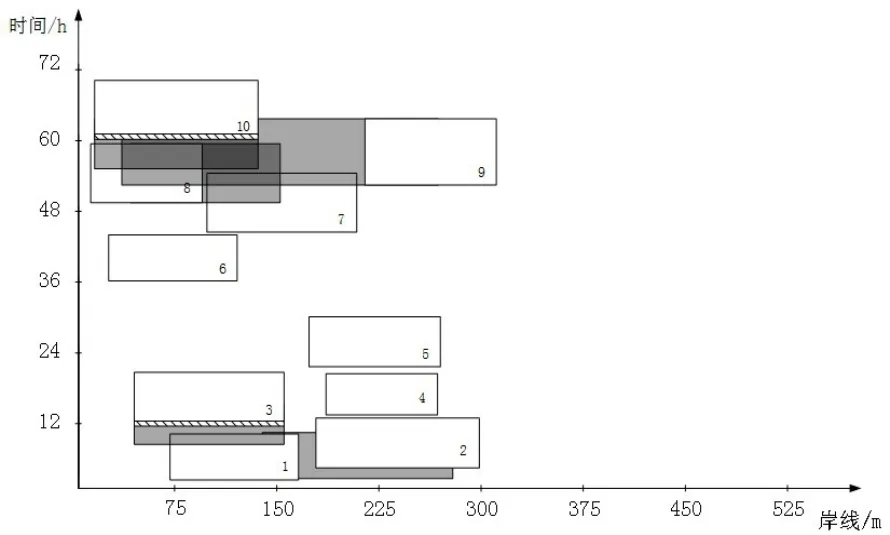
图1 优化方案泊位分布图

如图1所示，横坐标轴表示岸线长度，可显示船舶具体靠泊位置；纵坐标轴表示时间，可显示计划期内各船舶的在港作业时间占比。其中白色矩形代表到港船舶，矩形右下角编号表示船舶序号，图中矩形横向连接的阴影部分表示对应船舶发生了入泊位置与偏好位置偏移，矩形纵向连接的阴影部分表示对应船舶入泊时间与计划时间产生了向后推移，若纵向连接的阴影部分与白色矩形中间存在斜线图示，则表明对应船舶在时间推移后产生了延误船期的成本。由图1可知优化方案中产生位置偏移的有船舶1,8,9共计3艘船舶，发生入泊时间后延的有3,10两条船舶，且均产生误期成本。

如图2所示，纵坐标轴表示五个岸桥，横坐标轴表示时间。中间的矩形块表示给各个岸桥分配的集卡，矩形长度表示集卡的工作时间，且各集卡的作业开始时间与船舶的作业开始时间相同。矩形右侧编号表示集卡编号，矩形左侧ship标志集卡服务的船舶编号。当矩形后存在阴影矩形时，表示情况为集卡按效率已完成水平运输任务然而船舶仍未离港，此时的阴影表示存在集卡等待岸桥的惩罚成本。由图2可知，优化方案中存在集卡等待岸桥成本的有为船舶2工作的集卡7-15，为船舶4工作的集卡10-16，为船舶9工作的集卡10-15。本优化方案最多同时使用17辆集卡，符合该港口资源数量约束。

图2 优化方案岸桥-集卡联合分配图

5.3 实验结果分析

将优化方案的成本具体估算与初始方案数据比较得到表4，可以看到优化调度方案正常作业占比高于未优化的初始方案，成本方面整体优化11.04%，证实了优化方案的可行性。

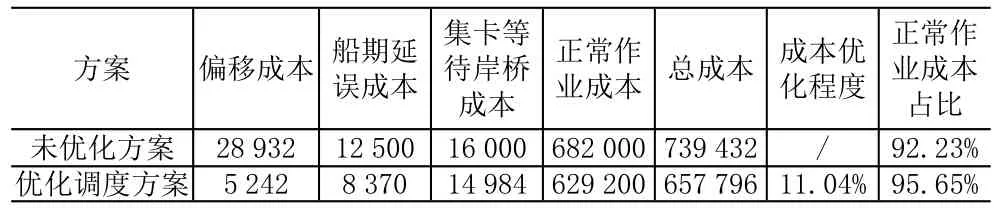
表4 优化方案与原始方案成本对比表