保持架间隙对变速球轴承动态特性影响的仿真及试验验证
屈驰飞,邓四二,姜维,谢鹏飞
(1.河南科技大学,机电工程学院,洛阳 471003;2.洛阳轴承研究所有限公司,洛阳 471039;)
1 仿真分析模型
1.1 仿真数学模型
1.1.1 钢球与保持架的作用力
钢球与保持架兜孔的法向作用力如公式(1)所示[1-2]。
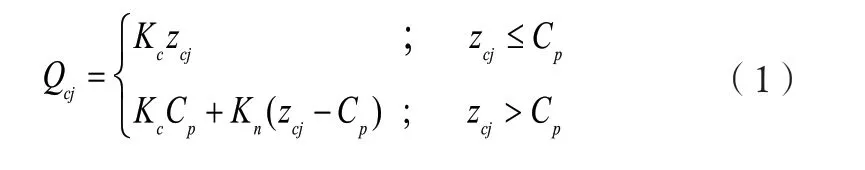
式中:
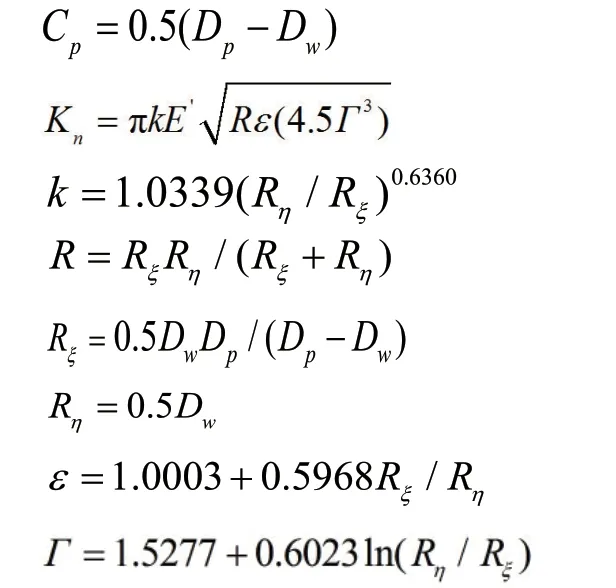
由理论分析可知,钢球和保持架间作用力与接触变形量和兜孔间隙等参数有关。
1.1.2 引导套圈和保持架的作用力
由于流体动压效应的存在,如图1 所示,将保持架定心表面与套圈引导表面看成是有限短的厚膜作用轴颈轴承的一个特例。
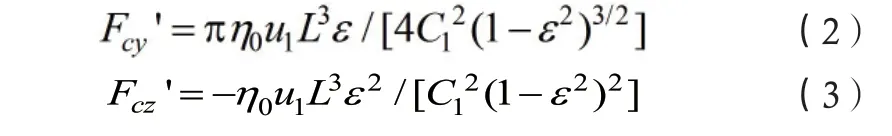
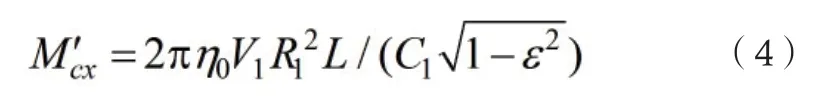
式中:
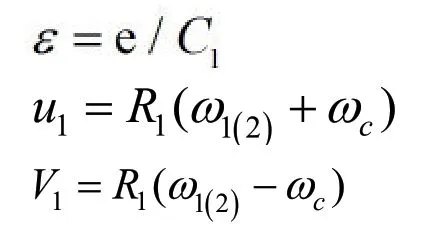
1R 为保持架定心表面半径; 0η 为润滑油的动力黏度;1C 为保持架引导间隙;L为保持架定心表面宽度;e 如图1中标注;1u 为润滑油拖动速度;ε 为保持架中心相对轴承中心偏移量;cω 为保持架角速度;1V 为两表面相对滑动速度;为轴承外(内)圈角速度。
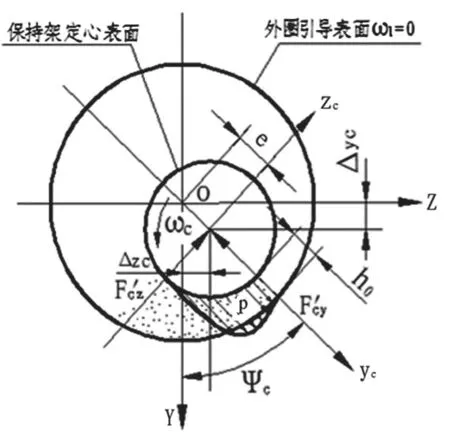
图1 保持架与引导套圈的几何接触关系
在建立保持架平衡方程时,需将保持架局部坐标系 Sc中的力及力矩投影到轴承静坐标系中,如公式(5)所示。

式中:
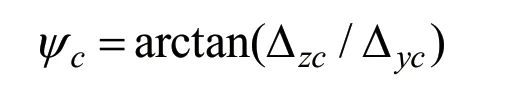
由此可知,保持架与引导挡边间的作用力与保持架外径、宽度、引导间隙、润滑油黏度和拖动速度等参数均有关。
1.2 仿真求解过程
通过ADAMS 软件系统中的CMD 语言,开发了参数化变转速球轴承保持架动态仿真分析模型[3-5],并建立轴承各个零件间的相互接触数学模型,用FORTRAN 语言编写保持架作用力子程序。通过FORTRAN 中的子程序SYSARY读取ADAMS 软件中每个步长的系统状态值,计算出该步长相应的解,再通过RESULT 传递给ADAMS 软件的求解器,完成积分求解,如图2 所示。
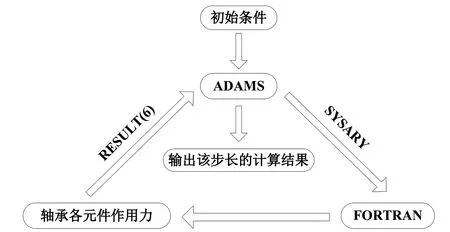
图2 动态仿真分析求解过程
2 仿真分析结果
电机所使用的某型号轴承主要结构参数见表1,利用轴承仿真模型对变速运转轴承保持架在不同间隙下的动态特性进行仿真分析。轴承转速曲线如图 3 所示,保持架间隙方案见表2。
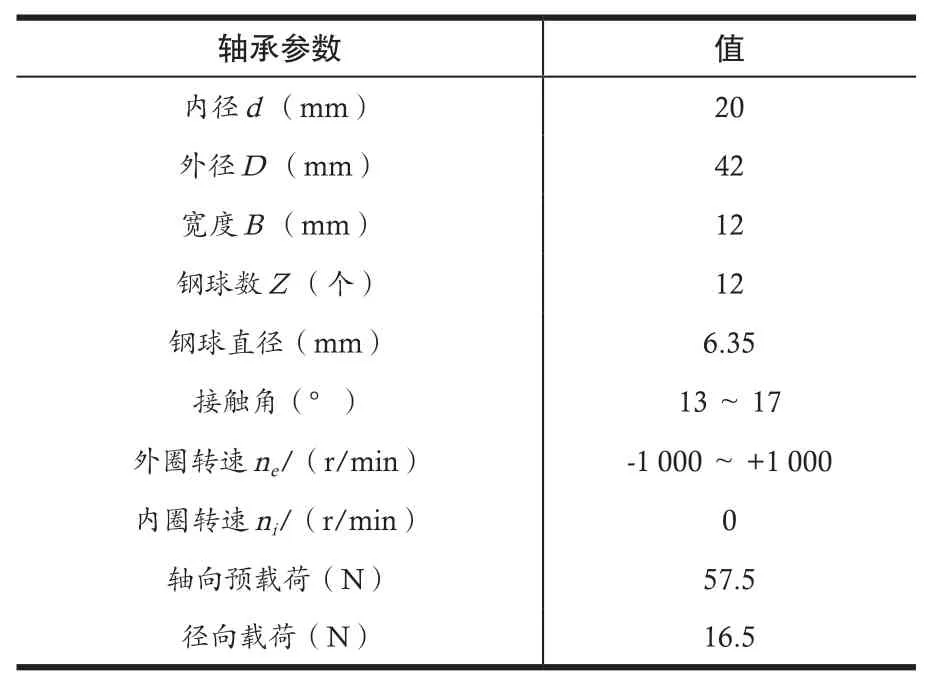
表 1 轴承参数表
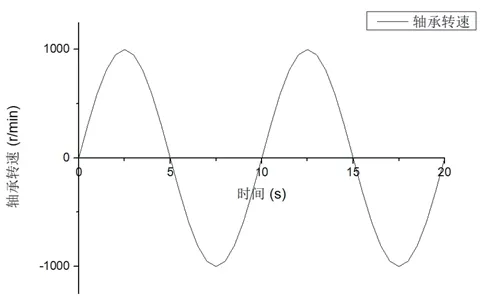
图 3 变速运转轴承转速曲线

表2 保持架间隙方案(单位:mm)
分析轴承在过零瞬间5s 内的动态性能,在仿真开始时给钢球和保持架的速度设定一个初始值,在仿真计算约0.1s后,保持架和钢球的转速趋于稳定。
2.1 保持架受力分析
假定轴承轴向载荷为57.5 N,径向载荷为16.5 N,变速运转轴承转速曲线如图4 所示,将转速变化区间设置为+1 000 r/min →0 r/min →-1 000 r/min,图5 为轴承转速过零瞬间,不同保持架兜孔间隙和保持架引导间隙组合中,保持架与引导套圈间的最大作用力曲线。
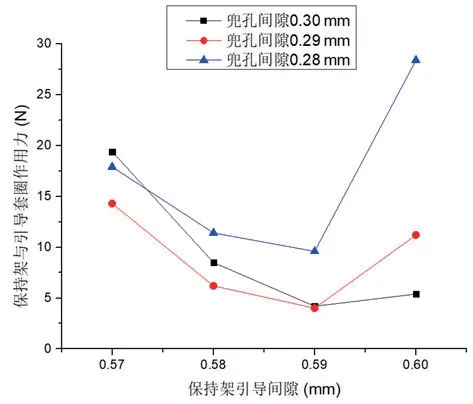
图4 不同间隙下的保持架受力变化曲线
由图4 可以看出,在变速运转轴承的应用过程中,当保持架兜孔间隙一定时,随着保持架引导间隙的增加,保持架与引导套圈间作用力先减小后增加。在这个工况中,存在一个最佳的引导间隙,可以使保持架和引导套圈之间的作用力最小。保持架与引导套圈间作用力较小的四种方案编号分别是:6、7、9 和10,其中方案10 的保持架与引导面间的作用力最小。
2.2 保持架打滑率对比分析
轴承保持架打滑率如公式(6)所示。

式中:

ncl为保持架理论转速;n 为保持架实际转速。
保持架打滑率反映了保持架实际转速与理论转速的差值。保持架打滑率越低,钢球与沟道之间的滑动成分越少,滚动成分越多,保持架实际转速与理论转速越接近,则越有利于保持架的运转稳定,由滑动引起摩擦与磨损越小;相反,保持架打滑率越高,越不利于保持架的运转稳定性。
保持架不同兜孔间隙和不同引导间隙组合下的轴承转速过零瞬间保持架最大打滑率曲线如图5 所示。
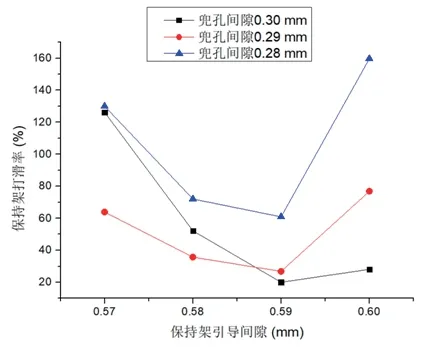
图5 保持架最大打滑率变化曲线
由图5 可以看出,在变速运转轴承的应用过程中,当保持架兜孔间隙一定时,随着保持架引导间隙的增加,保持架最大打滑率先降低后升高;当保持架兜孔间隙一定时,存在一个最佳的保持架引导间隙使得保持架最大打滑率最低;在轴承转速过零瞬间,保持架的最大打滑率均在20%以上,说明此时钢球在沟道内的滑动较大;保持架最大打滑率较低的四种方案编号分别是:6、7、9 和10,其中方案10 的保持架最大打滑率最低;保持架与引导套圈间作用力以及保持架最大打滑率随保持架外径尺寸的变化规律基本一致,说明保持架与引导面间的作用力对保持架最大打滑率有直接影响。
2.3 保持架质心轨迹分析
根据上述分析结论,对方案6、7、9 和10 的保持架质心运动轨迹进行重点对比分析,如图6 所示。
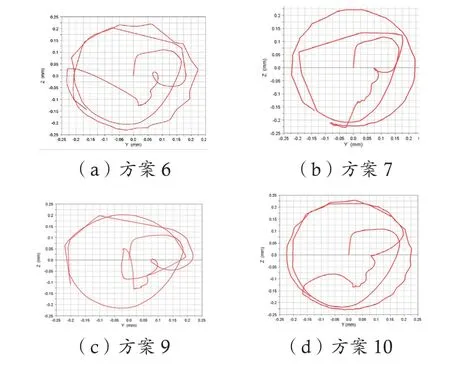
图6 保持架质心轨迹对比
由图6 可以看出,在轴承过零变速过程中,保持架出现了类似菱形的质心轨迹,质心轨迹比较紊乱且有较大的斜向位移,这说明过零变向过程中保持架受到了较大的冲击力,导致保持架质心位置突然发生改变;经过分析对比,方案6、10 的质心运动轨迹较为平滑,方案7、9 保持架质心运动轨迹相对较为混乱,保持架质心的菱形轨迹较多。
3 试验验证
根据仿真结果,制定了四组试验方案。考虑到试验的可操作性,在选配保持架间隙时将公差控制在±0.005 mm,轴承预载荷的公差控制在±1 N;具体试验参数如表3 所示。

表3 保持架及预载实测值
试验步骤如下。首先,电机在1 000 r/min 条件下运转20 小时,待电机运转电流稳定后,按图3 所示的转速曲线进行余弦运转过零试验,周期10 s,每个周期过零2 次。具体试验流程如图7 所示,电机总运转时间200 小时后试验结束,整个试验过程中电机转速过零115 200 次。
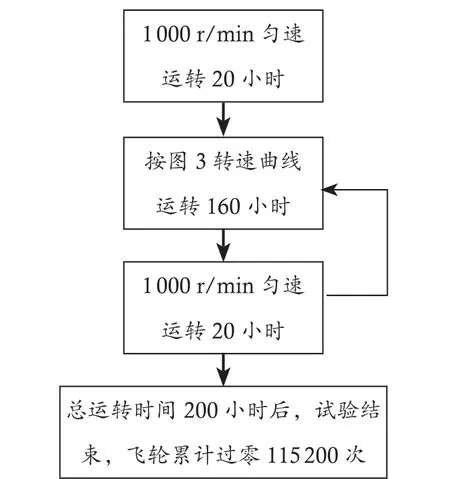
图7 试验流程
变转速试验结束后将电机分解,首先对轴承单元的轴向预载荷进行了复测。经测试,四种方案轴承的预载荷在试验后均未发生变化,说明轴承未出现异常磨损。
对轴承进行分解,对比四种试验方案保持架的接触情况,拆解后保持架如图 8 所示。对保持架引导外径、兜孔的表面接触磨损情况进行分析。接触痕迹越浅,说明磨损越轻微,轴承运转稳定性越好;相反,接触痕迹越深,说明磨损越严重,则轴承运转稳定性越差。

图8 四种试验方案保持架的接触情况
4 结语
利用仿真分析模型,对变速轴承保持架不同间隙条件下轴承保持架与引导套圈的作用力、打滑率以及质心运动轨迹进行分析,得出如下结论。
(1)在变速运转轴承应用过程中,当保持架兜孔间隙一定时,随着保持架引导间隙的增加,保持架与引导套圈间作用力和保持架最大打滑率先降低后升高。
(2)保持架兜孔间隙和引导间隙存在一个最佳的匹配关系,使得保持架与引导套圈间作用力最小;同时存在一个最佳匹配关系使得保持架最大打滑率最小。
(3)试验验证,保持架与引导套圈间作用力、打滑率越高,保持架质心轨迹越不稳定,运转后的保持架磨痕越深,电机工作越不稳定。

