模型化方法及物理图像在推导平面简谐波波函数中的作用

谭兴毅 贺叶露

[摘 要] 该文利用物理学中特有的模型化方法和物理图像定性地给出了介质质元的振动频率、振幅等于波源频率、振幅，同时也说明了波源相位与介质质元相位间的关系，在此基础上，利用时间落后法推导了平面简谐波的波函数。

[关键词] 模型化方法;物理图像;平面简谐波;波函数

[作者简介] 谭兴毅（1982—），男，博士，重庆三峡学院物理系副教授，主要从事物理教育与研究。

[中图分类号] G451.2    [文献标识码] A    [文章编号] 1674-9324（2020）23-0261-02    [收稿日期] 2020-01-06

一、引言

波动是自然界最常见的一种运动，眼见的波动如可见光、水波，而耳听的波动就是声波，这是我们认知自然界最基本的两种手段。所以，了解学习波动极其重要。大学物理中波动的学习是以平面简谐波知识作为载体，而描述平面简谐波的波动特征是平面简谐波的波函数，显然具有极其重要的地位[1-6]。实际上，平面简谐波波函數不仅描述了平面波的各种特征，如振幅、圆频率、波速和相位，还是后续知识如能量、能量密度、能流甚至波的干涉和衍射的基础，所以能否理解、掌握平面简谐波的物理意义，对后续的学习至关重要。现行的大学物理教材对平面简谐波的波函数的推导主要有时间落后法、相位落后法、动力学法[7-10 ]。然而，现行教材中的时间落后法、相位落后法大都是直接认为波的频率、振幅应该等于波源的频率、振幅，并没有相应地论述，致使学生在学习过程中很难理解;而动力学法虽然能给出二者间振幅和频率的关系，但是对数学基础要求较高，学生在学习大学物理时，并没有学习数学物理方法，所以很难给出正确的解。本文利用物理学中特有的模型化方法和物理图像定性地给出了介质质元的振动频率、振幅等于波源频率、振幅，同时也说明了波源相位与介质质元相位间的关系，然后利用时间落后法推导了平面简谐波的波函数。

二、物理图像与弹性介质模型

生活中，人们一提到“波”的概念，你可能马上就想到一颗石子掉入水中激发的粼粼微波，或者会想到绳子抖动蛇状向前的图像，又或者是马上会联想到听到的美妙音乐——声波。无论是看到的水波、绳波，还是听到的声波，其实我们都在头脑中构造了一幅图像，从物理学的角度看，这就是物理图像。

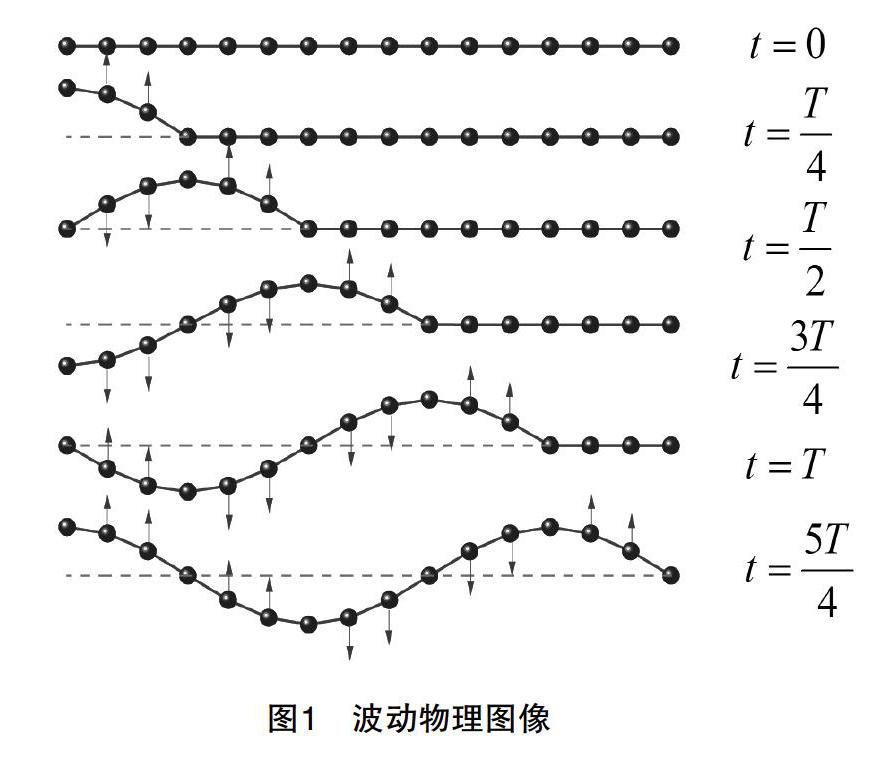
那么波的物理图像是什么样的呢？我们为了比较准确地给出波的物理图像，还得借助一个理想化模型——弹性介质。所谓理想化模型方法，其实就是哲学里面的抓住主要矛盾，忽略次要矛盾。此处，我们以弹性细绳给出弹性介质模型。首先，我们把弹性细绳看作是很多微小的质量微元（质元，图中黑色小球）组成，如图1所示（以横波为例），相邻质元之间的作用力为弹性力，即可以认为中间用不计质量的轻弹簧（图中箭头短线）连接，T为简谐振动周期。当第一个质元（可看作波源）向上运动时，第一个质元和第二个质元之间出现相对位移，中间不计质量的轻弹簧发生形变，第二个质元受到第一个质元对它的弹性力作用，在该弹性力的作用下，第二个质元也向上运动，就这样，第二个质元带动第三个质元，第三个质元带动第四个质元……就和多米诺骨牌一样，振动就从波源传播出去，形成了波。我们对该图像用物理语言稍加整理：（1）机械简谐波，即波源的简谐振动在弹性介质中的传播。显然，机械简谐波的两个条件：波源做简谐振动和弹性介质，二者缺一不可。（2）弹性介质中的每个质元只将波源的振动沿着波的传播方向进行传播，形成波动图像，所有质元只在自身平衡位置做简谐振动，并不随波发生整体位移。这样看来，波动其实是波传播方向上，介质质元的集体振动。由于每个质元都是由前一个质元带动的，也即所有质元的运动原因都在于波源的振动，而波源是一个简谐振动，所以每一个质元都在上一个质元的周期性的驱动力运动，故介质质元的集体振动时一种受迫振动。根据受迫振动运动规律，在稳态情形下，受迫振动的频率等于周期性驱动力的频率，所以波的频率和波源的频率相同;若波源和介质是同种物质，且不考虑能量损失情形下，则有介质质元的振幅等于波源简谐振动的振幅。实际上，波源和介质一般不是同一种物质，这种情况下，我们可以把和波源接触的第一个介质质元当作波源即可。（3）既然介质质元在波的传播过程中做频率相同，振幅相同的集体的受迫振动，那么它们之间的区别在于什么地方？由图1看出，不同质元开始运动的时间不同，波源最先振动，然后沿着波的传播方向，各质元依次振动。假定波在介质中传播速度为u，某一质元距离波源为x，那么该质元振动落后波源振动的时间Δt=。

三、平面简谐波波函数的推导

有前面的波的物理图像做铺垫，显然利用时间落后法推导平面简谐波的波函数比较简单。设一平面简谐波沿x轴正方向传播，如图2所示，波的传播速度为u，波源（坐标原点O点处质元）的振动方程为：

y=Acos（ωt+φ）（1）

其中y为波源偏离平衡位置的位移，A为简谐振动的振幅，ω是简谐振动的频率，t是时间变量，是波源的初相位。设P点的坐标为x，如前所述，波源处（O点）的振动状态传播到P点所需要的时间为

因波沿x轴正向传播，因此P点的振动就落后于O点，即P点在t时刻的振动状态是O点处于t-Δt=t-时刻的振动状态，于是P点的振动方程可以写成：

由于P点任意给定，即P点为x轴上的任意一点，则方程（3）就是平面简谐波的波函数。

四、结论

本文利用弹性介质理想模型和波动的物理图像，将波动看作是介质质元集体的受迫振动，故可定性地给出介质质元的振动频率、振幅等于波源频率、振幅，同时也说明波源相位与介质质元相位间的关系，在此基础上，利用时间落后法推导了平面简谐波的波函数。

参考文献

[1]马文蔚，周雨青，解希顺.物理学[M].北京：高等教育出版社，2014：16-20.

[2]吴柳.大学物理学（下册）[M].北京：北京交通大学出版社，2014：79-80.

[3]宋士贤，文喜星，吴平.工科物理教程（下册）[M].北京：国防工业出版社，2009：160-161.

[4]赵近芳，王登龙.大学物理学（上）[M].北京：北京邮电大学出版社，2017：153-154.

[5]李松林，程学勤.用波动和振动图线讲授平面简谐波方程[J].华中师范大学学报（自然科学版），1988，22（3）：387-390.

[6]張勇.关于平面简谐波波函数相位问题的研究[J].物理通报，2017，（7）：15-16.

[7]向群.论平面简谐波波动媒质体元的振动本质[J].四川教育学院学报，2012，（28）：121-123.

[8]方保龙，陈锋.平面简谐波波函数的几种导出方式及其比较[J].合肥学院学报（综合版），2018，35（5）：23-26.

[9]杨百愚，冯大毅，张崇辉，等.如何“写”出平面简谐波的波函数[J].物理与工程，2008，18（5）：9-12.

[10]杨瑞.如何求解平面简谐波的波动方程[J].科技资讯，2007，（18）：149.

On the Effect of Modeling and Physical Image in Deducing the Plane Simple Harmonic Wave Function

TAN Xing-yi，HE Ye-lu

（Department of Physics，Three Gorges University，Chongqing 404100，China）

Abstract：This article qualitatively gives the vibration frequency and amplitude of the medium mass element equal to the wave source frequency and amplitude using the unique modeling method and physical image in physics，and also explains the relationship between the wave source phase and the medium mass element phase.On this basis，the time-lag method is used to derive the wave function of the plane simple harmonic.

Key words：modeling method;physical image;plane simple harmonic;wave function