地震下斜坡桩场地及桩基动力响应的数值分析
贺 炜,陈宇林,李小星,刘剑锋
(长沙理工大学 土木工程学院,湖南 长沙 410114)
0 引言
在对已有桥梁震害资料的统计分析中,发现斜坡在地震作用下发生的变形是导致其上桥梁桩基损坏的重要原因之一[1-2]。2008年汶川地震中,新房子大桥右线的傍山线桥梁的震害,就是由于其所在的斜坡土层发生向临空侧的滑移、沉陷,导致桥墩柱产生明显的倾斜[3]。
目前,国内外学者对于地震下斜坡段桥梁桩基的震害问题研究成果较少,现有研究工作集中于边坡加固的抗滑桩和液化场地的桥梁桩基地震响应问题。离心机振动台试验与数值建模分析是两种常用的分析方法。张华等[4]通过分析连续的现场监测数据,研究了地震发生前后斜坡堆积体的变形特性和其随时间变化的规律。Yu等[5]通过对抗滑桩加固砂土边坡进行离心机振动台试验,研究了边坡的地震动力响应和抗滑桩上弯矩与动土压力分布形式。马小莉等[6]利用振动台模型试验,研究坡面形态和地震动参数对边坡加速度的影响,以此揭示坡形,高程及地震波参数等对边坡动力响应的影响。Jenny等[7]结合离心机试验数据,对比OpenSees和FLAC两款数值软件和其所用的理论方法在采用多屈服面模型和边界面模型在评估成层液化土层地震场地反应的差异。Su等[8]建立起群桩支撑码头的三维有限元动力响应模型,结果表明斜坡土体的变形机制很大程度上影响了与码头甲板刚性连接并埋入斜坡土体桩基的动力响应。尹平保等[9]借助室内模型试验,研究了不同坡度及桩长条件下斜坡段桥梁桩基竖向荷载承载特性,并得到了斜坡桥梁基桩竖向承载力折减系数与坡度及桩长的关系式。王晓伟等[10]建立起二维可液化河谷场地-简支梁桥整体有限元模型,探讨了场地液化对不同桥型、不同基础形式的梁式桥地震反应。张永亮等[11]提出非线性静力计算模型来研究群桩基础的非线性受力特征,并分析得到墩高、桩身配筋率及含箍率作为主要参数的影响规律。梁发云等[12]基于多屈服面模型分析了双向水平地震作用下的三维土柱非线性反应,验证了其模型用于非线性地震反应分析的可靠性。
本研究采用多屈服面模型和桩土动力弹簧模型,利用OpenSees软件[13]建立起地震作用下斜坡群桩二维有限元数值模型。在试验结果与数值计算的分析验证基础上,开展影响因素分析,以此研究地震下斜坡土体与桩基的动力响应规律及其影响。
1 桩土本构模型
1.1 多屈服面模型
多屈服面模型可以模拟出土体在动力作用下的弹塑性状态,并且有效地反映在地震荷载作用下复杂应力路径和变化加载条件下土体的应力响应现象。由Yang等[14]所参与构建的,集成在OpenSees软件中的基于围压多屈服面Pressure Dependent Multi-Yield(以下简称PDMY)模型,能有效模拟出无黏性土在往复荷载作用下的非线性变形效应,并且能反映应力应变循环滞回现象。
在PDMY本构模型中,假定弹性阶段是线性各向同性,而塑性阶段则因为应力路径而表现出非线性各向异性。其屈服函数公式如下:
(1)
其中,s=σ-pδ;p=p′+p′0;m=6sinφ/(3-sinφ)。
式中,s为偏应力张量;p′为有效平均应力;p′0为很小的正常数(一般取1.0 kPa),确保在p′为0时屈服面大小仍然有限;“:”为两个张量的双点积;m为屈服面的大小;φ为内摩擦角;α为偏应力子空间中屈服面中心坐标的运动偏张量。
屈服面在主应力空间中表现为圆锥面,而一系列共顶点的圆锥面则形成硬化区,最外侧圆锥面表面则被定义为破坏面。屈服面的空间形式如图1所示。
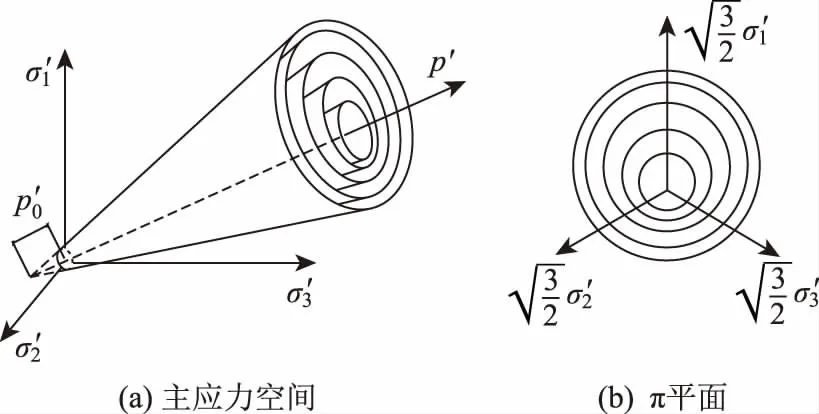
图1 多圆锥屈服面在主应力空间和π平面示意Fig.1 Schematic diagrams of multi-cone yield surface in principal stress space and π plane

图2 斜坡土-桩相互作用模型示意Fig.2 Schematic diagram of slope soil-pile interaction model
1.2 桩土动力弹簧模型
桩与土之间的相互作用采用如图2所示的一系列动力弹簧[15-17]来模拟,这些动力弹簧通过在连续的土体和桩身同位置离散化的插入非线性单轴零长度单元来表示,以此来考虑桩基础的三维动力受力效应。一共有3种类型的弹簧:p-y弹簧模拟桩周土沿桩身垂直方向上的土抗力;t-z弹簧模拟沿桩身外表面由于摩擦作用产生的竖向阻力;Q-z弹簧模拟桩端土体的承载力。
2 数值模型与验证
2.1 斜坡桩数值计算模型
通过对离心机模型试验进行相似比反算,可以建立起如图3所示的斜坡段群桩OpenSees二维有限元模型。模型的斜坡度约为27°,分为砂土和基岩两层岩土体,其中砂土层厚11.0 m,基岩面与砂层上表面平行,厚度为3.25~14.0 m。模型群桩基础桩长均为27.5 m,桩间距为2.4 m。砂土采用前文介绍的PDMY模型进行模拟,各项参数基于陈永伟等[18]根据OpenSees Manual给出的各类砂土参数的拟合公式进行取值,见表1。表中e为孔隙比,取值0.7;v为泊松比,取值0.35;Dr为相对密实度,取值50%。基岩和桩身采用弹性单元模型,其参数见表2。

图3 二维有限元模型示意(单位:m)Fig.3 Schematic diagram of 2D FE model (unit:m)

表1 PDMY本构模型参数拟合关系及取值Tab.1 Parameter fitting relationship and values of PDMY constitutive model

表2 基岩及桩基材料参数Tab.2 Material parameters of bedrock and pile foundation
模型侧边界取部分土体设置为自由场单元,其厚度远大于内部土体单元的厚度,再通过给定的位移等效命令实现周期性边界条件。底部边界设定为竖向固定,水平向采用L-K黏性边界,以模拟半无限空间弹性体下卧层吸收底部边界反射波。地震波以等效力P的形式从底部结点输入,采用文献[19]推荐的公式计算:
(2)

一般而言,要求最小网格尺寸应能保证输入地震波的最高频率的波能够顺利地通过,而最高频率的选取与地震波的特性有关,单元网格尺寸下限值应满足:
(3)
式中,四边形单元的高度Δh是根据通过岩土体的波长λmin来选择的。为了正确捕捉地震在网格中的传播,必须至少存在8个最短波长的单元,以防止相关的更高频率被过滤掉。从上文地震波处理后的频谱特性中,确定所选地震动输入中的最大频率含量(fmax)为20 Hz,取最软材料剪切波速vs为200 m/s,最终确定网格最小尺寸应不小于1.25 m。
本次离心机振动台试验(见图4)是在模型箱底部水平向输入预先设定好的地震波,地震波的形式为El-Centro波。根据振动台台面加速度计,实测得5个加载工况下地震波峰值加速度分别为 0.149 7g,0.210 6g,0.305 5g,0.430 3g,0.480 9g,各加速度时程曲线如图5所示。通过一次积分并经过基线校准即可以得到数值模型中所需对应的地震波速度时程数据,经由式(2)即可得到各数值计算工况下的输入节点等效力。

图4 离心机振动台试验Fig.4 Centrifuge shaking table test

图5 各工况实测地震波加速度时程曲线Fig.5 Time-history curves of seismic wave acceleration measured under different working conditions
地震作用下斜坡段群桩二维有限元模型的验证,通过对比5种不同加速度峰值地震波加载工况下桩身的动力响应(残余水平位移,最终弯矩)试验值与计算值,验证模型的可靠性。其中试验值通过将桩身上测得的应变值ε通过简单梁理论,满足关系式(4),可计算到测点对应的弯矩值。对得到各测点弯矩值进行7次多项式拟合[20]即可得到弯矩沿桩深度的变化关系式M(z),对其进行二次积分可求得桩身的侧向位移u,桩顶位移可通过桩顶加速度计测量加速度数据二次积分得到其位移数据,整合即可得到桩身整体位移分布。
(4)
式中,z为沿桩的深度坐标;h为应变片到桩的中性轴距离;EI为桩身的弯曲刚度。
通过图6~图7的桩身残余水平位移、桩身最终弯矩试验值与计算值对比可得:P1,P2桩残余水平位移计算值与试验值的分布基本相同,各桩坡面以下埋入段残余水平位移相差不大,但是自由段的残余水平位移有较大差别,考虑是由于桩顶加速度计受振动台振动位移和非刚性支架晃动的影响,更大的输入地震波加速度峰值导致了更大的桩顶位移误差值。P1,P2桩最终弯矩计算值与试验值呈现相同变化趋势,试验值略大于计算值,其中各加载工况下P1桩最大最终弯矩相对误差分别为7.3%,7.7%,12.5%,3.8%,9.5%,P2桩相对误差分别为4.5%,3.5%,12.4%,13.5%,11.4%,分析相对误差是由于计算时桩身采用弹性单元,与试验时模拟桩身材料的力学行为有一定的差异而导致的。
总体而言,桩身动力响应的试验值与计算值呈现相同的变化趋势与规律,虽然在数值上有一定差异,但两者相对误差对于利用数值方法探讨斜坡桩变形与受力特性分析以及开展影响因素的研究可以接受。
3 数值结果分析
3.1 斜坡桩基动力响应
图6给出了不同加速度峰值地震波加载工况下的P1和P2桩的残余水平位移。从图中可以看出,在基岩面以下的嵌固部分,各桩桩身的残余水平位移基本为零,受盖梁与系梁的约束作用,群桩自由段在这两个位置的位移基本相同,综合分析可得P1,P2桩位移基本一致。桩身位移的最大值出现在桩顶,相对于0.149 7g的加速度峰值工况,其余各加载工况下,群桩桩顶水平位移分别增大了0.39,1.16,2.79,4.34倍,表明桩顶的水平位移在各加载工况下呈现非线性增加的趋势。在砂土层内,相较于0.149 7g的地震波加载工况,其他工况下斜坡坡面处桩身残余水平位移分别增大了1.39,2.24,4.28,5.89倍,表明受到地震作用下砂土层滑动的直接影响,坡面处桩身残余位移量变化大于自由段位移的变化,在设计时应该考虑坡面滑动层对桩身残余位移的影响。

图6 不同加速度峰值地震波工况下桩身残余水平位移Fig.6 Residual horizontal displacements of piles under different acceleration peak seismic waves
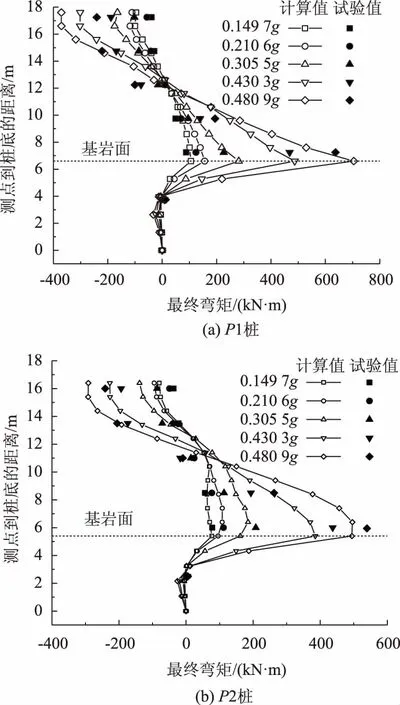
图7 不同加速度峰值地震波加载工况埋入段桩身最终弯矩Fig.7 Resultant bending moment of embedded piles in different earthquake waves
图7给出了不同加速度峰值地震波加载工况下桩身埋入段最终弯矩的分布情况。从图中可以看出,P1,P2桩身弯矩均在坡面或以下较小的范围内达到反向弯矩的最大值,其后随着测点至桩底距离的减小,在达到弯矩零点后开始出现正向弯矩,并且随后在基岩与砂土层的交界面处增大到正向弯矩最大值,最后在基岩面以下某深度减少至零,呈现非中心对称“S”形分布。同时,群桩正向弯矩的最大值较反向弯矩的大,P1桩较P2桩承受的弯矩大,说明斜坡桩在基岩与土层的交界面处是最不利截面,P1桩较P2桩在此位置承担了更多的弯矩,在设计中应作为控制截面来考虑。
3.2 斜坡场地动力响应
根据已有的离心机试验研究结果,可知地震下斜坡场地的坡肩处变形最为明显,为了更详细的分析其动力响应变化,结合数值模型中采用的PDMY模型,对斜坡场地上覆砂土层坡肩和距离坡肩7.0 m的坡顶两个位置进行斜坡场地动力响应对比分析。

图8 斜坡坡肩处各深度土体动力响应Fig.8 Dynamic responses of slope shoulder at different depths

图9 斜坡坡顶处各深度土体动力响应Fig.9 Dynamic responses of soil at slope top at different depths
从图8和图9可以看出:在深度0.5 m的地表附近的浅层土体(0~1.0 m),剪应力-剪应变滞回曲线出现明显的滑移现象,相较于坡顶处出现减弱的滞回圈现象,坡肩处基本没有形成完成的滞回圈,表明斜坡场地浅层土体尤其是坡面处土体在地震作用下基本丧失抗震能力;在深度4.5 m附近的中层土体(1.0~5.0 m),剪应变较浅层土体均出现较大的减小,坡顶处滞回曲线出现具有明显的对称性滞回圈,而坡肩处滞回曲线受斜坡的影响仍出现一定的滑移,滞回圈对称性不明显;在深度10.5 m附近的深层土体(>5.0 m),坡顶处剪应变得到进一步的减少,滞回圈更加饱满,表明此处具有良好的耗能性质,有利于结构的抗震。但该深度处坡肩位置剪应变并没有减少,反而有一定程度的增加,表明软硬岩土层倾斜交界面将加剧斜坡上覆土层动力响应,削弱其抗震耗能的能力,对软硬岩土层倾斜交界面处的桩基受力产生不利影响。
4 影响因素分析
综合考虑,本研究针对不同的斜坡坡角、上覆土层重度和桩身直径开展影响性研究。限于篇幅,本节的影响因素分析仅给出加速度峰值为0.480 9g的El-Centro地震波工况下的斜坡场地和桩基动力响应对比分析。鉴于群桩位移基本一致,同时斜坡坡肩处的动力响应较坡顶处的更具有代表性,本次影响因素分析选用P1桩的残余水平位移,群桩最终弯矩和坡肩处动力响应为代表进行分析。
4.1 斜坡坡角

图10 不同斜坡坡角时桩身动力响应Fig.10 Dynamic responses of piles at different slope angles
图10给出斜坡坡角分别为27°,30°,33°,36°和39°时,桩基的动力响应变化情况。图10(a)显示从27°增加至39°时,桩身残余水平斜坡坡角位移随之增大,其中桩顶处最大残余水平位移增幅分别为29.0%,60.7%,92.6%,122.1%,呈现线性增加的趋势。图10(b)~(c)显示P1,P2桩最终弯矩随着斜坡坡角的增大而增大,P1桩最大最终弯矩增幅为34.1%,65.0%,107.3%,143.9%,P2桩最大最终弯矩增幅为36.7%,81.0%,109.8%,129.6%,均呈现非线性增加的趋势,斜坡坡角的变化对最终弯矩的分布形式影响不大。上述结果表明斜坡坡角的增大增加了桩基的动力响应,将对于结构产生不利影响。
图11给出不同斜坡坡角下,斜坡坡肩坡面以下0.5,4.5,10.5 m处的土体动力响应变化情况。图11(a)~(c)显示随着斜坡坡角从27°增加至39°时,坡面以下各深度处剪应变均有所增加,其滞回曲线的应变滑移量增大,其中深度0.5 m处最大剪应变增幅分别为62.3%,179.5%,285.9%,366.7%,且所受剪应力也出现明显的减少;深度4.5 m处最大剪应变增幅分别为127.8%,155.6%,316.7%,361.1%,滞回圈的离散程度加剧;深度10.5 m处最大剪应变增幅分别为116.7%,133.3%,141.7%,183.3%,上述结果表明斜坡坡角的增大加剧斜坡坡肩土体的各深度动力响应,对浅层土体和中层土体的影响较深层土体的更为强烈。
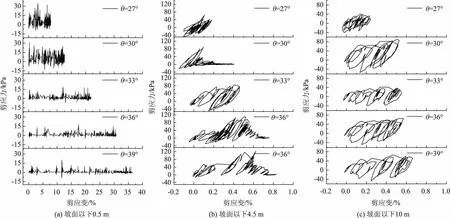
图11 不同斜坡坡角时斜坡场地动力响应Fig.11 Dynamic responses of slope ground at different slope angles
4.2 砂土重度
图12给出上覆砂土层重度分别为17,18,19,20和21 kN/m3时,桩基的动力响应变化情况。图12(a)显示随着砂土重度从17增加至21 kN/m3时,桩身残余水平位移变化不明显,其中桩顶处最大残余水平位移有小幅度的增加,最大增幅仅为5.2%。图12(b)~(c)显示P1,P2桩最终弯矩随着砂土重度的增大出现不明显的变化,其最大最终弯矩的最大增幅分别为9.8%,3.4%。本次研究中砂土重度的变化桩基的动力响应影响较小。

图12 不同砂土重度时桩身动力响应Fig.12 Dynamic responses of piles with different sand unit weights

图13 不同砂土重度时斜坡场地动力响应Fig.13 Dynamic responses of slope ground with different sand unit weights
图13给出不同砂土重度下,斜坡坡肩坡面以下0.5,4.5,10.5 m处的土体动力响应变化情况。图13显示随着砂土重度从17增加至21 kN/m3时,坡面以下各深度处剪应变均有所减少,其滞回曲线出现退化现象,其中深度0.5 m处最大剪应变减幅分别为1.5%,6.7%,11.9%,14.2%;深度4.5 m处最大剪应变减幅分别为25.3%,45.3%,46.7%,62.7%;深度10.5 m处最大剪应变减幅分别为1.7%,10.3%,12.1%,22.4%,中层土体较浅层土体和深层土体应变退化现象更为显著。上述结果表明砂土重度的增大将减弱斜坡坡肩土体各深度处的动力响应,对中层土体的影响大于浅层和深层土体。

图14 不同桩径时桩身动力响应Fig.14 Dynamic responses of piles with different diameters

图15 不同桩径时斜坡场地动力响应Fig.15 Dynamic responses of slope ground with different pile diameters
4.3 桩身直径
图14给出桩身直径分别为0.8,1.0,1.2,1.4和1.6 m时,桩基的动力响应变化情况。图14(a)显示随着桩身直径从0.8增加至1.6 m时,桩身残余水平位移随之减少,其中桩顶处最大残余水平位移减幅分别为40.2%,62.8%,70.7%,78.4%,呈现非线性减少的趋势,增大桩径有利于减少桩身残余水平位移。图14(b)~(c)显示随着桩身直径的增加,P1,P2桩最终弯矩分布形式有所变化,其中P1桩弯矩零点出现上移,P2桩坡面处弯矩减少,两桩均呈现负向弯矩出现减少而正向弯矩增大的现象。P1桩最大最终弯矩增幅为9.5%,10.3%,26.0%,31.3%,P2桩最大最终弯矩增幅为28.5%,39.6%,67.1%,83.1%,并且两者的最终弯矩值趋于相同,表明较大的桩身直径有利于调节P1,P2桩的桩身内力分配。
图15给出不同桩身直径下,斜坡坡肩坡面以下0.5,4.5,10.5 m处的土体动力响应变化情况。图15显示随着桩身直径从0.8 m增加至1.6 m时,坡面以下各深度处剪应变均有所减少,其中深度0.5 m处最大剪应变减幅分别为0.8%,1.6%,2.4%,4.0%;深度4.5 m处最大剪应变减幅分别为17.1%,31.7%,36.6%,51.2%;深度10.5 m处最大剪应变减幅分别为3.8%,21.1%,25.0%,38.5%,且滞回圈越来越饱满。上述结果表明增大桩身直径有利于减少斜坡坡肩土体的各深度动力响应,提高斜坡场地的抗震能力,但对浅层土体的影响较小。
5 结论
本研究基于离心机振动台试验结果,采用OpenSees模型进行验证及多因素分析,获得以下主要结论:
(1)数值计算与实测结果对比表明,基于OpenSees的数值模型可较好反应山区斜坡桩地震响应规律。
(2)由数值与试验结果可知,在不同加速度峰值的El-Centro地震波加载工况下,P1,P2桩身最终残余水平位移最大值出现在桩顶处,桩身弯矩最大值出现在基岩与土层交界面处。设计时宜将岩土交界面作为控制界面考虑。
(3)减小斜坡坡角或增大桩身直径均可降低地震荷载对桩基的影响,而砂土重度影响较小。3个因素对斜坡坡肩各深度处土体的动力响应均会产生影响,但其影响程度各有不同。较大的斜坡坡角会显著的增加斜坡坡肩各深度处土体的剪切变形;增大桩身直径会大幅度的减少斜坡坡肩处中层和深层土体的剪切变形,但对浅层土体影响较小。

