基于车体几何约束的全向AGV转弯路径优化*
全思博 姜一帆
学术研究
基于车体几何约束的全向AGV转弯路径优化*
全思博 姜一帆
(华南理工大学,广东 广州 510640)
可通行路径搜索及规划是AGV实现智能自主运行的关键环节。针对非圆对称移动机器人采用常规路径规划方法规划的非直线路径,特别是转弯时可能发生碰撞干涉的问题,基于车体几何约束,分析麦克纳姆轮全向AGV 3种转弯方式,给出各方式实现转弯变向的对应限制、判据及轨迹求解的方法,并讨论不同应用目的下转弯方式的选择。
全向AGV;可通行路径;路径规划;转弯变向;几何约束
0 引言
随着社会经济的发展及各国智能制造战略的推进,制造方式逐渐向客户个性化定制和柔性制造方向发展,车间生产线和仓库物品日益趋向批量小而品种繁多,这要求输送装备能根据经常变化的制造环境而智能化地柔性输送。在车间/仓库内,按非预定路径自主导航运行的自动导引小车(automatic guided vehicle, AGV),正日益成为智能制造企业物流系统的重要组成部分而受到广泛关注。这类AGV属于智能移动机器人范畴,其利用自带传感器探测周围环境并根据所得信息进行路径规划及运动控制,是移动机器人自主导航的核心问题,国内外学者对相关问题进行了大量研究[1-2]。根据驱动轮系的不同,主流AGV底盘主要分为差速、全向、阿克曼等几种不同类型,其中基于麦克纳姆轮的全向底盘因特殊的轮式结构可实现任意方向的灵活平移[3],在空间运动受限的环境下有较大应用潜力[4-5]。一些文献讨论了麦克纳姆轮全向AGV的控制与路径规划问题,如文献[6]提出一种滚动窗口法与人工鱼群算法相结合的全局动态路径规划策略,并引入危险路径惩罚函数提高路径安全性;文献[7]在局部路径规划中引入弹性皮筋算法,实现机器人运动过程中的位姿调整。然而,相关研究文献在做路径规划时很少考虑车体几何形状对路径(特别是道路分叉、拐弯时)可通行策略的影响[8];对麦克纳姆轮AGV这样的全向车而言,更缺乏考虑纵向、横向自转或转弯路径可通行策略。
本文基于占据栅格地图和车体几何约束,分析全向AGV的几种转弯方式,给出各方式实现转弯变向的对应限制、判据和轨迹求解的方法,并对不同应用目的下的转弯方式选择进行讨论。
1 麦克纳姆轮平台运动特性
麦克纳姆轮是一种复合轮,主要由主驱动轮和若干从动辊轮组成,如图1(a)所示。主驱动轮轮轴平行于车体平面投影坐标系轴,在电机驱动下带动车体实现前进或后退;从动辊轮轮轴与主驱动轮轮轴呈45°安装,每个从动辊轮均可绕自身轮轴自由旋转,因此从动辊轮为主驱动轮提供沿主轮轴向运动的自由度。

图1 麦克纳姆轮、全向AGV及其车体平面投影
基于麦克纳姆轮的全向AGV运动方式有沿车体纵向(向)及横向(向)轴线的移动,沿某个角度的斜向移动,以及围绕中心轴(向)的定点自转。在运行时,虽然全向AGV理论上可以按任意方向运动,但各种方式的允许速度和运动误差不同,本文作者在先前的研究中已证明其纵向直线运动的效率和精度最高。
2 占据栅格地图及路径规划
规划移动机器人路径时,需要利用传感器获得的环境信息建立模型,即地图。占据栅格地图法将连续的二维空间离散为特定分辨率的网格点,每个点的值代表该空间被占用的概率。若AGV使用三维激光雷达扫描得到环境三维点云时,为减少计算量,可只取AGV及负载高度作为有效范围,将高度上的环境信息映射到对应的二维栅格地图上用于障碍检测。在利用栅格地图的基础上,国内外研究者提出的多种路径规划算法,其中A*算法结合最佳优先搜索(best first search, BFS)和Dijkstra算法的优点,是具代表性并应用较广的一种启发式算法[9]。本文作者用自带激光雷达的AGV小车在实验室扫描,所得信息自动生成占据栅格地图(黑色为障碍占据区域),采用A*算法得出的路径规划(虚线)实例如图2所示。
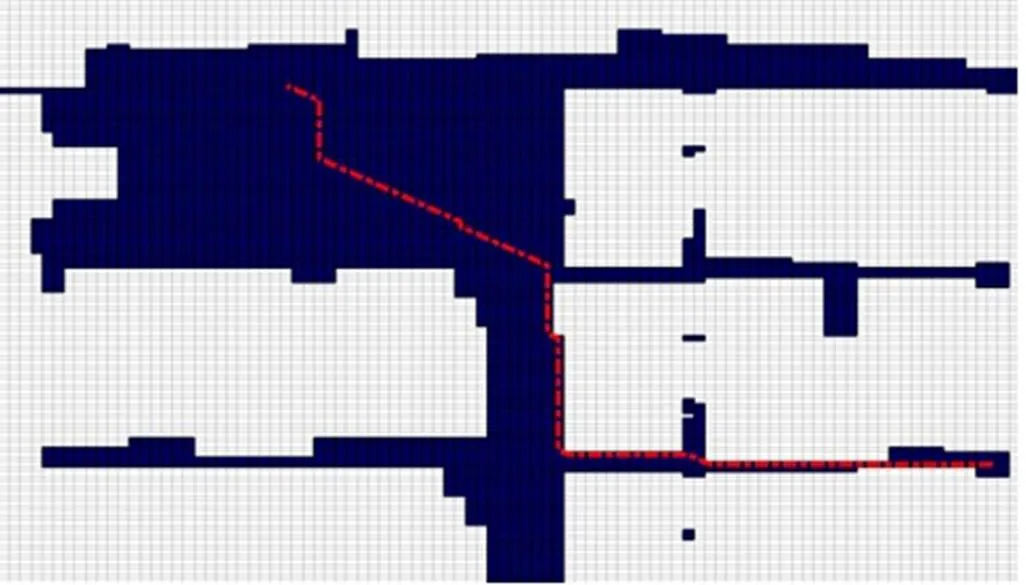
图2 占据栅格地图及路径规划实例
3 常规可通行路径规划存在的问题及解决途径
常规AGV可通行路径规划研究,几乎都是套用一般移动机器人路径搜索和规划方法,要么不考虑本体和负载形状尺寸,将之简化成一个点;要么假设本体为对称形状的球或四方体,取其半径或1/2边长作为将障碍物向道路内的膨胀量,同时将本体收缩为不占位的点,膨胀后的道路有任何空白即意味可通行。
实际上,这种忽略车体形状的方法只适用于车体为圆形的情况,即便车体为对称方形,也只能在直线路径且小车理想地控制不跑偏时才可行。一方面,现有多种算法规划的移动机器人全局运行路径普遍存在局部道路上严重偏置不居中的问题,如图2实例中虚线;另一方面,当车体转弯变向时,即便不跑偏也可能发生碰撞。
全向AGV小车转弯方式有平移、定点自转、曲径转弯等方式。全向AGV转弯变向的可通行性如图3所示:黑体填充占据栅格为障碍物;浅灰填充占据栅格为考虑小车运行安全而做出的防护虚拟屏障(不允许突破);深灰填充占据栅格为以车体半宽而作的道路收窄量;剩余为不占位空地;B点为A段与C段道路中心线交点。
如图3(a)所示:将车体收缩为一个质点,它可以从A段道路至C段道路顺利通达,转弯变向毫无问题。
如图3(b)所示:不收窄道路,考虑车体几何形状,A段路可容小车纵向行进,C段路也可容小车横向行进,但正方形车体到了转角处,若车体自转变向,就有转向所需占位大于直行占位问题,如在B点旋转就会发生干涉(但右移一格后则可旋转)。如果车体不是正方形,而是长方形或其他非对称形状,上述问题更普遍和显著。
如图3(c)所示:不收窄道路,长方形车体平移,因C段道路比较宽,车体可在B点开始沿向横行通过C段道路。
如图3(d)所示:长方形车体可沿曲径转弯(仍以正向前行),但必须适当选取起点、终点和转弯曲径。沿曲径转弯除了需要选择转向位置,还涉及车体随位置变化的姿态转变。
图3(b)、图3(c)和图3(d)在以1/2车体宽度膨胀障碍物边界,同时将车体收缩为不占位质点的规划中都反映不出来,故用常规的路径规划方法做AGV可通行路径规划无法保证小车可真正通行,更无法表达小车以何种转弯方式可通行。

4 基于车体几何约束的转弯变向轨迹确定
4.1 3种转弯方式的轨迹确定
不对称形状车体的3种转弯方式(定点自转、平移、曲径转弯),需根据车体几何形状,分别在地图上寻找适宜的横摆起始点、自转点、曲径轨迹的起点、终点和转弯半径。
不对称形状车体定点自转时,运行轨迹如图3(b)所示,需要确定车体中心在地图栅格的位置,约束条件为车体自转过程中不超出道路安全边界,且自转后车体在C段道路居中(不擦边运行安全性更高,且可快速运行)。显然,需满足的条件有:1)自转点与道路安全边缘的距离不小于1/2车体对角线长;2)自转点位于C段中心线上。小车自A段前行,从车体尾边超过C段道路安全下缘开始,向右前方行进,需判断车体中心点是否与任何安全屏障距离不小于1/2车体对角线长,同时判断车体中心是否达到C段中心线。AGV以定点自转方式转弯变向如图4所示,车体中心轨迹为虚线,车体沿线平移,车体中心到达D点即满足变向要求,且符合行进路径最短原则,在此自转所需角度,转后车体纵轴与C段路中心线重合,正向直行。自转流程图如图5所示。
不对称形状车体由沿纵向变为沿横/斜向行进,运行轨迹如图3(c)所示,其变向点的确定简单直观。小车沿A段道路纵行,当车体中心达到C段道路中心线的B点时,判断C段道路宽度是否大于车体长度,若是,则变为以C段路中心线横/斜移。对应流程图如图6所示。
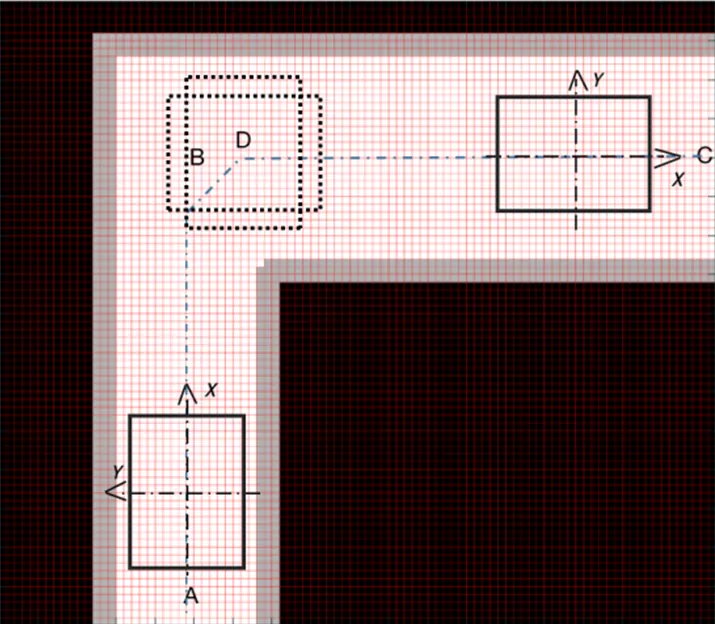
图4 AGV以定点自转方式转弯变向

图5 定点自转流程图
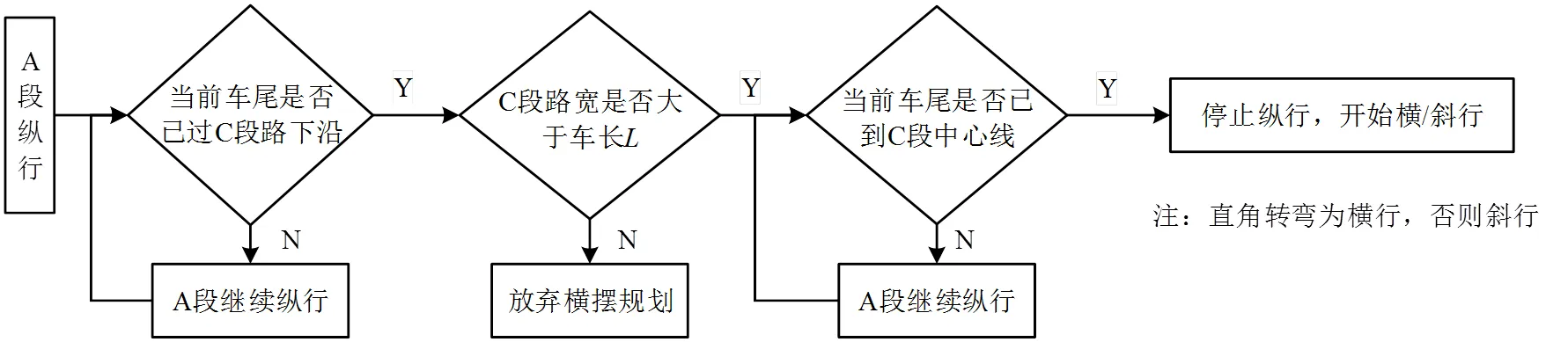
图6 横/斜摆转弯流程图
车体沿曲径转弯时,需选取曲径轨迹的起点、终点和转弯曲径。转弯曲径未必是定半径和圆心的一段圆弧,不同的A段和C段道路宽度,起点、终点和转弯曲径可能不同。AGV以直角转弯方式变向如图7所示,可沿定心圆弧,以A段和C段道路中心线为两切线、一定半径作圆,得到圆弧起点和终点,转弯后车体保持在C段道路居中。理论上,最小半径应大于车体半宽,且弧线曲率越大转弯越困难,需控制角速度越小。
当AGV以非直角转弯方式变向时,非定半径和圆心的曲径轨迹解决方案为:首先,忽略车体尺寸,对A*算法得到的车心预定路径进行顺滑处理(如贝塞尔曲线拟合[3]),转弯起始和结束后分别与A、C段道路中心线相切,尽量不产生加速度突变;然后,以路径上栅格地图前后两步车心连线为车体纵向中心线,确定各点位之间车体变向角度,并用车体尺寸进行干涉校验,如有干涉则剔除该点后重新规划路径;最后,当转向角度为零,即转弯结束时,小车在C段路上以正向直行。沿曲径转弯流程图如图8所示。
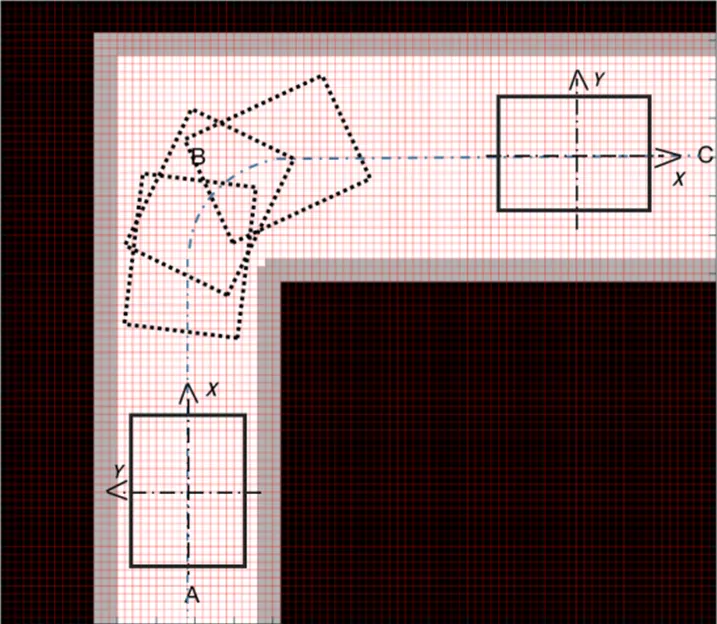
图7 AGV以直角转弯方式变向
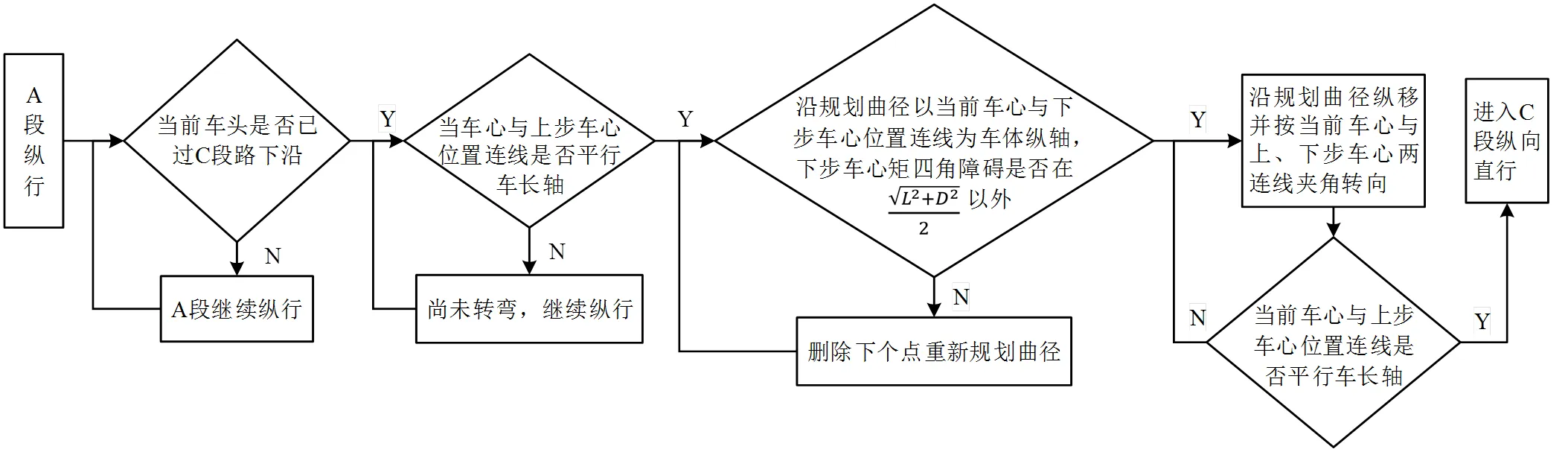
图8 沿曲径转弯流程图
4.2 转弯方式的选择
在道路转弯处,依据上文判断车体转弯方式和转弯路径。如果3种转弯方式皆可行,则根据实际应用目的以某种标准优选一种方式。
从转弯方式及转弯所需占用面积方面考虑,以直角转弯为例,车体横摆变向或斜向平移所需面积最小(车体自身投影面积);车体定点自转次之(近乎以车体对角线为直径的圆);以车体半长为最小半径的定心圆弧转弯和以最短路径规划出的非定心曲径转弯所需面积最大。
从转弯方式、需要时间及路径长度方面考虑,设小车以相同速度运行(忽略小车变向停顿),车体从纵向直行到斜向平移或直接横摆运行的路长和时间最短;车体定点自转的路长和时间次之;车体沿定心圆弧线或非定心曲径转弯的路长和时间最长。
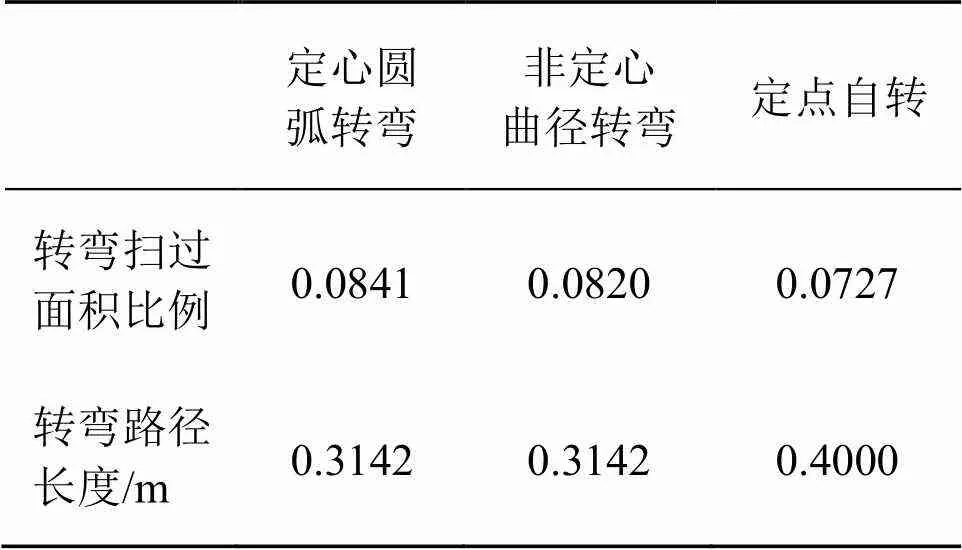
表1 转弯方式对应扫过面积与路径长度

从小车转向加/减速引起的负载运行平稳性方面考虑,小车沿轴纵向可以较高速度行驶并获得较高运行精度;沿非定心曲径转弯使小车运行具有较好连续性;沿定心圆弧转弯方式的连续性次之(在起点和终点加速度变化而有所冲击);从纵向前行直接变到横向运行或车体定点自转,需要停车再启动换向,加/减速度引起的较大惯性力影响小车负载安全性,为克服此问题需要降低启/停加速度,从而影响运行效率。
5 结论
针对忽略移动机器人几何形状,膨胀地图障碍物情况下,机器人运行路径规划存在的非圆对称车体可能无法通行问题,根据全向AGV运动特点,指出可以平移、定点自转和曲径转弯3种方式实现转弯变向,给出3种方式对应轨迹的求解方法。车体由纵向变为横向行进扫过面积最小、路径长度最短,但需变向后道路宽度大于车长,且小车需先停顿再启动横行,加/减速度引起的惯性力影响小车负载安全性,而横向运行速度较慢、精度不高;车体定点自转变向,限制条件为该点周围需有大于车体对角线半长的圆周空间,小车自转前可能需要斜向平移才能找到适当的自转点,使自转后车体在道路上居中,且也需先停车再启动自转;小车沿非定心曲径转弯运行有更好连续性,利于保持负载安全。
[1] 王春颖,刘平,秦洪政.移动机器人的智能路径规划算法综述[J].传感器与微系统,2018,37(8):5-8.
[2] Costa M M, Silva M F. A survey on path planning algorithms for mobile robots[C]. 2019 IEEE International Conference on Autonomous Robot Systems and Competitions (ICARSC). IEEE, 2019: 1-7.
[3] 王兴松.Mecanum轮全方位移动机器人原理与应用[M].南京:东南大学出版社,2018.
[4] 梅柯,锁少伟,王静,等.麦克纳姆轮AGV在汽车焊装车身转运中的应用[J].自动化应用,2018(5):10-13.
[5] 方玉发.基于麦克纳姆轮的重载AGV关键技术研究与应用[D].杭州:浙江大学,2019.
[6] 李文涛.全向AGV运动控制及路径规划研究[D].西安:西安科技大学,2019.
[7] 靳士超.基于麦克纳姆轮的全向智能移动机器人导航系统研究[D].苏州:苏州大学,2018.
[8] Kennedy M, Thakur D, Hsieh M Ani, et al. Optimal paths for polygonal robots in SE (2)[J]. Journal of Mechanisms and Robotics, 2018, 10(2):021005.
[9] Guruji A K, Agarwal H, Parsediya D K. Time-efficient A* algorithm for robot path planning[J]. Procedia Technology, 2016, 23: 144-149.
Optimization of Turning Path of Omni-Directional AGV Based on Geometric Constraints of Vehicle Body
Quan Sibo Jiang Yifan
(South China University of Technology, Guangzhou 510640, China)
Search and planning of passable path is the key to realize intelligent autonomous operation of AGV. The common research method of path planning for mobile robots is to simplify the robot body into particles on 2-D map and simply inflate the contour of the obstacle, and take the reduction of road size as the equivalent of the size of the moving body. All remaining blank areas on inflated roads will be considered as passable. The analysis shows that this method is only suitable for the case that the moving body is circular, but moving body which is not circular symmetrical is likely to collide in the non-straight path planned by this method, especially in the turning section, which is actually impassable. Based on the geometric constraints of the vehicle body, this paper analyzes three kinds of turning modes of omni-directional AGV, gives the corresponding restrictions and criteria to realize the turning, and the parameters to be solved respectively; in addition, this paper discusses the choice of turning modes for different application purposes.
omni-directional AGV; passable path; path planning; turning; geometric constraints
全思博,男,1983年生,博士,主要研究方向:智能机器人应用技术、机器视觉应用技术。E-mail: quansibo@scut.edu.cn
姜一帆,男,1997年生,学士,主要研究方向:机电控制与模拟仿真。
广东省自然科学基金项目(2020A1515011503);2019年广东省普通高校特色创新类项目(2019KTSCX003)。
TP277
A
1674-2605(2020)03-0002-06
10.3969/j.issn.1674-2605.2020.03.002
- 自动化与信息工程的其它文章
- 一种离心风机蜗壳自动焊接工作站研制
- 基于力与位移同步跟踪的A型邵氏硬度计校准装置

