基于EMD-GAELM-ARIMA算法的大坝变形预测

徐肖遥，张鹏飞，蒋 剑

(1.贵州大学矿业学院，贵州 贵阳 550025； 2.中国电建贵阳勘测设计研究院工程科研院，贵州 贵阳 550081)

0 引 言

大坝结构复杂，工作状态受水位、温度等多种因素影响，而相较于渗流、应力应变等效应量，变形监测数据更能直观地反映大坝的运行状态。因此，构建大坝的变形预测模型对维护大坝的安全稳定运行有重要意义。早在20世纪，国外学者已经基于多种统计学模型，结合水压、降雨量、温度等因素，进行大坝变形预测模型的研究[1]。但由于大坝的变形是一个复杂的非线性问题，传统的多元线性统计学预测模型泛化能力较差，因此，近年来国内外学者应用在非线性问题上表现更好的人工神经网络模型构建大坝的变形预测模型[2-3]。相较于单一算法存在训练时间长、稳定性不足等缺点，GA-BP、PSO-ELM[4]等融合模型在大坝变形预测中更具可行性。因此，本文引入Huang等人[5]提出的经验模态分解，使非平稳的变形实测值平稳化，得到具有物理意义的本征模函数和残差；同时引入由Huang等[6]学者提出且已在非线性建模中得到广泛应用的具有学习效率高、泛化能力强的极限学习机进行预测模型的构建，并用遗传算法对极限学习机的输入权重和隐含层阈值进行全局寻优，从而减弱随机性误差，提高模型的泛化能力。将预测结果重构后，实测值仍存在一定误差，且难以在预测方法上进行改进，针对这一情况，本文引入差分整合移动平均自回归模型(ARIME)算法作为误差修正模型[7]，从而构建基于EMD-GAELM-ARIMA的大坝变形预测模型，大大提高了变形预测精度，强化了模型的泛化能力。

1 大坝变形预测模型

1.1 经验模态分解

由于大坝变形是一个复杂的非线性系统，受多种因素的共同影响，其变形监测序列中存在随机变化的干扰信号，长期变化的趋势分量和因降雨、水位、温度等因素影响的周期变化项。若只通过复杂的参数建立单一形变预测模型，则很难准确掌握变形的规律，导致预测的精度和效率难以满足要求。而经验模态分解是由Huang等人[5]提出的一种针对非线性、非平稳信号的自适应信号分解算法。EMD不仅从根本上摆脱了傅里叶变换的约束，具有良好的时频分辨率和自适应性，而且在不需要考虑预选小波基函数的同时还继承了小波变换的优点，能够完美地重构原始信号。EMD在分解含噪信号后，将噪声和有效信号分离在不同的本征模函数中，通过合理利用本征模函数重构信号，可以达到去除噪声的目的[8-11]。

对于一个给定的信号x(t)分解步骤如下：首先找到x(t)的所有极值点，利用三次样条差值函数对极大值点形成上包络线，对极小值点形成下包络线。计算上、下包络线的均值，记为m1(t)，则给定信号x(t)的第一个理论上的本征模函数(IMF)：

h1(t)=x(t)-m1(t)

(1)

在实际情况中，由于难以求出理论上的上、下包络线，而只能利用三次样条差值函数近似拟合。而信号中的拐点在计算的过程中可能会转换为新的极值点，而新的极值点不在第一次筛选的过程中，因此需要通过循环筛选，直至达到某种停止准则才完成迭代。即把h1(t)当作新的x(t)，循环上述操作n次得到hn(t)。即：

hn(t)=hn-1(t)-mn(t)

(2)

此时，令第一个本征模函数d1(t)=hn(t)，并将d1(t)从原始信号x(t)中分离出来，得到残差r1(t)：

r1(t)=x(t)-d1(t)

(3)

最后，将r1(t)视为新的给定信号，重复上述步骤，即可得到后续IMF分量，直至rn(t)单调或小于预定误差时，EMD分解结束。即：

(4)

其中循环筛选的停止准则为2次相邻筛选结果的标准差SD在0.2～0.3之间，本文取0.2作为停止标准。其中：

(5)

1.2 GA优化ELM模型

1.2.1 极限学习机

ELM是由输入层、隐含层和输出层组成的经典单隐含层前馈神经网络模型，其输入层与隐含层、隐含层与输出层的神经元间为全连接[12-13]。针对堆石坝变形，假设有N个样本(xi，yi)，其中xi=[xi1，xi2，…，xin]T∈Rn，yi=[yi1，yi2，…，yim]T∈Rm。对于一个隐含层节点个数为L和激励函数为g(x)的极限学习机的公式表现为：

(6)

式中，βi为输出权重，g(x)为激励函数，wi=[wi1，wi2，…，win]为输入权重，bi为第i层隐含节点的阈值。

(7)

可用矩阵表示为Hβ=T。其中H是隐含层节点的输出，β为输出权重，T为期望输出。在极限学习机中隐含层输出权值和阈值可随机给定，因此在确定激励函数后，隐含层节点的输出矩阵H为一确定的常数矩阵。因此式(7)转换为求解一个线性函数，通过最小二乘法求得该函数的最小范数为：

β=H+T

(8)

其中，H+为矩阵H的Moore-Penrose广义逆。

1.2.2 GAELM模型

遗传算法是一种高度并行的优化算法，训练个体通过复制、交叉、变异不断进化，最终收敛到最优群体，从而求得问题最优解。由于极限学习机算法的输入层与隐含层间的连接权值和隐含层神经元阈值是随机给定的，因此存在某些情况下，部分隐含层节点失效，导致ELM神经网络的预测精度降低，或者隐含层节点过多导致模型产生过拟合现象[14-16]。针对这一问题，将遗传算法和极限学习机相结合，利用GA算法对ELM神经网络的输入权值和隐含层阈值进行优化，寻求最优解，从而构建最优的ELM模型。具体参数寻优步骤如下[17-18]：

1)确认ELM神经网络的拓扑结构，将模型的输入权重和隐含层节点阈值进行二进制编码，作为初始种群，个体的维度由输入权重和隐含层阈值决定。

2)将解码得到的输入权重和隐含层阈值代入到ELM神经网络，使用训练数据训练模型，并用测试数据进行测试，验证模型精度，使预测值和实际值的残差尽可能小。

3)确认适应度函数和进化代数，求解后，对适应度较优个体进行交叉、变异、重组，产生新种群，再次计算新种群的适应度值。当达到循环最大次数，或者残差低于预设阈值时，GAELM算法结束。

1.3 ARIMA模型

原始变形监测序列经EMD分解和GAELM模型预测后得到各组IMF及残差的预测值。将预测值同实际值进行对比，得到误差序列。将各组误差序列作为ARIMA模型的原始序列，进行误差修正，从而提高模型的预测精度。模型表示如下：

(9)

其中，φm(m=1,2，…，p)为自回归模型系数；p为自回归阶数；ωn(n=1,2，…，q)为均滑动模型系数；q为滑动平均部分的阶数；at为白噪声序列。

利用ARIMA模型进行误差序列修正时，首先确认p、q的值，其次利用最小二乘法确认模型其他参数，然后拟合原始序列得到修正后残差序列z(x)，如果z(x)是白噪声的一个子序列，则修正结束；反之，继续优化参数，直到满足条件为止[19-20]。

1.4 EMD-GAELM-ARIMA模型的算法流程

首先利用EMD算法对原始变形监测序列进行处理，使非平稳的变形实测值平稳化，得到具有物理意义的本征模函数和残差。然后分别利用GAELM模型对每组数据进行训练，在融合算法中，将ELM的输入权值和隐含层阈值作为遗传优化算法中的参数进行全局寻优，减弱随机性误差，提高模型的泛化能力，从而得到各组IMF分量的预测值及趋势分量的预测值。对各组IMF分量的预测值及趋势分量的预测值进行等权相加，得到预测样本的重构预测结果。最后引入差分整合移动平均自回归模型(ARIME)算法作为误差修正模型，对重构结果进行误差修正，从而得到融合模型的最终预测结果。

2 实例验证

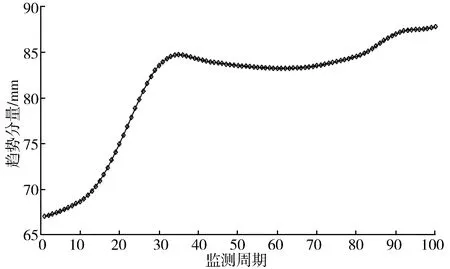
本文以某一钢筋混凝土面板堆石坝变形监测数据为例，验证EMD-GAELM-ARIMA预测模型。大坝位于贵州省乌江，最大坝高179.50 m，坝顶长427.79 m、宽10.95 m。取2005年8月3日—2007年9月5日共110组实际监测数据为样本，如图1所示。将这110组数据分为2个大组，前100组为模型的训练样本，后10组为模型的预测样本。模型的输入节点分别为时效因子、温度因子和水位因子，输出节点为大坝的变形量实测值[21-22]。

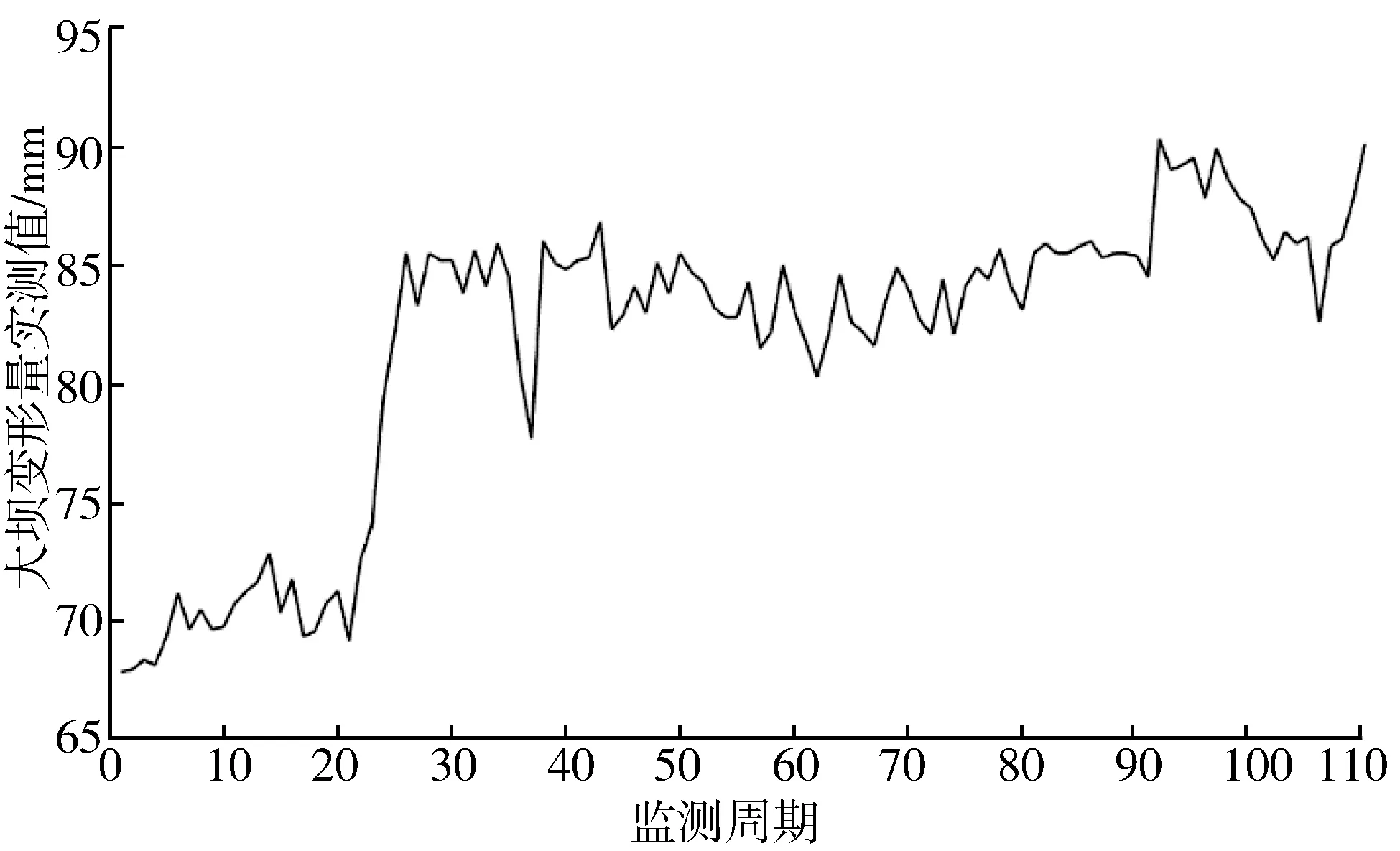
图1 大坝变形监测曲线

由图1可知，变形监测曲线中存在数处异常突变，因此为“去除”监测数据中的噪声，对原始数据进行平稳化处理，采用经验模态分解对变形实际监测数据进行分解、重构[23-24]，得到3组IMF分量和1组趋势分量，如图2所示。

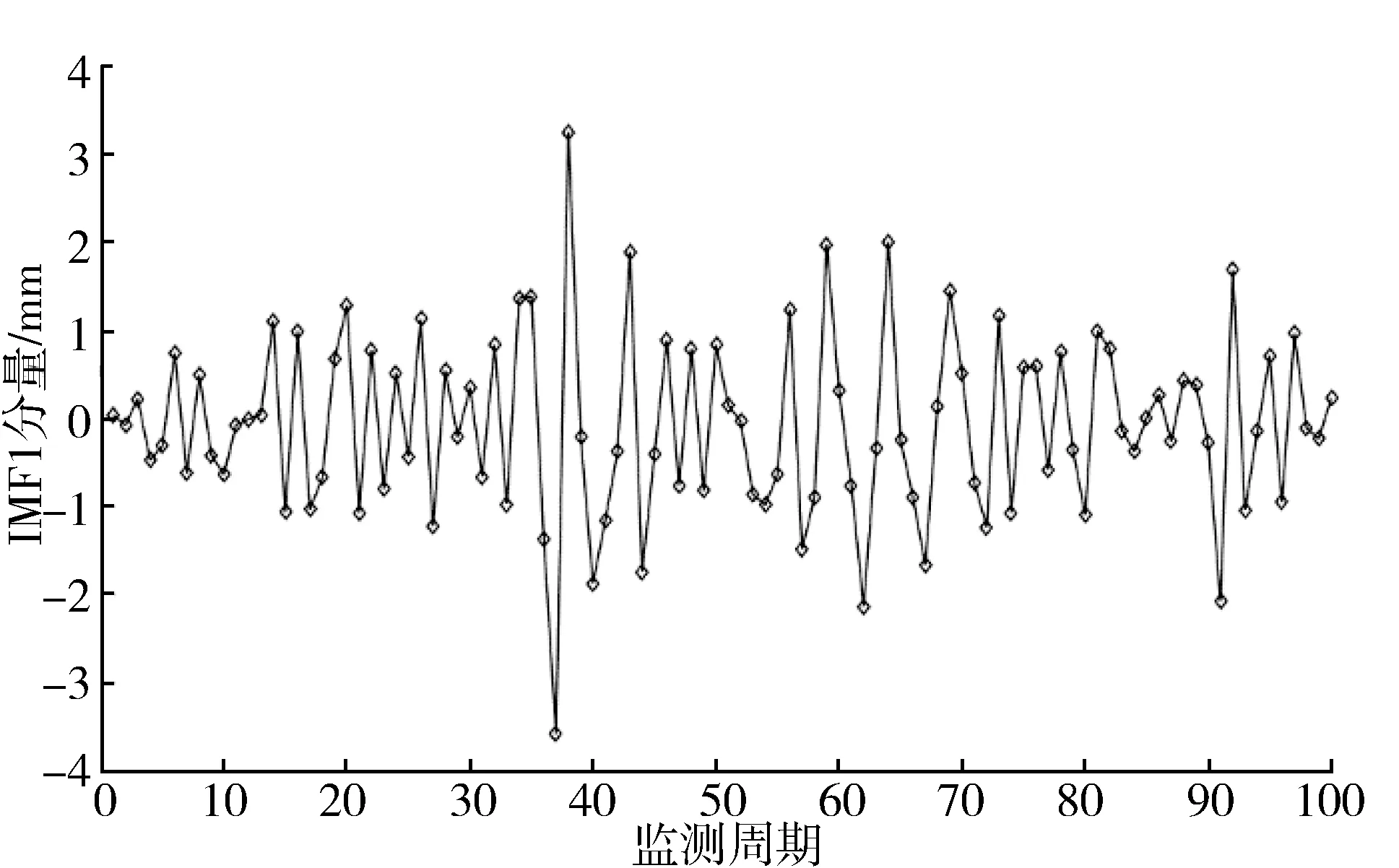
(a) IMF1分量

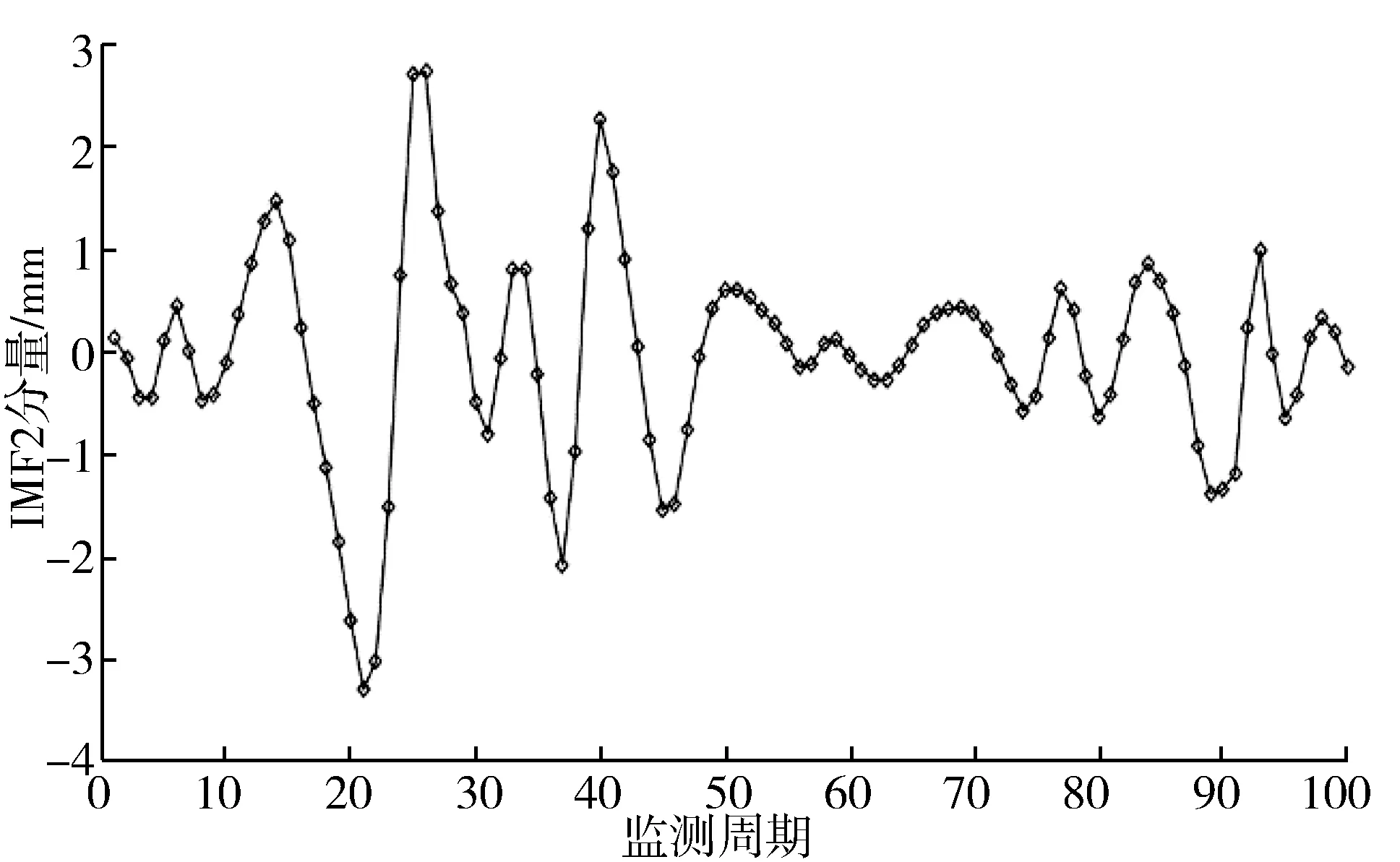
(b) IMF2分量

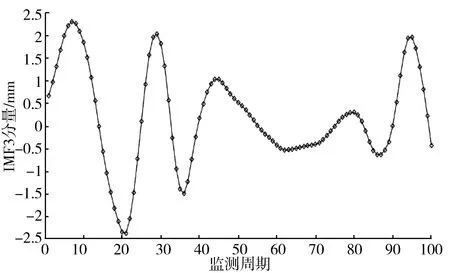
(c) IMF3分量

(d) 趋势分量R

从分解结果可以看出，IMF1频率高，振幅大，周期性不明显，平稳性弱，可认为是原始数据中的干扰信号，IMF2和IMF3周期性较为明显，可认为是受温度和水位这2个因素影响。R是趋势分量，表示大坝的整体变形趋势是上升的。分别将分解后的3组IMF和趋势分量作为算法的输出节点，将时效分量、水位分量、温度分量作为算法的输入节点，利用EMD-ELM算法和EMD-GAELM优化算法进行训练和预测。模型算法各参数取值范围如表1所示。

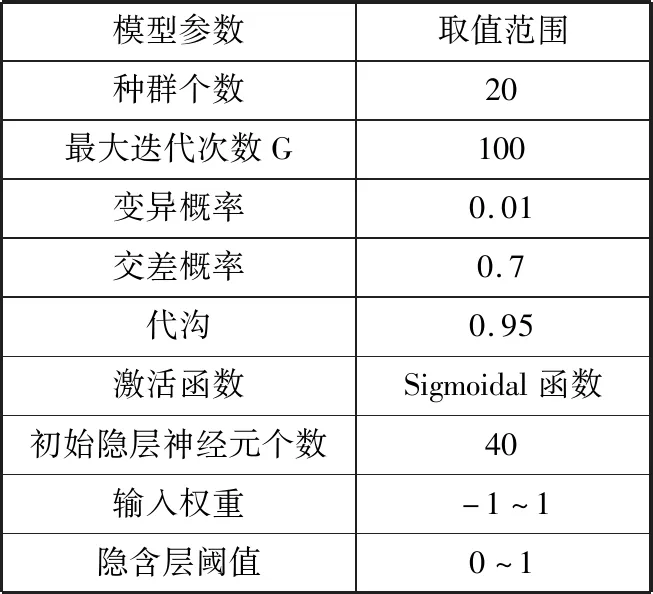
表1 模型各参数取值范围

利用EMD分解和GAELM模型预测得到各组IMF分量的预测值及趋势分量的预测值，通过将模型预测值同实际测量值进行对比，得到误差序列。在此之上，对各组误差序列进行ARIMA模型误差修正，进一步完善模型预测结果，最后对修正后的各组IMF分量的预测值及趋势分量的预测值进行等权相加，得到预测样本的最终预测结果。同时计算出单一ELM算法和GAELM、PSO-ELM融合算法的预测结果。4种模型的预测结果对比如表2所示，预测效果对比如图3所示。

表2 4种算法的预测结果对比

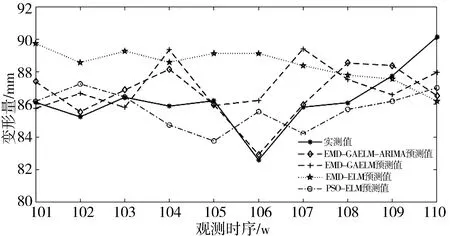
图3 4种算法的预测效果对比

由图3和表2可知，本文提出的EMD-GAELM-ARIMA组合算法的预测值残差总体更小，相较于单一ELM算法和GAELM、PSO-ELM融合算法，预测的变化趋势更接近实际监测结果。针对表2分别计算各个算法的均方根误差和平均绝对误差，进行算法的精度评定，结果汇总如表3所示。

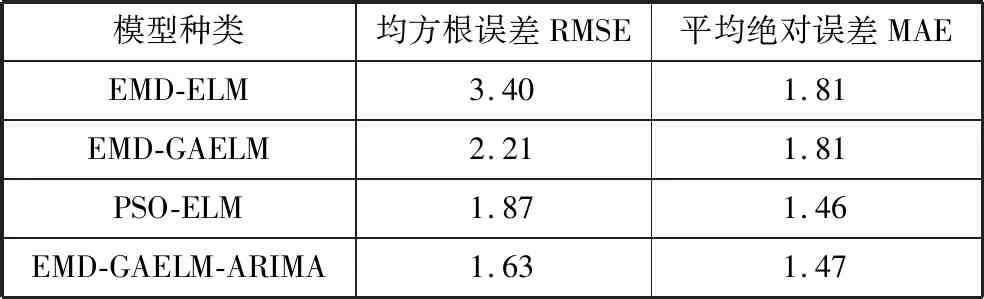
表3 各算法预测精度对比

由表3可知，EMD-GAELM-ARIMA算法的均方根误差和平均绝对误差都明显小于EMD-ELM算法和EMD-GAELM融合算法的均方根误差和平均绝对误差，较近年所提的PSO-ELM融合模型也有一定的精度提升，由此可以看出，EMD-GAELM-ARIMA算法的预测精度明显高于EMD-ELM算法和EMD-GAELM算法，结果更加稳定。相较于PSO-ELM融合模型，EMD-GAELM-ARIMA算法的预测趋势与大坝实际变形监测数据的变化趋势更为接近，模型构建更加科学合理。

3 结束语

由于大坝变形是一个复杂的非线性过程，所以大坝变形监测数据具有非平稳、非线性的性质，因此引入经验模态分解方法，通过分解重构，使其平稳化，有效提高了模型算法的预测精度；并以极限学习机为基础，采用遗传算法对ELM的输入权重和隐含层阈值进行优化，构建大坝变形预测模型，最后针对预测值与实测值的残差，利用ARIMA模型进行误差修正进而得到最终模型预测结果。通过实例验证，相较于EMD-ELM算法和EMD-GAELM算法，EMD-GAELM-ARIMA算法的均方根误差和平均绝对误差明显较小，同PSO-ELM融合模型相比，也有一定的精度提升。因此，本文提出的EMD-GAELM-ARIMA算法能够准确地进行大坝变形预测，具有更高的预测精度和适用性，验证了该模型算法在复杂的大坝变形预测中的可行性。