基于双方程的大涡模拟分析连铸结晶器内钢液流动特性★

李 超， 王 斌

（湖南理工学院机械工程学院， 湖南 岳阳 414006）

连铸结晶器主要结构是由中间包、水口及结晶器组成，是整个连铸生产顺利完成的必要保证[1]，如图1 所示。结晶器主要作用是快速凝固铸坯，使铸坯凝固出一层薄壁，在出结晶器时具有一定力学性能，保证后续的轧制工序。当钢液在结晶器内凝固时，倘若出现偏析、内部裂纹等缺陷将永远保留在铸坯中，很难通过各种工艺手段去除，因此，结晶器是整个连铸过程的必要保证[2]。因此，研究结晶器内钢液的流动、凝固、传质成为了连铸结晶器冶金学的三大核心问题[3]。在所有的核心问题中，结晶器内流场形态是决定了铸坯凝固的快慢和铸坯内部质量缺陷的产生。为了防止出现质量缺陷，同时保证凝固速率，提高生产效率，分析结晶器内钢液的流动是捷径。因此，对连铸过程中结晶器内钢液流动现象的深入研究有助于优化连铸工艺和凝固过程提高铸坯的质量[4]。

图1 连铸结晶器

在学者们长期研究过程中，发现用实验方法研究结晶器钢液流动、凝固是存在一些问题的。而结晶器内流场的分析是研究的起步，关系到整个研究的准确性，所以数学建模及三维仿真成为研究钢液流场的有效方法。目前在流场模拟中比较流行的是大涡模拟(large eddy simulation, LES)方法[5]，其分析湍流的数据非常接近真实值，但大涡模拟对网格尺度的要求高，不仅在近壁区模拟时，其网格精密度要求很高，远壁端的精度也很高，提高了整个模拟数据量，因此大涡模拟目前还不太适合求解冶金湍流问题。Spalart 等人[6]在综合比较各种流场模拟方法之后，发现雷诺平均(Reynolds averaged Navie-Stokes,RANS)模拟适合于整个流场分布研究，网格尺度要求低，但对于壁面研究过于简化，使得精确度无法得到保证。所以，为了能够得到精确模拟结果，又希望可以简化数据量，提出一种新理念就是RANS/LES混合方法。构建一种新型数学模型，要适用于分离问题的计算，即在近壁端运用大涡模拟保证精度，远壁端运用雷诺平均降低数据量。

1 数学模型构建

1.1 RANS 与LES 方法的联立

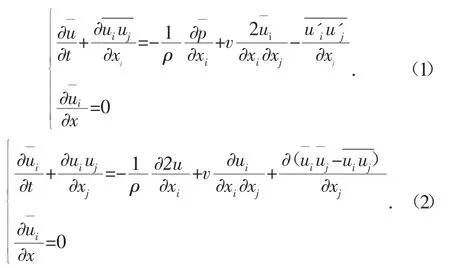
式（1）为RANS，式（2）为LES，从两式可以发现有类似的形式，即右端含有不封闭项为了将两式结合，可将此不封闭项采用动态Smagorinsky 模型表征出来：

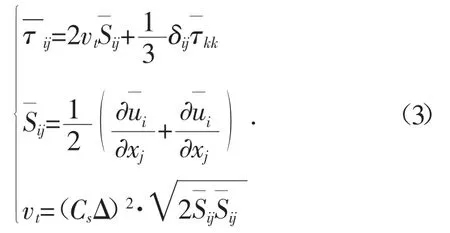
式（3）中Sij为尺度张量，Cs为模型系数，Δ 为网格尺度，νt涡粘系数。

1.2 基于双方程的大涡模拟方法

在雷诺平均模拟时，经常会涉及两个重要的脉动量参数，即湍动能k和湍流能耗散率ε。湍流应力就可以写成：

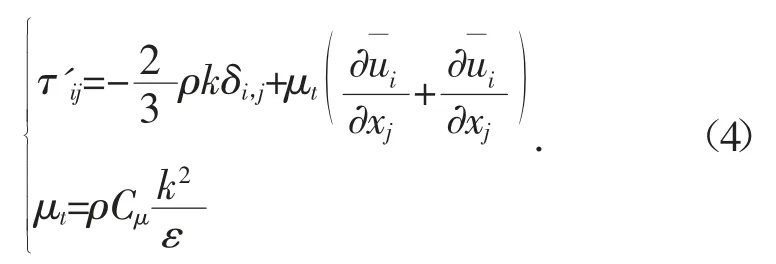
由公式（3）中νt涡粘系数与特征长度有关，因此需要在雷诺平均模拟中找到特征长度关系。此时，含能涡向小尺度涡的能量传递率等于ε，含能涡特征长度l=k3/2/ε，将其代入公式（4），将k方程中的ε 项替换，即：

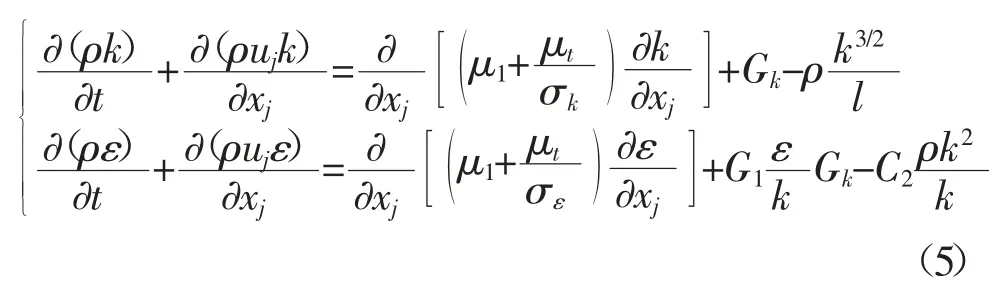
根据以上公式共同点联立，组合模型的框架自然产生了。基本思想是采用统一的涡粘运输方程，以网格分辨尺度区分RANS 和LES。特征长度为l¯=min（y，CΔ），其中y是网格点和壁面间垂直距离；Δ=max（Δx，Δy，Δz）是当时的网格尺寸最大值；C是常数，其标准值为0.65。在近壁区，特征长度与壁面成正比，即l=ky，k=4。替换y，则新长度尺度为l¯=min（k3/2/εk，CΔ）。当CΔ≥k3/2/ε 时，此时就是标准k-ε 双方程；而当CΔ＜k3/2/ε 时，l¯=CΔ，于是典型大涡模型出现了。在模拟平衡湍流或接近平衡湍流时，新数学模型采用标准双方程；处于非平衡的复杂湍流，新模型采用大涡模拟能更好解决问题。

2 数学模型的验证

2.1 计算参数设定

计算主要参数设定如下：选取铸坯的1/2 体积，网格总数设定约1.5×106，时间步长为0.000 1，计算时间为200 s。

2.2 边界条件

1）壁面。垂直于壁面的速度分量设为零，平行于壁面的速度、压力及、采用无滑移边界，即

2）初始速度。利用质量守恒确定倾角为θ 的水口出口处钢液速度ux，uy=ux·tanθ，uz=0。而kinlet=

3）结晶器出口。可采用无穷远出口边界条件，即所以物理量沿出口法线方向的梯度为零。

2.3 计算方法

采用基于双方程的大涡模拟数值方法，将上述微分方程离散成差分方程。流场的求解采用SIMPLE算法对压力连接性方程求解，离散后得到的代数方程采用TDMA 方法和Gauss-Siedel 方法进行计算。所有的计算结果均采用FORTRAN 语音编程。在计算中，收敛判断标准如下：

1）连续性方程中的质量源项的残差小于10-7。2）进出口流体流量差小于0.1%。

2.4 与经典模型算例比对

为了验证数学模型的正确性，与Thomas 等人设计的水模型结构参数进行模拟计算，并与文献[7]的PIV 测试结果进行比较，从图2 比较结果可以看出，计算结果和实验结果吻合度很好。由此可以说明，新构建的数学模型适用于结晶器内流场分析。

图2 经典模型比对

3 数值模拟及分析

对大断面连铸坯进行设计，分别模拟不同的浸入式水口开口、插入深度和拉坯速度，分析结晶器内钢液流动行为。

3.1 浸入式水口开口角度

结晶器内水口张角的变化直接影响钢液湍流上下回流区的位置，表面速度和壁面冲击力点。图3 所示，无论水口开口角度如何变化，越接近水口，结晶器表面波动速度先增大后减小，在浸入式水口距壁面中心位置附近，波动达到最大值。当侵入式水口开口由向下20°提升到向上20°时，流动形态没有明显变化，但是结晶器表面钢液的波动变大，在距中心位置附近达到最大值。向下20°时，最大液面流速为53 mm/s；而向上20°时，最大流速为66 mm/s，增大值为13 mm/s。如图4 所示，当浸入式水口开口为向下20°时，最大冲击力在结晶器液面下340 mm 处；而水口开口向上20°时，液面流速增大1.3 倍，最大冲击力在结晶器液面下300 mm。

图3 水口方向液面速度

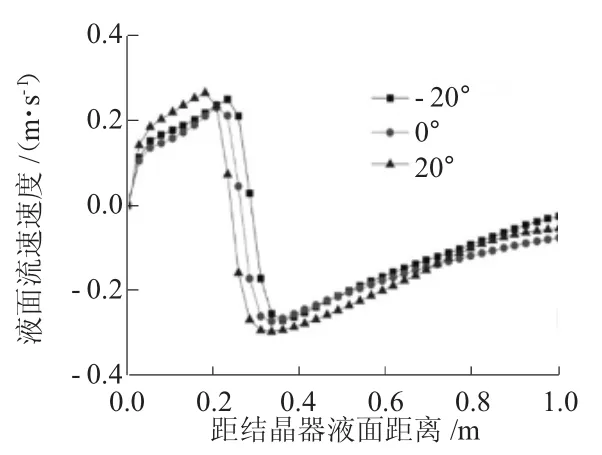
图4 结晶器壁面方向速度

3.2 拉坯速度

随着铸坯出结晶器的速度增加，从水口的钢液喷出速率也随之增加，当钢液喷出速率达到极限时，拉坯速度也就到达最大值。此时钢液流动获得最大的上升流股和下降流股的动能。如图5 所示，当出结晶器速度为0.6 m/min 时，结晶器液面最大流速为51 mm/s；而当拉坯速度为1.0 m/min 时，结晶器液面最大速度为73 mm/s，从而液面速度增大了1.56 倍。如图6 所示，随着铸坯出结晶器的速度增加，冲击强度增大，但是最大冲击点未有明显变化。

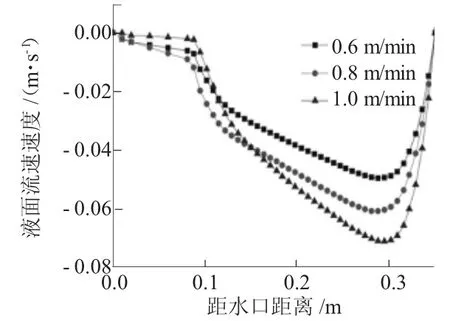
图5 水口方向液面速度

4 结论

1）由于结晶器内钢液湍流复杂且存在很多工艺参数影响，而钢液流动的数值分析准确性又决定了后续研究的走向，所以要针对结晶器冶金理论的特殊性，选择适合于结晶器内钢液流动理论方法。本文在研究结晶器内钢液流动特性时，采用基于双方程的大涡模拟数学模型，既保证了模拟的准确性，又满足计算量的适中要求。通过与经典模型算例对比，验证了新数学模型对于结晶器内钢液湍流的研究是可行的。

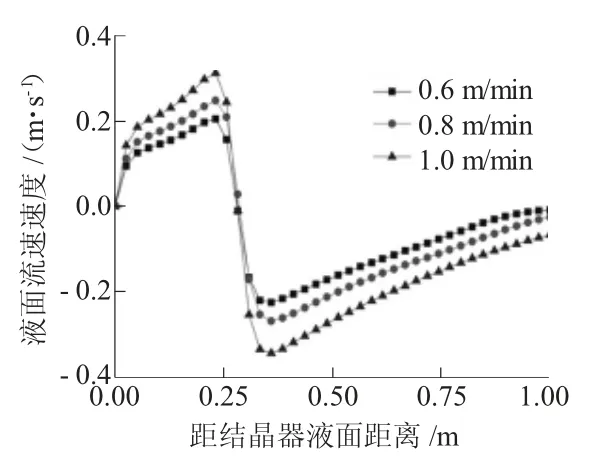
图6 结晶器壁面方向速度

2）不同工艺参数变化对结晶器内流场影响，当水口角度由下向上变化时，钢液冲击点上移，结晶器液面波动性加剧，这样有助于钢液中的夹杂物上浮；液面流速最大值增大，钢液流股对熔池表面冲击强度也随之加强，从而加剧了自由表面的波动和不稳定，容易造成钢液的二次氧化和保护渣的卷入。当拉坯速度的增加，加速了液面波动，易产生卷渣的倾向，虽然钢液股流的冲击点位置未变，但是冲击强度增加，造成初生坯壳减薄，强度降低，在浇注过程中漏钢的可能性增大。