读懂概念才是数学教学的核心

摘要:数学的概念教学不能流于表面,而应该抓住概念的核心,加上数学教材编排的特点是螺旋上升式,因此很多数学概念会在不同的学段重复出现,故如何把握这些概念的“度”是值得我们深入探讨的!
关键词:概念核心;解读;处理;完善
数学的概念教学不能流于表面,而应该抓住概念的核心,起始课时应当让学生明了概念的一般属性,而后续的学习则应当在起始课时的基础上,或是从抽象的角度,或是从概念核心的挖掘等方面进一步提升,因为这将关系到学生后续的学习,也关系到学生是否能灵活而准确地运用概念解决问题。小学数学教材(人教版)编排的特点是螺旋上升式,因此很多数学概念会在不同的学段重复出现,这些重复出现的数学概念在教学中应如何把握它的“度”?值得我们探讨!
一、 解读概念,认准认知起点
数学概念教学是数学教学内容之一。学生掌握数学概念,就可以形成对数学的基本的、概括性的认识。如果能使学生明确概念的内涵、外延,从而形成概念系统,那学生对于所学概念就有较为清晰的认识;如果学生再能了解概念的来龙去脉,能够正确运用概念,那学生对于所学概念就了然于心。如何能帮助学生达到“熟能生巧”地运用概念,首先我们教师就得对所教学的概念解读通透。
关于“轴对称”与“轴对称图形”这两个概念的认识应该要科学、客观,因为这两个概念既相互联系又有区别:“轴对称”讨论的是两个图形,两个图形沿着某一条直线的对称现象;而“轴对称图形”则考虑的是一个图形,图形自身沿某一条直线左右两边具有的对称现象。
关于“轴对称图形”的知识,学生在小学阶段会接触到两次:一次是二年级的“图形的运动(一)——认识轴对称图形”,一次是四年级下册“图形的运动(二)——轴对称”。本人认为:四年级下册“图形的运动(二)——轴对称”这一课内容的命名上值得商榷,因为小学阶段讨论的“轴对称图形”一般是基于一个图形自身的对称。其实对于“轴对称图形”,学生不需要老师教学,他们已经从生活中积累了大量的关于“对称”的认识和经验。“轴对称图形”在小学阶段是以一个图形本身的对称现象作为学习讨论的内容,那二年级、四年级,两个年级都出现轴对称图形的内容,这里面是否有什么联系和区别呢?答案是肯定的!二年级主要是借助生活中具体的物体感知轴对称这一几何现象,在仔细观察、反复对折的操作中,研究轴对称图形的对称性;而四年级则在课一开始着重介绍对称轴,让学生明白“对称轴”对于轴对称图形的重要性。接着借助方格纸,通过数格子发现轴对称图形的特征,以及如何借助方格纸补全一个轴对称图形,使得学生由直观观察判断转化为理性地借助对称点来判断、理解轴对称图形的特征。二年级时,对轴对称图形的判断方式比较单一,就是通过观察、对折操作,以“两边是否能够完全重合”来判断图形或物品是否对称;而四年级轴对称图形的判断方法则比较多样,除了观察、对折的方法外,还有更理性的判断方式:借助格子图,找到对应点到对称轴的距离是否相等的方法来判断,还可以借助想象来加以判断。
二、 合理处理,直观抽象关系
在小学阶段,学生接触的数学概念其实或多或少在生活中都有所接触,或只是流于表象,真正要学生用语言描述,大部分存在一定的困难。因此需要我们老师把孩子们眼中这个直观的物体,经过合理地引导,使得学生能用抽象的语言表达,甚至能抽象出这个概念的本质特征。
由于二年级已经有接触过轴对称图形,因此课一开始,就以几幅生活中常见的轴对称图片引入,接着课件呈现图形对折后两边完全重合的动态画面,使学生很自然地到已有认知系统中去搜索相关知识,以唤醒已有认知经验。但如果本节课一开始仍然停留在观察的直观层面上,忽略了学生已有的认知,则有些“炒冷饭”的嫌疑,因此引入环节,除了让学生直观的观察外,还应对学生提出“发现了什么”“什么是完全重合”等问题,引导学生用抽象语言把自己观察到的现象表达清楚。学生对于轴对称现象一般只停留在表面,大概地知道:兩边一样的图形是轴对称图形!学生如果一直停留在这个直观的层面上,不利于发展学生的思维,也不利于理解“轴对称图形”核心的特征。轴对称图形特征的本质在于“沿对称轴对折后,两边完全重合”!那为何轴对称图形沿着对称轴对折后,两边一定会完全重合呢?要解决这一困惑点,学生将会经历两次的由直观到抽象的转变:先借助直观操作、观察动态重合的物体,再用抽象的语言描述轴对称图形的特征;再借助直观的数格子,抽象出“对称点两边的格子数相等”来理解轴对称图形的本质特征——对称轴两边的对应点到对称轴的距离相等,这也是“为什么轴对称图形沿着对称轴对折后,两边图形能不多不少地重合在一起”的关键点。通过直观地观察到抽象语言表达这一步的转化,学生对于轴对称图形的特征有了进一步的认识;再由数格子到发现对应点到对称轴之间的距离相等,那么学生对于轴对称图形的特征才有了质的飞跃,这样才能让学生将“轴对称图形”这一概念真正读懂、读通、读透。
数学概念的教学亦是如此,通过几次“直观与抽象”地转化中,学生对所接触的概念有了进一步的认识,并逐步抽象内化,乃至对概念的本质属性有了深刻清晰的了解,至此概念教学才是完整呈现,而学生也能运用内化的概念知识进行变通运用。
三、 纠正完善,理解核心概念
我们数学语言讲究精确,对于概念的教学更是不能有丝毫的偏差。当学生认识出现偏差时,应积极引导学生纠偏纠错,通过判断、交流、讨论,不断地引导学生逼近正确结论。学生对于概念的认识,从来就不是一蹴而就的,一般要经过反复观察、对比、概括,才能逐步内化。学生在认识“什么是轴对称图形”中,学生往往会出现认识的误区:认为沿着对称轴,左右图形一样、大小相等就是轴对称图形,实则不然。
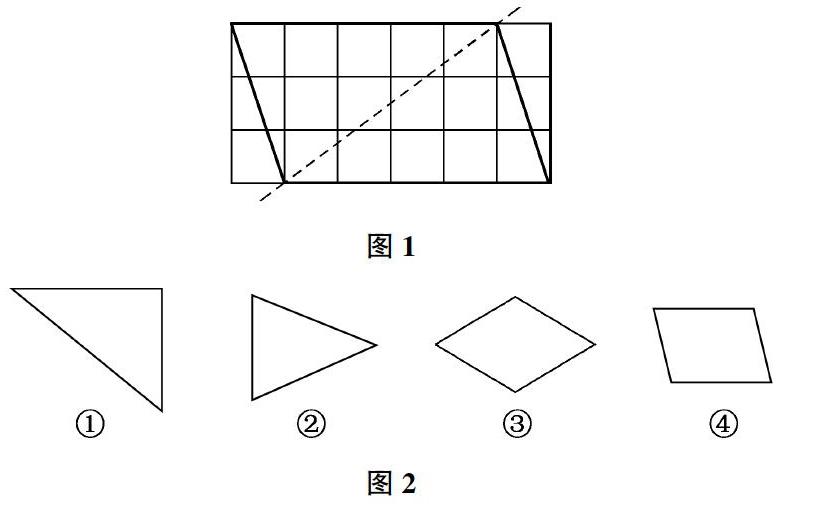
教学中,可以先让学生借助格子图补全轴对称图形的另一半,从而考查学生是否真的理解“轴对称图形中对应点到对称轴的距离相等”。接着让学生判断这些图形(如图1)是不是轴对称图形。学生对于前面3个图形都不会有什么异议,而事实证明正确率的确挺高的。但对于④号图形,大部分学生都认为这是一个轴对称图形,理由:因为沿着对角线一连接,分成两个同样大小的三角形(如图2)。这是因为学生对轴对称图形概念的认识出现问题:认为只要对称轴左右两边图形大小相等,就是轴对称图形。其实不然,应该是“沿着对称轴对折,两边完全重合”这才是轴对称图形的本质!这两个三角形虽然大小相等,但沿着对称轴对折,两边根本没法完全重合。这时考验我们老师对于概念钻研够不够深入,理解是否到位的时刻到了。在我们老师看来觉得很简单的概念,因而没能引导学生通过深入辨析,从而理解概念本质内涵,导致学生对于概念本质掌握不够深刻,因此练习中,无法推动学生进行深入的数学思考,从而无法做出正确的判断。对于四下“轴对称图形”的教学,掌握轴对称图形的特征是教学的重难点,学生只有真正理解了概念,才能在后续的练习中做出正确的判断。学生必须充分认识到:将一个图形平均分成两份,哪怕大小相等,形状相同,但只要沿着任意方向对折,都没法使左右两边图形完全重合的,就能判定该图形并不是轴对称图形。
这样在概念形成过程中,学生从感性到理性不断地感知并尝试表达,当发现理解有漏洞时,及时纠正弥补,从而提升学生思维的缜密性。
四、 合理设问,发展空间想象
概念教学不应只局限于本节概念课所呈现的内容,还应统观全局,从本节概念课隶属的教学模块的本质属性出发进行教学。轴对称图形在教学中,要求“依据语言描述出图形的特征”“物体运动变化反映在人的头脑里,形成有关的概念、模型”,这就是所谓的“空间观念”,空间观念其实它所表达的意义是多方面,但主要是以下两个方面:一方面表达的是对几何图形的操作实践,具有一定的直观操作性;另一方面表现的是图形的相关概念,具有一定的抽象思维性。如何在“轴对称图形”这节课中将“空间观念”所要表达的这两种特性完美地结合并呈现呢?基于对这个问题的思考,在教学设计时,我们提出这样的疑问:是否认识轴对称图形只能依赖对折?能否借助图形让学生在头脑中展开想象,想象对应点与对应线段的位置关系?
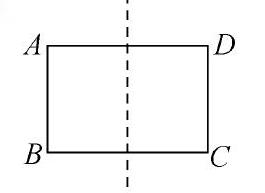
因此可以设置这样的问题(如右图):在长方形ABCD中,如果沿着这条对称轴对折,那么点A会跟哪个点重合?让学生对所观察到的图形在头脑中进行翻折、想象,并能从已经确定是轴对称图形的基础上,进一步想象出相应重合的点。使得学生对于结果的判断不仅仅只是依靠直觉,而是有了更具体的思维过程。还可以设置这样的问题(如下图),在正方形ABCD中,如果线段AC与CD重合,那么是沿着哪一条对称轴对折。这时,学生在头脑中对正方形的四条边,从各个方向进行翻折,想象怎样翻折才能使AC与CD这两条边“完全重合”。学生头脑中,一开始参与了想象、翻折活动等活动,他们的判断还会不太确定,因此还需要借助动画,或者动手实践才显得更可靠。但这样的几个回合后,学生就能在头脑中建立起较为丰富的、精准的轴对称图形的相关表象,从而促进学生相关空间观念的形成。
在概念教学中,教师应尽量通过“观察—操作—思考—想象”等一系列的过程,帮助学生由直观到抽象,逐步建立相关概念的表象,促进学生对所学概念所呈现的形式、关系有较深刻理解。
参考文献:
[1]张奠宙.小学数学教材中的大道理——核心概念的理解与呈现[M].上海教育出版社.
[2]小學数学教师.上海教育出版社,2018.10-2019.02.
作者简介:
陈彬燕,福建省厦门市,厦门外国语学校海沧附属学校。

