基于ARIMA模型的新冠肺炎序列分析预测
纪安之

摘要:利用国家卫生健康委公开的2020年1月24日24时至2020年3月29日24时新冠肺炎累计确诊病例数据,采用时间序列分析方法建立ARIMA模型进行拟合分析,并预测其未来走势。用 SAS软件编程,结果表明,原序列2阶差分后为平稳非白噪声序列,ARIMA(0,2,1)模型可以较好地拟合原序列,并通过了模型的显著性检验和参数的显著性检验。未来5日的预测结果与实际数据吻合较好。
关键词:新型冠状病毒肺炎;时间序列;ARIMA;预测;SAS
Abstract: Using the data of 2019-nCoV pneumonia cumulative diagnosis from 24:00 on January 24, 2020 to 24:00 on March 29, 2020, the ARIMA model was established by time series analysis to analyze the trend and predict the future trend. The results show that the original sequence is a stationary non white noise sequence after the second-order difference, ARIMA (0,2,1) model can fit the original sequence well and pass the significance test of the model and the significance test of the parameters. The predicted results in the next five days are in good agreement with the actual data.
Key words: 2019-nCoV;time series;ARIMA;prediction;SAS
1 绪论
2019年12月,新型冠状病毒肺炎在湖北省武汉市出现,并迅速蔓延至武汉市以外地区[1]。2020年1月12日世界卫生组织正式将造成武汉肺炎疫情的新型冠状病毒命名为“2019新型冠状病毒”(2019-nCoV)[2]。新型冠状病毒肺炎属于β属冠状病毒,人群普遍易感[3-4]。新冠肺炎疫情发生后,党中央高度重视,及时部署了防控措施:延长春节假期、延迟开学、灵活复工、错峰出行[5]。通过采取一系列防控措施,目前我国疫情防控形势持续向好,多省实现“零增长”,武汉疫情快速上升的态势也得到控制。
新型冠状病毒肺炎疫情是我国自新中国成立以来传播速度最快、感染范围最广、防控难度最大的一次重大突发公共卫生事件。截止3月29日24时,全国累计报告确诊81470例,累计治愈出院病例75770例,累计死亡病例3304例[6]。为进一步了解2019新型冠状病毒疫情的变化情况并预测其未来走势,现利用国家卫生健康委每日公开累计确诊病例数据,采用时间序列分析方法对2019新型冠状病毒病例数据进行分析。
2 方法
2.1 数据来源
本次研究选取的样本数据来源于国家卫生健康委自2020年1月24日24时至2020年3月29日24时的公开累计确诊病例数据,如表 1所示。
2.2 ARIMA模型
美国Wisconsin大学的Box和Jenkins提出的时间序列(Time-series Approach)分析方法中,求和自回归移动平均模型(Autoregressive Integrated Moving Average Model,简称ARIMA)是主要运用于分析非平稳的、不具有季节性变化趋势的时间序列[7]。ARIMA模型包括自回归(Auto Regressive,AR)模型,移动平均(Moving Average,MA)模型,或自回归移动平均模型(Auto Regressive Moving Average,ARMA)模型[8]几种特殊情况。
ARIMA(p,d,q)模型结构如下。其中p为自回归项数,q为移动平均项数,d为时间序列成为平稳时所做的差分次数[9]。
2.3 ARIMA模型建模步骤
①平穩性检验:根据观察值序列的时序图判断序列的平稳性。当时间序列呈周期性或者有显著趋势时,对原序列数据进行差分运算;
②白噪声检验:在检验的显著性水平取0.05的条件下,当延迟6阶的 检验统计量的P值小于0.05,则该差分序列不能视为白噪声序列;
③拟合ARMA模型:根据自相关图和偏自相关图的性质,选择阶数适当的ARMA(p.q)模型进行拟合;
④在条件最小二乘估计原理下估计模型中未知参数的值;
⑤对残差序列进行检验:当拟合检验统计量的P值都显著大于显著性水平0.05,则认为残差序列即为白噪声序列;如果拟合模型通不过检验,转向步骤②,重新选择模型再拟合;
⑥利用拟合模型,预测序列的将来走势。
3 建模及预测
3.1 平稳性检验
首先,绘制监测数据序列时序图,该序列时序图如图 1所示,新冠肺炎监测数据具有明显的持续增长趋势,为典型的非平稳序列。对原序列进行2阶差分运算提取数据序列中的确定性信息,如图 2所示,2阶差分后序列始终围绕在均值附近随机波动,即差分后序列没有显著非平稳特征。为了进一步确定平稳性,考察差分后的序列的自相关图,如图 3所示。自相关图显示序列具有很强的短期相关性。原序列2阶差分后序列平稳。
3.2 白噪声检验
对平稳的2阶差分序列进行白噪声检验,序列随机性检验结果如表 2所示。在检验的显著性水平取0.05的条件下,延迟6阶的x2检验统计量的P值为0.0333,小于?琢=0.05,可以以1-?琢的置信水平拒绝原假设,认为差分后序列蕴含很强的相关信息,所以该差分后序列为平稳非白噪声序列。
3.3 拟合ARMA模型
如图 3所示,综合2阶差分后序列的自相关图显示出自相关系数迅速衰减到零,自相关图呈现典型的1阶截尾性(q=1),而偏自相关系图显示出非截尾的性质,拟合模型定阶为MA(1)。原序列差分后平稳,差分次数为d=2,因此实际上是用ARIMA(0,2,1)模型拟合原序列。如表 3所示,运用条件最小二乘估计确定该模型的口径为:
3.4 模型检验
确定了拟合模型的口径之后,检验模型的显著性=0.05,检验结果如表 4所示。残差白噪声检验结果显示延迟6阶、12阶、18阶LB检验统计量的P值均显著大于0.05,认为拟合模型的残差序列通过白噪声检验,该ARIMA(0,2,1)模型显著有效。再检验参数的显著性0.05),检验结果如表4所示。均值MU的t检验统计量的P值为0.7894,大于=0.05,即均值MU不显著。
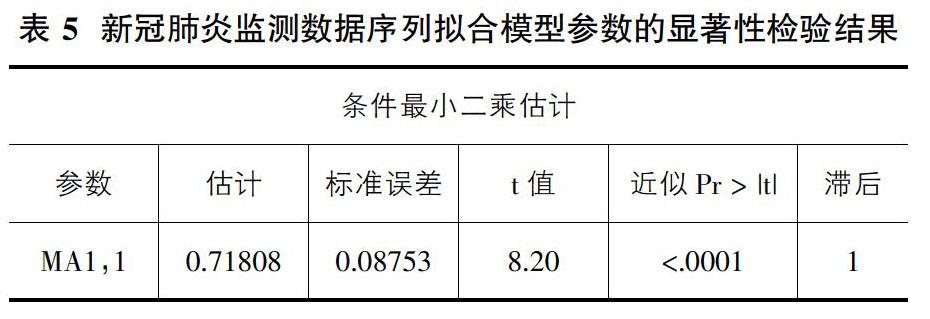
剔除常数项后重新拟合模型,再次估计模型中未知参数的结果,检验结果如表 5所示。参数MA1,1的t检验统计量的P值小于0.0001,认为该参数显著。因此,ARIMA(0,2,1)模型是该序列的有效拟合模型。
3.5 ARIMA模型预测
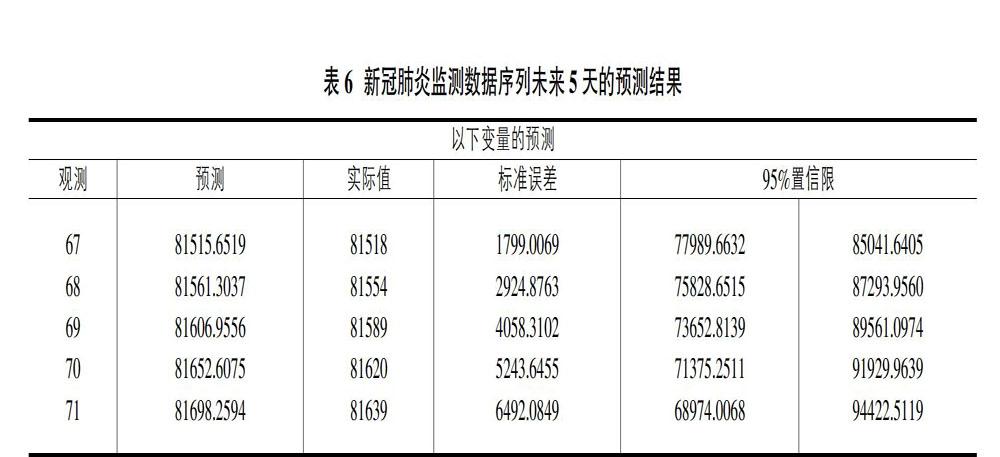
利用ARIMA(0,2,1)模型对新冠肺炎监测数据序列作5天预测。预测值、实际值、标准误差和95%的置信区间如表3-表5所示。从预测结果(表6)来看,预测数据和实际数据吻合较好。
4 结论
综上所述,ARIMA(0,2,1)模型对我国新型冠状病毒疫情走势具有较高的拟合度,可用于新冠肺炎监测数据序列的短期预测,可为疫情的防控效果以及发展趋势提供参考,为未来几天的疫情干预决策提供一定的政策依据。
参考文献:
[1]中国疾病预防控制中心新型冠状病毒肺炎应急响应机制流行病学组.新型冠状病毒肺炎流行病学特征分析[J].中华流行病学杂志,2020,41(2):145-151.
[2]世界卫生组织将新型冠状病毒感染的肺炎命名为“Cov-id-19”[ER/OL].(2020-02-11)[2020-02-21].http://WWW.xinhuanet.com//world/2020-02/11/c_1125561343.htm.
[3]国家衛生健康委员会老龄司.关于做好老年人新型冠状病毒感染肺炎疫情防控工作的通知[ER/OL].(2020-01-31)[2020-02-22].http://www.nhc.gov.cn/lljks/tggg/202001/96e82ba8a14d41b283da990d39771493.shtml.
[4]国家卫生健康委员会妇幼保健司.关于做好儿童和孕产妇新型冠状病毒感染的肺炎疫情防控工作的通知[ER/OL].(2020-02-02)[2020-02-22]http://WWW.nhc.gov.cn/fys/s7902/202002/de2d62a5711c41ef9b2c.4b6f4d1f2136.shtml.
[5]国务院办公厅.国务院办公厅关于延长2020年春节假期的通知[EB/OL].[2020-01-27].http://www.gov.cn/zhengce/content/2020-01/27/content_5472352.htm.
[6]国家卫生健康委员会官方网站.截至3月29日24时新型冠状病毒肺炎疫情最新情况[EB/OL].[2020-03-30].http://www.nhc.gov.cn/xcs/y qtb/202 003/c46e73d692d047619bfb29680950d88d.shtml.
[7]孟凡东,吴迪,隋承光.2004-2015年中国狂犬病发病数据ARIMA乘积季节模型的建立及预测[J].中国卫生统计,2016,33(3):389-391.
[8]张美英,何杰.时间序列预测模型研究综述[J].数学的实践与认识,2011,41(18):189-195.
[9]王燕.应用时间序列分析[M].四版.北京:中国人民出版社,2015:1-127.

