改进的SURF算法在图像匹配中的应用

黄春凤 刘守山 别治峰 许广会

摘  要： 针对加速稳健特征（Speeded Up Robust Features，SURF）算法在三维重建中匹配准确率低的问题，提出基于SURF算法的改进算法。首先利用SURF算法提取特征点，通过近邻搜索（Best Bin Fast，BBF）算法实现Kd?Tree快速查找最近邻特征点，结合双向唯一性匹配的方法完成图像匹配，然后在视差约束下，利用视差梯度约束对初始特征匹配对进行预处理，筛选掉一些偏差较大的匹配对，最后采用随机抽样一致（Random Sample Consensus，RANSAC）算法对特征点二次优化和去噪处理。将其他改进算法和提出的改进算法分别进行图像匹配处理比较，分析算法的性能，得到提出的改进算法匹配成功率达96.3%。实验结果证明提出的改进算法简单快速，匹配精度高。

关键词： 图像匹配; 特征点提取; 双向匹配; 视差梯度; 随机抽样一致; 匹配精度

中图分类号： TN911.73?34; TP391.9              文献标识码： A                     文章编号： 1004?373X（2020）10?0111?05

Application of improved SURF algorithm in image matching

HUANG Chunfeng， LIU Shoushan， BIE Zhifeng， XU Guanghui

（College of Electronic Information Engineering， Shandong University of Science and Technology， Qingdao 266590， China）

Abstract： An improved algorithm based on SURF algorithm is proposed to improve the matching accuracy of SURF （speeded up robust features） algorithm in three?dimensional reconstruction. The feature points are extracted by means of the SURF algorithm， Kd?Tree searches the nearest neighbor feature points quickly by means of BBF （best bin fast） algorithm， and then the image matching is completed in combination with the biuniqueness matching method. Under the disparity constraint， the initial feature matching pairs are preprocessed by means of the disparity gradient constraint， some matching pairs with large deviation are screened out， and the quadratic optimization and de?noising processing of feature points are carried out by means of RANSAC （random sample consensus） algorithm. The performance of other improved algorithms and the proposed improved algorithm were compared and analyzed respectively for image matching， from which the matching success rate of the proposed improved algorithm is 96.3%. The experimental results show that the proposed improved algorithm is simple， fast and has high matching accuracy.

Keywords： image matching; feature point extraction; bidirectional matching; disparity gradient; random sample consistency; matching precision

0  引言

近年来，随着科技的进步，双目立体视觉[1]技术被广泛应用，例如图像检索[2]、三维重建[3]、目标识别[4]、图像配准[5]等。其中，特征点检测与匹配作为双目立体视觉技术中的关键一步，显得尤为重要。常见的适用于特征匹配的算法中，较为成熟的有SIFT算法和SURF算法。SIFT算法[6]具有尺度不变性和旋转不变性，图像在尺度变化和旋转变化的情况下匹配效果受影响很小，由于采用差分高斯金字塔[7?8]进行特征点[7，9]提取，所以算法运行时间相应增加，降低了运行速度。1999年David Lowe提出了SURF[10]算法，由于SURF算法采用积分图像[11]、Harr小波变换[12]和近似Hessian矩阵[10]来提高速率，增加算法鲁棒性，所以相比SIFT算法，SURF算法运行速率快，鲁棒性强。但在求主方向过程中依赖局部梯度区域像素程度较大，匹配成功率并没有达到理想的效果，匹配精确度偏低。

本文首先在SURF算法的基础上通过BBF算法实现Kd?Tree快速查找最近邻特征点，结合双向唯一性匹配的方法完成图像匹配，然后在RANSAC算法之前利用视差梯度[13]约束对提取的特征点预处理，剔除大部分错误特征点，减少RANSAC算法计算量，对匹配结果中仍存在的偏差较大的伪匹配点，最后利用RANSAC算法进行二次优化和去噪处理。实验结果证明，该方法简单快速，图像匹配成功率高。

1  SURF算法原理与分析

1.1  提取特征点

Hessian[10]矩阵是SURF算法提取特征点的核心步骤，可以理解为一个多元函数在某一点处的二次偏导构成的方阵，是泰勒展开式的矩阵形式。对于一个图像中的点P=（x，y），尺度为[σ]的矩阵[H（X，σ）]定义为：

[H（X，σ）=Lxx（X，σ）Lxy（X，σ）Lxy（X，σ）Lyy（X，σ）] （1）

式中：[Lxx]指高斯滤波二阶微分，即[?2y?2xg（σ）]与像素点P = （x，y）的卷积，其中[g（σ）=12πσ2e-x2+y22σ2];类似地，[Lxy]和[Lyy]表 示[g（σ）]在各个方向的二阶微分与像素点P = （x，y）的卷积。

通过盒子滤波运算，进一步求得矩阵H的判别式：

[det（Happ）=LxxLxy-（0.9Lxy）2] （2）

1.2  特征点描述

通过在圆形邻域内计算特征点的Harr小波响应确定特征点的主方向。把与主方向水平的Haar小波响应称为[dx]，垂直方向的称为[dy]。通过计算[dx]，[dy] ， [|dx|] ， [|dy|]得到每个子区域的4个特征向量，则四维描述向量[Vden=dx，dy，|dx|，|dy|]，计算所有的4×4个矩形区域块，一共得到4×（4×4）=64维向量。

1.3  特征点匹配

采用欧氏距离的方法进行特征点匹配，针对一幅图像中的某一个特征点，在另一幅图像中搜索出两个距离它最近的特征点。在这两个特征点中，如果最近的距离[r1]除以次近的距离[r2]小于设定的阈值[14]P，则表示这两个特征点匹配度好，可以作为匹配点，否则抛弃。

1.4  SURF算法的图像匹配结果分析

根据以上所述过程，利用SURF算法进行图像匹配，匹配结果如图1所示。从匹配结果来看，图像中匹配对较多，并且含有大量錯误匹配对，匹配正确率低。针对此种情况，本文对SURF算法做了一系列改进。

2  改进的匹配算法

本文对SURF算法进行改进，基于改进的SURF算法系统框图如图2所示。

2.1  双向匹配算法

SURF算法配合双向匹配算法完成图像匹配，并初步筛选错误匹配点，匹配过程中需要处理的数据量巨大，Kd?Tree在维数较多的情况下，运行速率会大幅度降低，为了提高匹配速度，结合BBF算法实现Kd?Tree快速检索符合条件的特征点，完成双向SURF算法匹配。

假设有两幅待匹配图像，分别为图像1、图像2。采用双向匹配的方法改进SURF算法，增加了匹配结果的可靠性，目的是使图像1中的特征点唯一对应图像2中某个特征点，同时图像2中的特征点唯一对应图像1中某个特征点。原始的SURF算法匹配过程是以两幅图像中的一幅作为基准图像，在另一幅图像中寻找其对应的特征点，完成图像匹配。双向匹配算法在此基础上增加了相反方向的单向匹配过程。具体步骤是：首先把图像1作为基准图像，针对已经提取的图像1中的所有特征点，利用SURF算法中采用欧氏距离实现匹配的方法，通过BBF算法实现Kd?Tree快速检索特征点，在图像2中找到与之对应的特征点，匹配结果如图3a）所示;然后把图像2反过来作为基准图像，通过相同的方法，在图像1中找到与之对应的特征点，匹配结果如图3b）所示。采用运行在SURF算法之后的双向匹配算法初步消除SURF算法匹配结果中的部分歧义匹配点和伪匹配点，参照图3，双向匹配过后图像中仍含有错误匹配点，需要进一步剔除。

2.2  改进的RANSAC算法优化处理

2.2.1  RANSAC算法

通过RANSAC算法过滤误匹配，首先要求出一个最佳单应矩阵，将此矩阵记作H，H矩阵如式（1）所示，大小为3×3。为了找到最佳参数矩阵，最佳参数矩阵是指满足此矩阵的匹配点数量最多的矩阵，一般设定[h33=1]，目的是使矩阵归一化。参数线性方程如下：

[sx′y′1=h11h12h13h21h22h23h31h32h33xy1] （3）

式中：坐标（x，y）表示目标图像的角点位置;坐标（[x′]，[y′]）表示场景图像的角点位置;s为尺度参数。

2.2.2  基于视差梯度约束的RANSAC算法

引入视差梯度定义[14]，假如在一幅图像中存在两个相邻的角点p，q，这两个角点分别匹配于另一幅图像中的角点[p′]，[q′]，如果它们是相匹配的，那么视差梯度[Gd]应该小于或者等于2。如果视差梯度大于2，那么就可以认为这两个角点不是匹配角点。视差梯度的公式定义为：

[Gd=（p′-p）-（q′-q）（p′-p）+（q′-q）] （4）

式中：坐标[（p′，p）]和坐标[（q′，q）]是对应角点的图像坐标向量;[m]示向量[m]的模。

综合以上对视差梯度概念的理解和分析，改进的RANSAC算法流程如下所述：

1） 设定抽样数量为M，根据置信概率公式[P=1-（（1-ε）m）M]，计算出抽样数量M。其中[ε]代表数据错误率，m代表求解模型参数所需要的最小数据量，P指置信概率，一般取P=0.995。

2） 從所有匹配点中随机抽取匹配点作为一个抽样，每个抽样中含有m个数据样本。

3） 根据视差梯度定义，从所取匹配点中选出两对匹配点计算其视差梯度，若计算结果显示不匹配，则重新选择抽样样本，重新进行步骤2）;若计算结果显示匹配，则计算此抽样的模型参数。

4） 把该模型参数代入模型以过滤伪匹配点，通过相同的方法筛选M中其余的抽样样本。

5） 比较每组抽样得到的正确匹配点数量及误差方差的大小，选出匹配点质量最好的一组，以该组抽样获得的模型参数作为最佳模型参数，用最佳模型参数淘汰伪匹配点，得到正确率较高的匹配对，并用这些匹配对计算最终的模型参数。

3  实验结果分析与对比

本文所有实验均在Visual Studio 2015_OpenCV 3.0软件环境中编译完成，本实验所用图片均为WAT2200双目摄像头拍摄，计算机安装系统为Windows 10，型号为联想Idea Pad Y485。为了证明本文提出的算法比原始SURF算法更加精确高效，将SURF算法与本文改进的算法在光照、旋转等不同状态下分别做了对比，实验结果如图4所示。

图4a）和图4b）是双目摄像头采集的左右两张待匹配图像，图5a）、图5b），图6a）、图6b）和图7a）、图7b）分别为两种算法在三种不同状态下的匹配结果图。为了避免其他外在因素使比较结果产生误差，本文选用同一个物体拍摄的两幅图像进行不同程度的处理。待匹配图像为校准图像，所有匹配结果图中横线表示正确匹配对，斜线表示错误匹配对。图5～图7中，图a）为SURF算法匹配结果图，图b）为本文算法匹配结果图。

图5a）、图5b）是SURF算法和改进算法分别在正常状态下图像匹配的结果图，SURF算法匹配结果中匹配对较多，并且含有大量错误匹配对;改进算法的匹配结果中基本不含错误匹配对，或者说没有肉眼可见的错误匹配对，匹配精度高。图6a）、图6b）是两种算法分别在光照条件下对图像处理的结果图（受光照影响，图片颜色相对较浅），SURF算法受光照影响较小，匹配结果中仍然含有大量误匹配;改进算法匹配结果依然准确，没有发现受光照影响，鲁棒性强。图7a）、图7b）为两种算法分别在旋转状态下对图像处理的结果图，显而易见，改进算法的匹配结果没有受到图像旋转的影响，几乎没有发现伪匹配对。

从以上3组实验结果可知，SURF算法的匹配结果中匹配对相对较多，含有大量错误匹配对，匹配精度低;本文所提出的算法在匹配过程中剔除了较多的错误匹配点，匹配成功率高，并且不受旋转和光照因素的影响，鲁棒性强，大大提高了图像的匹配精准度。

在实验过程中，记录原始SURF算法和改进算法的运行时间和特征点个数，具体数据如表1和表2所示。表1记录了两种算法的正确匹配对数和错误匹配对数，表2记录了两种算法的正确率和运行时间。表1和表2表明，本文提出的算法在精确度方面优于原始的SURF算法，提高了图像的匹配正确率，运算速度并没有明显降低，基本和原始SURF算法相持平，因此，改进后的算法能更好地满足图像匹配需求。

使用SURF算法和改进算法分别在正常状态、光照和旋转条件下进行图像匹配测试，平均阈值P=0.9，阈值测试如表3所示。

为了进一步验证本文改进算法的可行性，将本文改进算法与其他改进的SURF算法作比较。采用FAST?SURF[15]算法、SURF?RANSAC算法和本文算法分别进行图像匹配，三种算法匹配结果图如图8所示。

利用FAST?SURF算法进行图像匹配时，首先通过FAST角点检测算法[15]提取特征点，通过非最大值抑制筛选特征点，检测到的特征点质量相对较高，然后通过SURF算法实现图像匹配，匹配结果较好。SURF?RANSAC算法在执行时首先通过SURF算法完成图像匹配，然后利用RANSAC算法剔除错误匹配对，实验过程中含有较多特征点，增加了RANSAC算法的采样次数，算法耗时稍长，匹配结果较好。

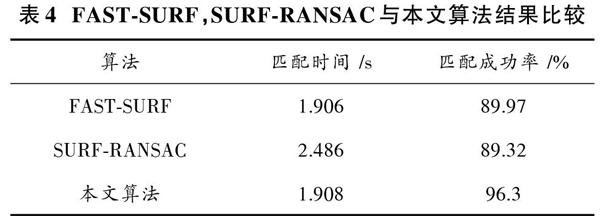
通过以上三种算法的匹配结果图可知，FAST?SURF算法和SURF?RANSAC算法总体匹配结果较好，含有轻微的错误匹配，匹配成功率比本文提出的改进算法低，具体实验数据如表4所示。

图9为三种算法在光照和旋转变化状态下的匹配正确率情况，可以看出三种改进算法在光照和旋转变化状态下匹配成功率都具有较强的鲁棒性，本文改进的算法匹配成功率高于其他两种改进算法。

4  结  语

本文实现了一种双向SURF算法，并结合改进的基于视差梯度约束的RANSAC算法剔除错误匹配对，使用改进的RANSAC算法加快原始RANSAC算法的运行速度，针对SURF算法匹配正确率低的问题做了深入改进。通过实验仿真与其他改进的SURF算法比较证明了该算法简单高效，大大提高了SURF算法的匹配精准度，弥补了SURF算法存在的匹配精度低的缺陷，具备一定的实用性。

参考文献

[1] ZHAO Sizeng， KANG Fei， LI Junjie. Displacement monitoring for slope stability evaluation based on binocular vision systems [J]. Optik， 2018： 171.

[2] Han Lina. Research on image fast retrieval application based on Bayesian network in hybrid space [C]// Proceedings of 2018 International Conference on Big Data and Artificial Intelligence. Beijing： ACM， 2018： 4.

[3] ZAVALA J P， GONZALEZ G， CASTILLO E， et al. Three?dimensional reconstruction of objects obtained by two orthogonal cameras [J]. IEEE Latin America transactions， 2015， 13（9）： 3162?3168.

[4] 邹浩，林赟，洪文.基于多角度合成SAR图像的目标识别性能分析[J].中国科学院大学学报，2019（2）：226?234.

[5] 赵杰，徐晓莹，刘敬，等.变参数active demons算法下的多通道弥散张量图像配准[J].中国图象图形学报，2019，24（1）：103?114.

[6] LOWE D G. Distinctive image features from scale?invariant key?points [J]. International journal of computer vision， 2004， 60（2）： 91?110.

[7] WANG M， YANG K Y， HUA X S， et al. Towards a relevant and diverse search of social images [J]. IEEE transaction on multimedia， 2010， 12（8）： 829?842.

[8] LOWE D G. Object recognition from local scale ?invariant features [C]// International Conference on Computer Vision. Corfu， Greece： IEEE， 1999： 1150?1157.

[9] ATEFEH Goshvarpour， ATAOLLAH Abbasi， ATEKE Goshvarpour. An accurate emotion recognition system using ECG and GSR signals and matching pursuit method [J]. Biomedical journal， 2018， 40（6）： 355.

[10] BAY H， ESS A， TUYTELAARS T， et al. Speed?up robust features （SURF） [J]. Computer vision and image understanding， 2008， 110（3）： 346?359.

[11] VOURVOULAKIS J， KALOMIROS J， LYGOURAS J. FPGA accelerator for real?time SIFT matching with RANSAC support [J]. Microprocessors & microsystems， 2017， 49： 105?116.

[12] 李颖桃，续欣莹，谢珺，等.一种基于邻域粗糙集特征选择的图像分类方法[J].现代电子技术，2019，42（8）：97?101.

[13] XU Wei， ZHANG Maojun， XIONG Zhihui， et al. Feature point matching based on bidirectional maximal correlation and parallactic restriction [J]. Computer engineering and applications， 2008， 44（28）： 155?157.

[14] 张杰，张末含，李述特，等.基于图像处理的橡胶树割痕提取与死皮识别[J].计算机应用与软件，2019，36（1）：259?262.

[15] 陈智翔，吴黎明，高世平.基于FAST?SURF算法的移动增强现实跟踪技术[J].計算机与现代化，2013（9）：105?108.