加密算法对GIF文件压缩率的影响
李 涛, 杜宝祥, 梁晓雯
(黑龙江大学 电子工程学院,哈尔滨 150080)
0 引 言
目前人们的沟通交流方式趋向于多元化,其中GIF文件作为一种动画媒体丰富了交流的方式。GIF文件同时具有占用资源小和表达信息丰富的特点,受到了大众的青睐。而GIF文件在传输和存储的过程中安全性容易受到威胁。GIF文件使用LZW压缩编码算法,许多专家学者基于LZW压缩编码算法提出一些高安全性的加密算法。Rajeev K等[1]提出一种基于LZW压缩编码的高容量可逆数据隐藏方案,该方案通过修改MTF编码技术来隐藏秘密数据,并增加了覆盖媒体元素之间的相似性。利用LZW编码技术对生成的覆盖数据进行LZW编码,以隐藏更多的秘密数据,提高了数据的加密安全性。Aruna M等[2]提出一种基于LZW压缩技术和彩色编码技术的大容量数据的加密方案。该技术利用转发邮件平台隐藏秘密数据。该算法首先对秘密数据进行压缩,然后将压缩后的秘密数据隐藏在邮件地址和邮件封面信息中。通过使用颜色编码表使消息着色,秘密数据位嵌入到消息(或覆盖文本)中。赵文强等[3]提出一种基于改进的LZW可逆数据隐藏方案,通过增加用于隐藏秘密的符号数量,提高隐藏速度和提取速度,从而达到更好的隐藏效果。这些加密算法的提出为数据的安全性提供了保障,但提高信息安全性忽略了加密算法对数据压缩率的影响。通过对比几种加密算法,分析不同加密算法对以LZW压缩算法作为压缩方式的GIF文件压缩率的影响。
1 知识背景
1.1 Arnold算法
Arnold变换。该变换的本质操作是拉伸和折叠,通过这两种操作可以改变图像内各像素点的空间位置[4],破坏像素点之间原来的关联,降低像素点之间的关联性。可用于视频图像加密中对视频图像进行位置置乱操作以达到对视频图像加密的效果。算法公式为:
(1)
式中,xn和yn分别为二维坐标系中某一像素点所在行和列的坐标;xn+1和yn+1分别为该像素点经过Arnold矩阵变换后所置换到新位置的行和列的坐标;mod为取余运算;N代表数据变换的维数,当Arnold加密算法用在图像处理领域时,N代表被处理图片的行和列的个数,Arnold加密算法只能用来处理行和列相等的图片;a、b取不同的值可得到不同的Arnold变换矩阵。a、b的值可以作为Arnold加密算法的秘钥,使用不同的a、b值生成多个Arnold变换矩阵处理视频的不同帧图像,可以提高视频信息的安全性。
1.2 Logistic算法
由于Logistic混沌系统具有出色的混沌特性,其被广泛应用在多媒体加密领域[5],该算法来源于虫口模型,其算法公式为:
xn+1=μxn
(2)
式中,xn为当前这一代虫子的数量;xn+1为下一代的虫子的数量。第n代虫子的数量是第一代虫子数量的μn-1倍,显然该增长不符合自然规律。经过研究后提出一种更合理的Logistic算法,算法公式为:
xn+1=μxn(1-xn)
(3)
当μ的取值在(3.569 945 672…,4)之间时,此式对初值敏感、不具有周期性、有奇异吸引子,而这些特性正是混沌系统所特有的[6]。
1.3 约瑟夫置乱
约瑟夫置乱加密的原理是使用约瑟夫环将数据进行重新排列。约瑟夫环是一个数学应用问题,过程为N个人围着一个圆桌,对这N个人用1,2,3,…,N进行标记,设定从第a个人开始从1数数,数b个数并将此人移出,他的下一个人从1开始标记,并从第a个人开始从1开始数数,数到b个数的人移出,依次按照该移出规则,直到将圆桌上的最后一个人移出后则游戏结束[7]。利用该移出规则按照移出的顺序对此N个人进行重新排序就是约瑟夫置乱算法。
1.4 GIF文件和LZW压缩编码
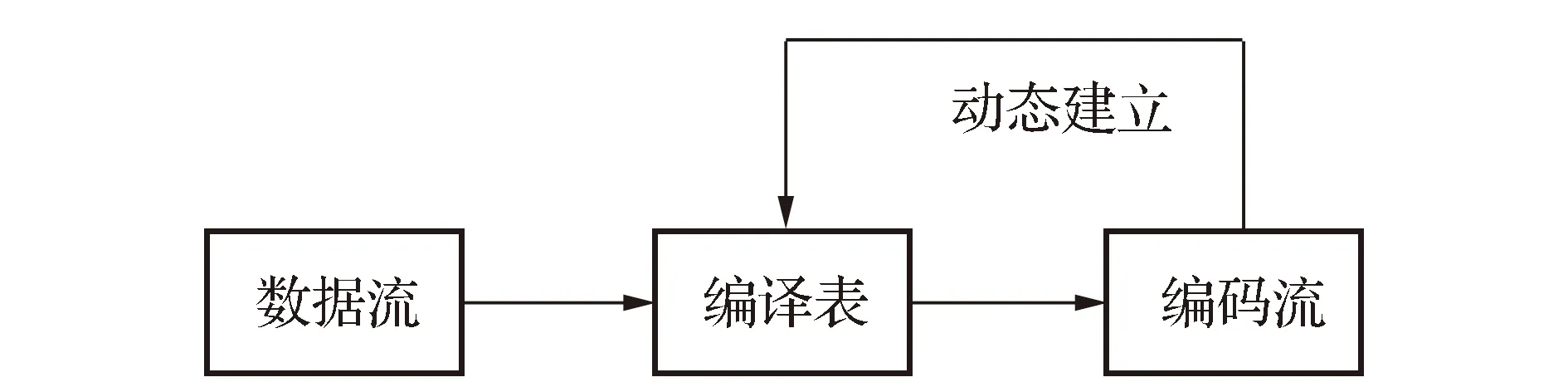
图1 LZW压缩编码过程图Fig.1 LZW compression coding process diagram
GIF是“图像交换格式”,可以通过将多幅彩色图像连续播放形成动画,其具有时间短、体积小、内容简单、成像相对清晰等特点。GIF是一种动态图像媒体。GIF文件被广泛应用于日常交流中,可以增添交流中的趣味性,方便日常沟通。
GIF动图具备帧间相关性大的特点,多采用LZW压缩编码。LZW压缩编码又叫“串表压缩算法”,它通过建立一个字符串表,用较短的代码来表示较长的字符串来实现压缩。它是对数据流压缩编码的同时进行编译表的扩充编写,即编译表不是在压缩编码前就建立完成的,而是根据原始文件动态建立。LZW的编码过程见图1。
LZW压缩编码算法中的核心内容是编译表的动态建立过程,在编码前首先建立预定义编译表,如用数字“1”表示字符“A”,用数字“2”表示字符“B”,用数字“3”表示字符“C”……则预定义的编译表中建立了26个相互映射的规则。在编码过程中根据输入的数据流及编译表中已存在的编译规则对编译表进行扩展,即为编译表的动态建立。如对字符串“TOBEORNOTTOBE ORTOBEORNOT”。若对该字符串使用预定义的编译表进行编码,则需要使用24个编码单元,即每一个字符使用一个编码单元进行编码,而使用LZW压缩编码算法对该字符串进行编码,仅需要16个编码单元即可完成编码,在存储和传输的过程占用的资源相对较少。对字符串“TOBEORNOTTOBEORTOBEORNOT”编码的过程建立的编译表见表1。通过该例说明,LZW压缩编码算法对相关性较高的数据压缩效果更好,适合被应用于GIF文件压缩。

表1 动态建立的编译表Table 1 Dynamically created and compiled tables
2 加密算法对压缩率的影响
为测试使用不同加密方案对GIF文件压缩率的影响,使用不同的加密方案对同一个GIF文件进行加密操作,并测试加密后密文帧间图像的相关性。明文GIF文件分离的彩色图像分辨率为500×500,GIF分离的彩色图像见图2。

图2 GIF文件帧图像提取Fig.2 GIF file frame image extraction
使用Logistic算法产生混沌序列与明文数据异或加密;使用Arnold算法对图像像素位置置乱加密,每帧图片的加密秘钥不同;使用约瑟夫算法对图像使用位置置乱的方式加密。3种加密方式的加密流程见图3。使用不同加密算法对由GIF文件分解生成的一组图片加密后相邻帧间相关系数的测试见图4。
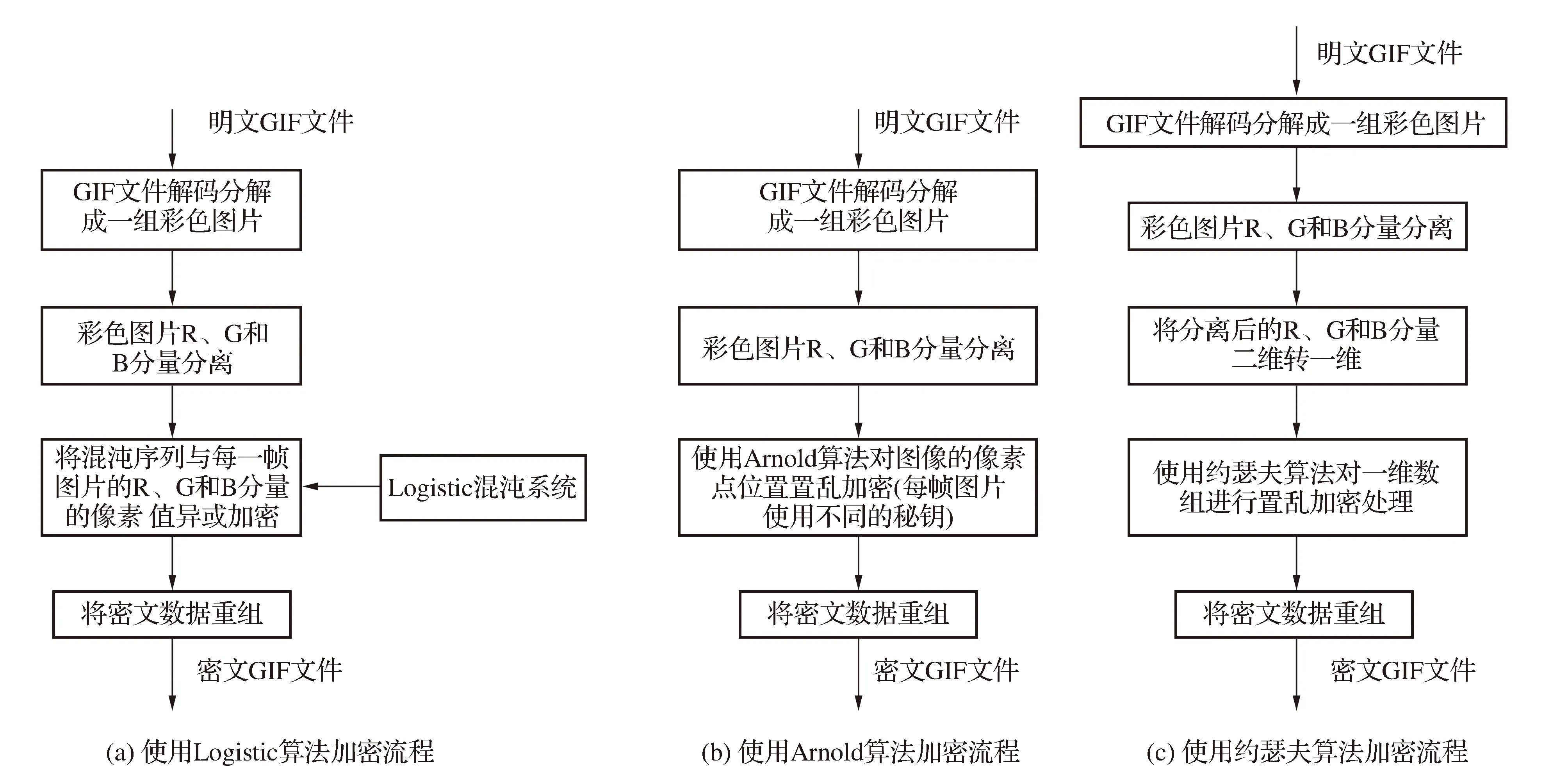
图3 不同加密算法加密流程Fig.3 Encryption flow chart of different encryption algorithms
由图4可见,使用Logistic算法加密后的GIF文件相关系数较原文件降低,使用Arnold算法加密后的GIF文件相关系数较原文件提高,而使用约瑟夫算法对图像使用位置置乱的方式加密,相关系数不变。
为进一步研究使用不同加密算法对压缩率的影响,对加密后的图像使用LZW压缩编码算法编码重组GIF文件,并计算文件大小。使用不同加密算法加密后图像重组GIF文件的大小见表2。

图4 不同加密算法加密后相邻帧间相关系数Fig.4 Correlation coefficient between adjacent frames after encryption by different encryption algorithms

表2 不同加密算法加密图像重组GIF文件大小Table 2 Image recombination GIF file sizes encrypted by different encryption algorithms
由图4及表2可见,使用Logistic加密算法得到的相邻帧间相关系数较原文件低,重组的GIF文件占用内存较原文件大;使用Arnold加密算法得到的相邻帧间相关系性提高,重组后的GIF文件占用内存较原文件小;使用约瑟夫加密算法得到的相邻帧间相关系数和重组GIF文件的大小不变。
3 结 论
通过分析及实验证明,不同加密算法对GIF文件的压缩率有不同的影响。在使用加密算法对文件加密提高文件安全性的同时,无论采用何种文件压缩算法,都需要考虑文件在传输和存储过程中的资源占用问题,有利于促进万物互联时代的发展。

