基坑开挖诱发既有建(构)筑物变形的SVM-BP预测模型及其工程应用
李立云,孙庆玺
(北京工业大学城市与工程安全减灾教育部重点实验室,北京 100124)
0 引言
基坑开挖会改变基坑周边岩土体的应力状态,从而导致其发生形变。 过大的场地变形将会对基坑周边建(构)筑物的安全造成很大影响[1]。图1 揭示了基坑开挖诱发周边场地产生不均匀沉降,致使周边建筑物发生侧倾进而可能破坏的现象。 因此,基坑开挖过程中周边建(构)筑物的安全是工程界的关注热点。 为此,及时准确地获取基坑周边建(构)筑物的沉降变形情况,构建有效的评价体系是问题研究的关键。

图1 基坑开挖后周边建筑物的变形情况Fig.1 Deformation of surrounding buildings after excavation of foundation pit
在建(构)筑物沉降变形指标获取方面,根据建(构)筑物的特点选择监测项目,在关键部位布设监测点,实时监测基坑开挖过程中这些监测点的数值变化是最为直接和有效的手段。 寻求高效的基坑周边建(构)筑物沉降的预测方法已是研究热点。 基坑开挖引起建(构)筑物沉降的预测方法主要有经验法、数值模拟法和智能预测法等[2]。 其中,经验法通过建立建(构)筑物响应与影响因素间的经验关系来预测施工过程中建(构)筑物的施工响应,该类方法考虑的影响因素不够全面,尤其是无法考虑基坑周边环境的复杂性。 数值模拟方法多通过与现场监测数据结合,来研究既有建(构)筑物与施工的相互影响[3]或者是工前评估[4]。 数值模拟方法在建模过程中需要对场地条件进行一定的简化,因此,与现场监测结果有一定差距,并且计算工作量太大,很难直接应用于基坑工程中的建(构)筑物的施工响应预测。 随着近年来人工智能的快速发展,智能预测方法逐渐被引入到基坑开挖的变形预测中。 例如,Fuxue Sun[5]应用SVM(支持向量机)对某一软土地区深基坑变形进行预测,证明SVM 在变形预测的模糊岩土工程问题上具有良好的性能;王俊峰等[6]利用粒子群算法对SVM 模型的参数寻优,进一步提高其在深基坑变形的预测精度;葛长峰等[7]应用BP 神经网络和RBF 神经网络论证人工神经网络用于预测基坑周边地表沉降的可行性和准确性;宋楚平[8]通过遗传算法对BP 神经网络深基坑模型权重初值进行优选,减小预测误差,同时提高模型的收敛速度。
上述分析表明,传统预测方法难以考虑施工过程中影响因素的复杂性和不确定性,有一定的局限性。 基于机器学习的智能预测方法是未来研究的发展方向,但现有建筑物沉降单一因素的预测研究具有较为明显的局限性,需进一步考虑多因素影响既有建(构)筑物沉降的间接预测。 基于上述考虑,本文基于机器学习中的SVM、BP、SVM-BP 组合算法的预测模型,结合实际工程,考虑基坑监测过程中7 个常规监测项目影响因素,对实际工程基坑开挖引起邻近建筑物的变形进行模型应用分析。
1 基坑开挖诱发周边既有建筑物沉降的间接预测方法
1.1 既有建筑物沉降间接预测体系构建
深基坑开挖往往伴随基坑底部隆起、围护结构变形、周围地层移动,进而诱发周围既有建(构)筑物产生影响其安全的变形。 本文聚焦于基坑周边既有建筑物的沉降,基于常规基坑监测项目,构建一套基坑开挖诱发周边既有建筑物沉降的间接预测方法。
《建筑基坑工程监测技术规范》(GB50497—2009)针对各种基坑类别建议了不同的基坑工程监测项目。 其中,一级基坑应测监测项目包括围护墙(边坡)顶部水平位移、围护墙(边坡)顶部竖向位移、深层水平位移、立柱竖向位移、支撑内力、锚杆内力、地下水位、周边地表竖向位移、周边建筑的响应(包括水平位移、竖向位移、倾斜和裂缝)等。 基坑工程是一个系统工程,在基坑开挖过程中,上述监测项目的响应紧密联系,既有建(构)筑物沉降可以用其他几个变形相关的监测项目表达。因此,本文拟构建如图2 所示的周边既有建筑物沉降预测体系,选择一级基坑应测的7 项监测项目作为输入影响因子。 其中,基坑内的影响因子包括围护结构深层水平位移和桩顶水平位移、与围护结构沉降变形相关的桩顶竖向位移、反映基坑底部隆起和支护结构内力的立柱沉降和支撑轴力;基坑外的影响因子包括基坑周边地表沉降,以及基坑周边地下水情况。 本文基于机器学习的方法确立输入影响因子与周边既有建筑物沉降之间关系,该方法是基于海量数据寻找影响因子与周边既有建筑物沉降之间的关系,其属于自主学习,不需要建立明确的关系式。 机器学习方法使用中的一个关键难点是定性变量的处理,常见的处理方法有两种:(1)将定性变量转换为多个虚拟变量;(2)将定性变量转换为定量变量。

图2 周边既有建筑物沉降的预测体系Fig.2 Prediction system of the settlement of existing buildings around the foundation pit
根据工程案例的特点,本文在构建影响因子与周边既有建筑物沉降关系的过程中选择将定性变量转换为定量变量。 即基坑周边地表沉降依据文献[9]进行权重划分后再结合实测值进行计算;深层水平位移取当日各监测点变化的最大累计值;桩顶水平位移和桩顶竖向位移均取当日各监测点变化的最大值;基坑周边地下水位取平均变化值;支撑轴力先按设计值进行权重划分,再结合实测变化值进行计算。
1.2 基于机器学习的模型实现
1.2.1 支持向量机
支持向量机(SVM) 是一种以统计学理论为主导的机器学习算法,最初针对线性分类问题提出,后来由Vapnik 等在SVM 分类的基础上引入不敏感损失函数ε,从而得到用于回归型的支持向量机,并取得比较好的性能和效果[10]。 SVM以最小经验风险为约束条件,对经验风险的固定,通过置信范围最小化来最小化结构风险[11],可以很好地解决样本不足的问题。 SVM 用于回归分析时,其基本思想是寻找一个最优分类面,使所有训练样本距离该最优分类面的误差为最小,如图3 所示,通过一个非线性映射F 将数据xi映射到高维特征空间M 中,并在这个高维空间中构造出最优线性回归函数。 具体做法是通过一个核函数映射将非线性映射到高维空间,不同的核函数可以构造出不同的支持向量机。

图3 SVM 基本思想Fig.3 SVM basic thought
基坑开挖过程中周边建筑沉降与基坑变形影响因子间存在着显著的非线性关联。 因此,需要借助于核函数,通过非线性变换实现非线性问题向对应维度线性问题的转变,进而达到分类超平面的最优化。 采用SVM 求解回归问题的关键是核函数和参数的选择。 径向基核函数(RBF)具有很高的灵活性,对应无穷维特征空间,有限样本在该特征空间中线性可分[12]。 本文选径向基核函数(RBF),其表达形式为:
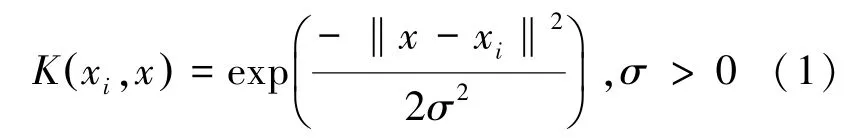
式中,σ 为均方差,可以通过调控σ 值来调整核函数。
选择RBF 为支持向量机的训练核函数时,SVM 算法的复杂度、精度和泛化能力等特性受不敏感参数ε、惩罚系数c 和宽度系数g 的取值以及相互关系的影响[13]。 其中,ε 直接体现模型中数据不敏感范围的宽度,以函数的最小化为特征,确保对偶变量的稀疏性、全局最小解的存在和可靠泛化界的优化。 c 表示模型对超出ε 间隔数据的惩罚力度,影响模型的稳定性。 c 越高,越不能容忍出现误差,容易过拟合;c 越小,容易欠拟合;c 过大或过小,泛化能力都会变差。 g 是RBF 函数自带的一个参数,表示各支持向量之间的关联度,影响数据映射至高维空间里的复杂度。
本文利用台湾大学林智仁等开发LIBSVM3.23 工具箱进行参数分析,寻求最适合本文研究的核函数模型。 模型的输入特征项包括周围地表沉降、深层水平位移、周边地下水位、支撑轴力、桩顶水平位移、桩顶竖向位移和立柱沉降。 为避免输入向量中变量数量级相差过大而影响训练效果,调用scale 模块对训练数据和测试数据进行归一化处理,归一化区间为[-1,1]。SVM 的建模流程如图4 所示。

图4 SVM 的建模流程图Fig.4 Flow chart of SVM modeling
1.2.2 BP 神经网络
反向传播(BP)神经网络由输入层、隐含层和输出层构成,层与层之间多采用全互连接方式,同一层神经元之间相互独立,其拓扑的结构如图5所示。 BP 神经网络具有简单易行,准确度高等特点。 BP 神经网络以误差反传误差为依托实现学习方法的反向传播,通过对训练样本的持续学习,不断调整层次间的阈值和连接权值,最终实现由输入层节点向输出节点的转移。 单层节点的输出只同下一节点输出存在密切关联.如果输出层的输出达不到预期水平将导致误差信号反向传播流程的逆向发展[14]。 误差反向传播得到各个神经元的参数后,信息前向传播根据各个神经元的参数,得到神经网络的输出。 两个传播过程交替进行,在有权向量空间上使得误差函数的梯度下降,动态迭代确定某组权向量,获得最小化的网络误差函数,完成信息提取和储存工作。

图5 BP 神经网络拓扑的结构示意图Fig.5 Structure diagram of BP neural network topology
本文采用3 层神经网络开展研究,利用Matlab 软件中的神经网络工具箱提供的newff 函数、train 函数、sim 函数实现网络构建、训练和预测。 训练过程中,采用的输入影响因子共有7 个,故输入层节点数(m)为7;期望输出结果只包含既有建筑物的沉降1 个指标,期望输出维数为1,故输出层节点数(n)为1;隐含层神经元个数为:

式中,k 为神经元个数;m 为输入层节点个数;n为输 出 层 节 点 个 数; α 为 常 数, 取 值 范 围为1~10。
对原始数据、训练样本、测试样本等作归一化处理后,选取7 个监测项目的监测数据作为已知输入,周边建筑物沉降值作为输出标签,迭代训练,构建网络。 用周边建筑物真实沉降数据作为教师信号,当计算输出值与教师信号之间的误差小于设定允许值时,训练结束,得出网络的收敛曲线,保存训练好的BP 神经网络结构和参数。 将需要预测的样本输入训练好的网络,即可得出既有建筑沉降值,并反归一化结果。 BP 神经网络的建模流程如图6 所示。
1.2.3 SVM-BP 组合算法
为充分利用不同机器学习算法的优势,减少信息丢失,降低不确定性,提高预测精度,可以将不同的机器学习算法进行有机结合。 考虑SVM和BP 神经网络方法在问题研究中的适用性,本文采用公式(3)将SVM 算法和BP 神经网络有机结合,构建SVM-BP 组合算法。式中,x 为组合预测值,xi为第i 种算法获得的预测值,ki是第i 种算法所占权重,本文取n =2。

图6 BP 神经网络的建模流程图Fig.6 Flow chart of BP neural network modeling
为确定最优的ki,依据最优准则(如最小二乘准则、极小极大化准则等) 构造目标函数M,在权重之和为1 的约束条件下使M 的值极小化,求得组合模型的加权系数。 权重的选取主要考虑单个模型的相对误差,误差小的权重大,误差大的权重小。





图7 SVM-BP 组合模型建模流程图Fig.7 Flow of SVM-BP combination model modeling
2 工程实例
2.1 工程概况
中心医院站是徐州市轨道交通2 号线一期工程的中间站,位于解放南路西侧,徐州市中心医院对面,沿解放南路铺设。 车站采用明挖顺筑法施工,车站起点里程为右DK10+194.386,终点里程为右DK10+431.587,车站主体基坑长238.20m,宽21.7m,深16.59m,采用分层分段开挖。 本文选取1 至9 断面的监测点对周边商铺楼的阳角点JGY-22(图8 中红色标出)的沉降作为研究对象。为验证本文方法的合理性,收集徐州市中心医院地铁站第70 期到180 期监测数据,其中选取前103 期中的80 期为学习样本,剩下的23 期为测试集用来检验学习情况,之后的7 期作为预测集进行现实预测。
2.2 预测模型验证
为更好地描述前述SVM、BP 神经网络和SVM-BP 组合3 种算法在建筑物沉降预测中的精度和适用性,选用均方误差和决定系数两个指标对模型的精度进行比较分析。
均方误差(MSE)是反映估计量与被估计量之间差异程度的一种度量,其表达式为:

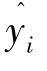
决定系数(R2)表示自变量对因变量的解释程度,在0~1 取值。 取值越大表明自变量引起的变动占总变动的百分比越高。 决定系数越高,拟合效果越好,解释变量对预报变量的贡献率越高,解释变量和预报变量的线性相关关系越强。 其表达式为
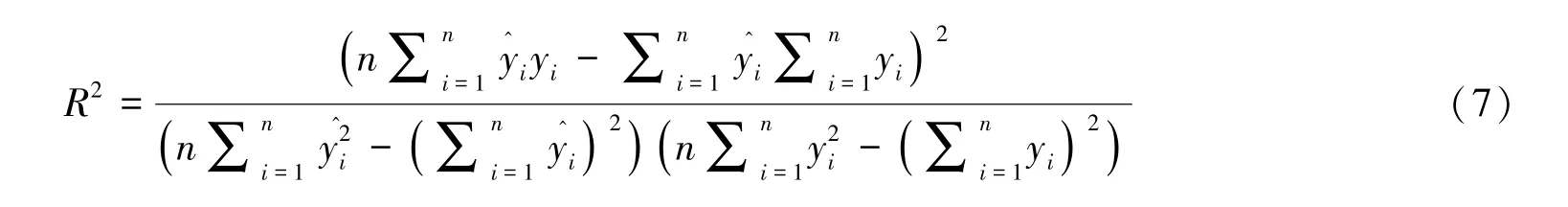

图8 监测布点图(部分)Fig.8 Layout of part monitoring points

2.2.1 基于SVM 的预测模型
由前所述,本文依托MATLAB 软件平台,利用libsvm 3.23 工具箱进行SVM 参数分析。 调用SVM 为ε-SVR 类别,基于交叉验证和网格搜索对SVM 进行参数寻优,采用最佳参数c 与g 对整个训练集进行训练获取支持向量机模型的最优参数,见表1。 图9 给出测试集样本数据与基于SVM 的预测模型得到的测试结果的对比。 由图9可知,除个别数据点外,基于SVM 的预测模型较好地预测基坑周边既有建筑物沉降量,均方误差值为0.1159,预测模型得到的建筑物沉降的跳跃性小于实测结果的变化。

表1 SVM 模型参数值Tab.1 Parameter values of the SVM model

图9 SVM 预测值与测试集真实值对比图Fig.9 Comparison between SVM predicted value and true value of the test
2.2.2 基于BP 神经网络的预测模型
针对本工程实例,BP 神经网络采用单隐含层设置,输入层节点数(m)为7;最优隐含层神经元个数L 通过比较MSE 值的大小选出,最终确定隐含层的节点数目为10。 由基于BP 神经网络的预测模型得到的测试结果与测试集真实值对比如图10 所示。 由图10 可知,采用基于BP 神经网络的预测模型得到的周边既有建筑物沉降量,除开始8 天的预测值略大于真实值之外,其他时间段的结果与监测结果基本吻合,与真实建筑物沉降趋势一致,均方误差仅为0.121。

图10 BP 神经网络预测值与测试集真实值对比图Fig.10 Comparison between BP neural network predicted value and true value of the test
2.2.3 基于SVM-BP 组合算法的预测模型
由前结果分析可知,基于SVM 支持向量机预测模型和基于BP 神经网络的预测模型所得的结果和实测值整体相符程度较高,预测结果较好地反映基坑开挖作用下既有建筑物沉降的变化趋势,可以较好地指导建筑物的沉降预警工作。
为检验基于SVM-BP 组合算法的预测模型的适用性,根据前述基于SVM 的预测模型和基于BP 神经网络的预测模型两种方法得到的测试结果,按照1.2.3 所述方法,求取两种预测模型的最优加权组合权重,见表2。 图11 为利用SVM-BP组合预测方法得到的测试结果与测试集真实值对比。 二者吻合度非常高,均方误差小于0.1,能够很好地反映监测值的变化。

表2 组合模型预测权重Tab.2 Forecast weight of the combination model
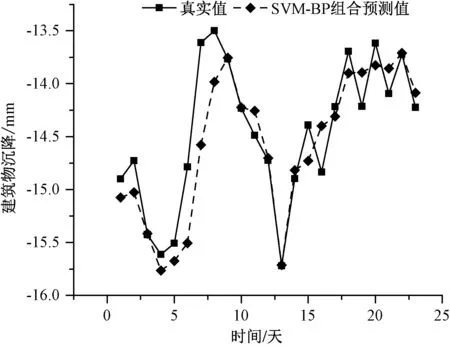
图11 组合模型预测值与测试集真实值对比图Fig.11 Comparison between combination model predicted value and true value of the test
图12 给出3 种预测模型与真实值的绝对误差,由图可知,3 种模型的预测结果与真实值的绝对误差均小于1mm,满足工程需要,但SVM-BP组合算法的预测模型误差曲线总体更平滑,更接近零线。
表3 列出3 个预测模型的相对误差均值和决定系数。 由表3 可知,本文3 个预测模型的决定系数均大于0.6,满足预测的精度要求,均可以用来进行后续建筑物沉降预测。 其中,基于SVMBP 组合算法的预测模型所得结果的均方误差最小、决定系数最高,说明该预测模型具有最好的精确度、拟合效果最好。

图12 3 种预测模型绝对误差对比图Fig.12 Comparison of absolute errors of three prediction models
2.3 基坑开挖诱发既有建筑物沉降预测
基于上文已经训练好的3 种预测模型,利用预测集样本进行预测检验。 表4 列出3 种模型的预测结果以及其均方误差(MSE)和决定系数(R2)。

表3 测试集均方误差和决定系数Tab.3 Mean square error and determination coefficient of the test

表4 预测集拟合结果Tab.4 Prediction fitting results
由表4 可以看出,3 种预测方法的决定系数均大于0.6,均较好地反映上述影响因子与建筑物沉降的关系。 相比而言,基于BP 神经网络的预测模型决定系数较小,说明该预测模型描述解释变量(影响因子)对预报变量(建筑物沉降)的贡献率偏低;而基于SVM 的预测模型相对较好,决定系数高,贡献率大。 利用基于SVM-BP 组合算法预测模型得到的建筑物沉降最接近于真实值,误差最小,决定系数大于0.8,表明该预测方法很好地描述影响因子对建筑物沉降的贡献率。 基于SVM-BP组合算法的预测模型可以有效地提取单一方法的优点,提高数据的利用率,增强预测模型的可靠性,使得预测结果的准确性进一步提高。
3 结论
本文以基坑开挖作用下周边建筑物的沉降为研究对象,建立基坑周边既有建筑物沉降预测体系。 从机器学习应用出发,分别利用SVM 和BP神经网络建立建筑物沉降预测模型,进而,结合两种算法的优点,建立基于最小二乘法的最优权重SVM-BP 组合预测模型。 利用某基坑工程,实测数据对所建立的建筑物沉降预测模型的适用性进行验证。
(1)基于基坑周边地表沉降、深层水平位移、基坑周边地下水位、支撑轴力、桩顶水平位移、桩顶竖向位移和立柱沉降7 个常规监测项目构建基坑开挖周边建筑物沉降的预测体系。 依据工程项目特点和力学机理,对监测数据进行适当处理,与机器学习充分结合。
(2)本文应用的3 种预测模型均能很好地预测基坑开挖诱发的既有建筑物沉降,最优加权组合预测模型具有信息利用最大化和均方误差最小的特点,与单一模型比较,预测精度较高。 对实际工程基坑开挖引起邻近建筑的变形进行模型应用分析,研究内容对其他工程具有一定的借鉴意义。

