经济生活中经济数学的应用分析

周安宁

（平凉技师学院，甘肃 平凉 744000）

在现代高校教学中，经济数学强调现实运用，但大多金融类高校对缺乏内容深入，多是讲解经济数学的相关定理和概念，让学生缺乏了数学学习兴趣。

值得注意的是，金融类高校数学教育在强调改革的同时，虽然改革了大量的内容，但是在实际应用方面存在很大的问题，一方面，学生对数学的兴趣不断下滑，数学教学缺乏生活化的案例，导致学生长期在数学概念和理念的教学，没有真实激发学生的学习兴趣。另一方面，学生对数学教学意义认识不到位，认为经济数学是研究宏观经济的“高大上”学科，其不愿意从生活中反思数学知识，且极少运用数学知识来解决生活问题或者是经济问题。对此，如何打破传统的经济数学教学模式，将经济数学教学深入到经济生活中成为了现代教育管理的重点内容。

本文针对经济数学在经济教学中的价值和意义进行了研究，以案例分析的方式，阐述了经济数学和经济生活中的关联性，结合数学案例发挥了经济数学在经济生活中的引导性、决策性作用，希望能够为高校优化教学，培养更多数学人才提供参考借鉴。

一、经济数学在金融经济中的运用价值

（一）经济生活和经济数学思维的融合

经济数学对比其他的信息、工程、文学类学科更强调逻辑性和理论性。将经济数学和学生的生活联系在一起，可以帮助学生理解和解释生活中生活想象，通过经济数学思维引导，数学案例分析，提升学生的知识运用能力，最终学生从多个角度来验证数学猜想、帮助商业、金融机构作出正确的决策。

对于数学学科的发展而言，经济生活也成为了经济数学的佐证，经济生活的结果也为验证经济数学的定义和规范原理提供了重要的实践论证依据。基于经济发展建设环境，借助经济数学的教学，可以让数学有机融入经济学环境中，也能强调经济学理论实践化运用，在推动经济产业健康发展的同时，帮助更多的企业、机构、个人了解经济生活中的供求关系，进一步促进金融经济和数学建设有机融合发展。

（二）可以预测经济发展趋势

经济生活和经济数学思维的融合可以有效预测经济发展方向，企业管理人员开可以根据经济预测制定对应的对策计划。经济数学具备数学学科演技结构性和逻辑型的特征，通过模仿经济生活的运作原理和数学规则，制定经济数学分析模型和数据算法，可以及时预测经济发展的方向，以保证经济发展有迹可寻。

现阶段经济发展中，大量的经济学理论都融合了数学知识，在具有科学依据的数据演算和推理下，经济数学为预测经济发展趋势做出了重要的铺垫作用，也为中国经济的好又快地建设发展指明了方向。

（三）解释经济现象

经济数学思维在经济学中有广泛运用，通过经济理论研究和实战中，人们对经济学的理论有了更加科学的认识，这也让高深莫测的经济现象变的规律化、客观化。利用经济数学，有效分析了经济体系的建设意义和方向，对于推动经济建设发展也有客观作用，这体现了经济数学解释经济现象的价值。此外，在更深层次的角度分析，掌握了经济生活和经济数学的内涵，也能够让经济数学发展更有针对性和可控性，可以让金融数学的内容和内涵变得更加科学化，及时避免了经济活动中的错误倾向，可以减少经济管理中的弊端和缺陷，扭转经济困局。

二、数学经济现阶段运用存在的问题

（一）数据来源不确定

高校数学经济教学中多存在着教学资源来源不真实等问题。

一方面，数据来源不确定的，导致所用数据在经济发展中缺乏科学考证运用不符合现实逻辑。例如随着经济建设，物价上涨，以往的物价指标和如今的物价指标有天壤之别，又或者商品物类的差异性也会导致数据运用的差异性。另一方面，数据来源是否真实也关乎到了经济数学的预测效果，若数据属于杜撰，其不能体现现实生活中的经济关系，也会导致数据模型缺乏真实性，不满足经济数学的运用要求。

可见，在经济数学的研究和分析中，一定要保证数据的真实性，不建议选用模糊或者是落后的数据，预防对数据分析、数据演算造成负面影响。数学学科强调逻辑性和严谨性，若出现严重的数据误差，其研究结果的实用性也无法为现阶段经济分析和发展预测提供帮助。可见，对应的研究人员应当保证数据来源真实可靠，以体现经济数学的应用价值。

（二）经济现象分析考虑不全面

随着我国经济建设不断发展，人们对经济现象的关注积极性越来越高。在现实的经济建设中，经济数学教学的分析方式、环境也受到了多种环境影响。例如数学方程式分析，若单从按基本的变量分析经济现象，可能不符合多变量的社会经济影响原则；若选用变量过少，也无法保证其预测结果科学真实。对此，为保证经济数学预测真实性和有效性，研究人员应当做好实地考察，收集相关的影响数据，形成科学、完善的经济报告，保证数学分析结果真实可信。

三、经济生活中的数学运用案例

（一）线性代数的投入产生模型

1.投入产出模型。本次研究分析的是投入产出模型，分析了经济主体之间的各个部门之间的联系性。其中投入产出模型研究的内容是经济体的产出和投入之间的关系。可以通过建立分析表和平衡方式来研究。其中横向平衡消耗方程可以为：

产出投入中的竖向消耗方程为：

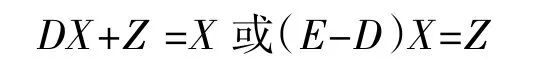
其中A 为直接消耗矩阵、Y 为最终消耗量、D为系数、X 为总产出、Z 为最终投入量。

2.多变量数据时间模型。多变量数据时间分析模型试分析方式是分析经济未来发展方向，其常用的分析法有VAR（自回归模型），MA 模型（移动平均模型）等，本次研究自回归模型为研究方式，采用联合方程计算变量的滞后值，计算回归结果，进而估算生成的变量动态关系，常用的分析对象可为汇率、物价等、以物价未分析趋势，形成两个自回归计算模型：

经过联合计算分析研究后，可以形成以下关系：

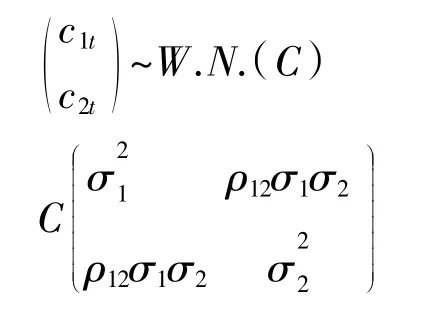
其中ρij=Corr（cit，cjt），（1臆i臆2，1臆j臆2），σ 为标准方差，Cit～IID（0，σ2），（1≤i≤2）。

矩阵计算转化后如下：

（二）微积分的边际应用分析

1.边际效益分析

经济学分析中，边际分析问题十分常见，其多存在于成本变化、利率变化等问题中，为了帮助企业找出合适的边际效益变化规律，可以借助经济数学分析来研究计算。

先选取某汽车生产厂家研究分析，一台汽车售价为30 万元，成本函数C 可如下表述：

利润函数如下：

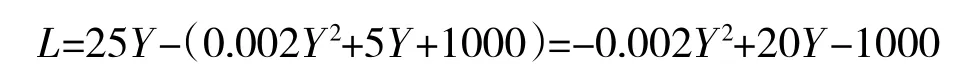
可以利用微积分的边际效益来计算利润的增长率以及最大利润。如下所述：经过边际利润计算分析，可以获得以下生产台数和利润变化的关系：

表1

2.弹性分析

价格弹性也是经济数学分析的最常见内容，例如同类商品上涨一元钱，对比原有价格而言，其涨幅关系存在区别，且供需关系也存在变化，弹性分析实际上是分析需求对商品价格的影响，当价格变化时候，商品的需求就发生波动。相对变化率即如下计算方式：

3.概率论分析运用

（1）预测精准度。概率论可以预测数学经济的分析精准结果，一般而言，预测有且仅有对和错两种结果，每种结果的P=1/2，相对某22 次“回预测”研究分析，以K 为概率预测错误的回数，可以得到以下累加计算结果。预测计算方式为：

累计计算结果如表2 所示。

表2

以上可知，选用22 个抽样样本中，6 次以下的抽样结果具有针对性，表示预测结果有效。

（2）回报率和风险评估。现分析某企业的三种投资方式。A 方法的非常盈利值为100，一般盈利值为15，亏损值为-30；B 方法的非常盈利值为70，一般盈利值为25，亏损值为-10；C 方法的非常盈利值为80，一般盈利值为20，亏损值为-20；按照非常盈利、一般盈利、亏损可能性分析，可以分为非常盈利（P1=0.3）、一般盈利（P2=0.6）、亏损（P3=0.1）；经过盈利计算分析：

三种计算分析下，A 收益最大，考虑风险因素下，可以计算个方案的方差：

以上可知，虽然A 收益最大，但是其方差值大，存在即较为明显的收益波动值，虽然B 的收益不如A 理想，但是其风险低于A，且最低，综合考虑，B 方法投资最安全，收益合理。

四、对数学经济分析的改进措施建议

经济的产生不是自然现象，是人类社会文明发展的必要产物。货币的产生，一方面是基于社会认同的前提下诞生的，另一方们也是为了方便人类经济交换活动。可见，经济和货币都是人为产物，这一点和数学起源相同。可见，经济诞生初期就和数学紧密相连，数学为经济生产和经济效益提供量化作用，经济和数学的实质性关系就是数量变化和供求关系的表达。

从生活经济表现来看，数学帮助生产单位实现了面包分配，土地测量和物品堆积体积等问题，随着现代经济的研究发展，数学所变调的规律性和价值作用远远高于经济。因此数学也成为了一门独立的学科。

从企业经营建设角度分析，当代经济主体有个人、企业、政府等，经济内容也涉及到了金融经济、财政经济和财务管理几个方面。经济运动的主体有借贷双方，且二者关系处于动态平衡，这要求资产负债的合计相等，且有经济收益增加就一定有经济收益损失。此外，时间也会制约经济作用，一个特殊的时间点无法实现经济平衡收支，仅在一个理想的时间段中才能够实现经济作用，这也是企业长期资金运作和短期资金运动常见的差额经济。如何实现短期利益的最大化，保护经济市场规律运行，需要以经济数学分析为依据，做出对应的数学分析和研究，实现经济利益分配的最大化。对此，笔者提出了以下几点措施建议，希望能够为高校教育，企业管理提供生活经济数学分析措施建议。

（一）确定数据来源

确定数据来源的真实性可以保证数学模型、演算方法正确。若在经济建设发展中，能够在原有经济分析基础上分析现有经济发展的趋势，可以保证数据来源的可靠性。进而让数学分析对经济活动预测更加精准。对此，研究人员应当理性分析数据来源和数据的科学性。例如在分析某一项经济活动时候可以率先考察，保证数据源头的数据可靠性，最终确定经济建设的方向，确保经济建设在可控范围内。

（二）分析经济体系

以上案例可知，经济分析不光要看收益，更要分析风险，评价一个经济活动的运动趋势，要考虑多变量，且不可以分析单一变量。为了保证生活经济分析的原因和结果真实可行，需要研究人员理性分析数据的来源和影响因素，例如在关注经济利润和收益时候，考虑生产和销售时候，也要考虑通货膨胀等带来的影响。建议研究人员分析经济现象时候，多考虑非数据因素的影响，例如不可抗力、社会科技进步、群众消费特点等。以此才能够将多种因素如商品的成品、发展趋势、可替代产品等对产品的影响整合在一起，构建科学的数据模型，进而进行数据演算和分析，制定出适合企业科学发展，宏观建设的措施。

（三）改善数学演算方式

经济生活的概念和内容也随着人们的生活水平提升大有变化。现阶段，生活经济处于一个变动的环境中，经济的结果也受到了多方面因素的影响。数学分析方式虽然适用于现代社会的一些经济现象，但依旧不能够完全判定经济发展方向，其仅能作为预测依据，没有肯定判断的作用。对此，经济数学研究单位应当针对经济活动的运动方向以及规律展开研究，深入挖掘经济数学的使用效率和价值，并为创新经济建设，优化经济实用建设而做出贡献。

五、对高校优化经济数学教育的措施建议

（一）以激发学生内在学习动力为主

随着我国教育事业的蓬勃发展，数学教育为我国经济建设做出了重要的贡献。但数学教学难度大，数学知识有概念多、逻辑性强的特点。大多学生存在厌学的情绪。

要想用数学知识创造价值，需要付出大量艰辛汗水才可能有收获。我国传统的经济数学教学强调的是学生的艰苦学习精神和毅力，没有考虑到学生的实用价值，导致学生对经济数学知识存在一种理论知识学习的偏见。美国数学家罗杰斯认为，数学教学应当从学习目的和学习兴趣入手，让学生感受到逻辑推理的乐趣，以此来淡化枯燥学习的情绪、可见，大多学生在理论化教学中失去了自信心。只有提升学生对知识的内驱力才能够培养出更多的数学人才。以上可知，高校数学教学对经济数学这一学科认识不明，大多学生没有在学习中体会到学习价值，其根本原因是缺乏学习兴趣、自我创造的欲望和乐趣。

对此，建议高校教师在讲解数学经济原理时候，多为学生讲解社会上的经济现象，历史人物故事，数学和经济之间的发展关系，将数学知识和生活趣味相结合，以此来提升学生对数学知识的兴趣。教师也应当积极鼓励学生探索数学知识，多为其讲解数学公式定理发现故事，让学生也善于思考，提升自己对经济数学的好奇心。

（二）注重实用性教学，弱化概念讲解

当代数学教学中，很多经济数学教学重视理论，淡化实践应用，学生对数学学习的积极性不高。一方面，院校是启迪学生思维，给予其知识养分的环境，学生处于学习阶段，院校不会直接将学生推向社会实践，更多的是理性指导。另一方面，数学知识具有逻辑性和严谨性的要求，为了保证教学知识，学生必须要理解经济现象和数学原理。理论化的知识教学是学生获取知识的必要前提。大多教师在学生已有的理解基础上重复教学，这导致了理论教学过重，学生的学习积极性不高，教学质量不高。

建议教师做好知识教学引导，从生活中选取一些案例，帮助学生形成积极的思考习惯。例如书本中的变化率问题，专业教师会为学生讲解成总产量的变化量，总成本对产量的导数就是产品的边际成本。若单一讲解数学概念知识，学生也大多会昏昏欲睡。对此，建议教师在课堂前多为学生讲解和本学科相关的知识，以此为学生构建正确的数学概念和观念，最终拓宽学生的思路，让学生将理论知识不断转化为解决数学知识的能力。

（三）从职业化教育途径入手

以职业化教学为方向培养人才，决定了他们不必对数学公式、定理的来龙去脉像学术专家生那样对所有的数学定理要搞得清清楚楚，而是要能用这些公式来解决实际运算问题。因此，在课堂教学中，不必要的、耗时较多的理论推导、公式证明都可删减。例如函数极限的性质只是作以介绍函数求导的四则运算法则，只推导函数乘积的求导公式，对和、差、商的求导法则就不再一一推导函数极值的必要条件、函数极值的判断方法，也不去做严格的数学证明，只要给出几何图形，作直观的几何说明，学生能够接受就可以了。数学是他们从事专业工作的工具，学数学主要是为了用来解决工作中出现的具体问题，这种人才规格决定了使用数学工具的重要性。在教学中我们必须改变过去忽视各种数表、计算器等工具的应用，改变数学考试时不允许将计算器带进考场的规定。因为我们培养的人才在今后的工作中如果遇到了数学问题，是通过数表、计算器、电脑等工具能迅速、准确地得到结果，达到完成任务的目的。提高高职数学教学的质量，就是要在学生已掌握必备的高中数学知识以后，为他们进一步提供今后工作岗位所必需、够用的数学基础知识，为他们学好专业铺平道路、打下基础。要获得好的教学效果，需要走很长的路，只有一步一个脚印地走下去，才能接近最终目标。

六、结语

综上所述，本文针对经济数学中常见的经济数学案例进行了分析，对常见的生产投入产出、经济收益预测以及优选投资方案进行了研究分析。案例虽然简单，但也揭示了经济现象。对此，希望借助该方式帮助学生积极认识数学在经济管理活动中的价值和意义，帮助学生明确经济数学的实用性，希望对应的院校结合生活经济案例，采用项目驱动教学和教学引导法，让更多的学生理解和认识世纪经济学系中存在的数学问题，并积极开发学生的数学思维，引导学生用所学的数学知识，不断解决生活中常见的经济问题，最终为优化经济教学，首先数学知识活学活用的目标，也更进一步地为社会经济建设发展做出贡献。