基于不同度量的指纹定位算法比较
韩雨辰 仲臣 徐锦修 刘清华


摘 要:在指纹定位加权K近邻算法中,传统欧氏距离度量原理简单,但会忽略掉样本单元不同特性之间存在的差别,导致定位误差较大。为了克服欧氏距离存在的不足,分别采用马氏距离、卡方距离将其替换,并结合加权K近邻算法进行定位精度对比。试验结果表明,取相同K值的情况下,基于马氏距离度量对指纹定位精度的提升较低,基于卡方距离度量的指纹定位精度明显优于另外两种方法。
关键词:K最近邻;欧氏距离;马氏距离;卡方距离
中图分类号:TP391.4;P228.4 文献标识码:A 文章编号:2096-4706(2020)21-0020-04
Comparison of Fingerprint Location Algorithm Based on Different Measurements
HAN Yuchen,ZHONG Chen,XU Jinxiu,LIU Qinghua
(School of Space Information and Surveying Engineering,Anhui University of Science and Technology,Huainan 232001,China)
Abstract:In the fingerprint location weighted K-nearest neighbor algorithm,the traditional Euclidean distance measurement principle is simple,but it will ignore the difference between different characteristics of the sample unit,making the location error larger. In order to overcome the shortcomings of the Euclidean distance,Mahalanobis distance and Chi-square distance are used to replace them,and the weighted K-nearest neighbor algorithm is combined to compare the positioning accuracy. The test results show that,under the condition of taking the same K value,the accuracy of fingerprint location based on Mahalanobis distance measurement is less improved,and the accuracy of fingerprint location based on Chi-square distance measurement is obviously better than the other two distances.
Keywords:K-nearest neighbor;Euclidean distance;Mahalanobis distance;Chi-square distance
0 引 言
随着科技的不断进步,以GPS为主的室外定位技术已趋于成熟。如今,随着最后一颗北斗三号卫星成功发射,我国北斗卫星导航系统就此迈入世界前列,其定位精度最高可达到1至2米,足以满足人们的日常出行需求。同时随着现代化城市的发展,一些单体建筑的建造规模也越来越大,室内面积迅速增加,研究表明,人们每天的具体活动区域接近80%均在室内,因此,室内定位逐渐成为研究热点。室内定位技术整体由广域室内定位技术和局域室内定位技术组成[1]。广域室内定位技术主要通过大面积的数据通信网络来实现,早在2002年,欧盟在伽利略计划中率先提出伪卫星技术,即通过构建卫星发射装置,生成卫星信号从而模拟导航卫星的工作状态,在一定区域内提高其定位功能;由于房屋墙体等遮挡,GNSS信号在传递到室内时其信号强度几乎不可能用来直接进行定位,可利用移动通信网络对其进行“帮助”,增强传送的改正数据,为移动接收机提供附加信息,使GNSS信号达到满足定位需要的信号强度,即辅助GNSS技术;同样基于通信网络系统进行室内定位的还有导航通信一体化定位技术[2]。局域室内定位是以室内物理支撑设施为基础,通过某种信号介质完成定位的技术。其技术包含Wi-Fi技术、紫蜂技术、蓝牙技术、射频识别技术、超宽带技术、惯性单元技术、超声波定位技术、红外线定位技术、地磁定位技术、可见光定位技术等[3]。用户通过终端设备接收物理基础设施所发出的信号,结合多源数据并通过一系列算法解算,以此获取最终的位置信息。室内定位的应用很广泛,在某些企业的大型车间,往往需要对贵重的产品运输或者工作人员流动进行轨迹定位,以方便更好的管理与规划;在幼儿园或养老院等特殊场所,可对老人或孩子的行程轨迹进行针对性的跟踪定位,以防发生迷路或走失等意外情况;消防救援方面,可在消防队员身上安置定位设备,确定他们的位置以及安全状况,同时方便消防队员更准确的了解事故场地的内部构造,规划逃生路线,提升救援效率。基于“人工智能时代下导航工程专业人才培养模式研究”项目,笔者长期致力于新型室内定位算法的研究,并在研究过程中将机器学习和室内定位方向进行结合,对机器学习加权K近邻(Weighted K-Nearest Neighbor)算法中的不同距离度量进行多次算法实验,对进一步提高室内定位的精度有一定的参考意义。
1 研究现状
从某些角度来看,室内定位的研究面临着更复杂的难题。首先室内的面积相对较小,这意味着室内定位的精度要求更高。其次室内情况一般较为复杂,人员的频繁流动、设备的变迁都会对定位精度造成影响,同时室内通常会摆放一些含有金属材质的物品,会对信号的传递产生较大干扰,导致因信号稳定性较差而无法进行室内定位的情况出现等。因此,如何使室内定位达到更高精度成为国内外众多学者的研究方向。文献[4]是由Youssef提出基于位置指纹库的室内定位系统,即将所采集的位置点信息与其对应的信号接收强度相结合来建立位置指纹库,利用相似度匹配从指纹库中获得相应的位置信息。在文献[5]中,王培良通过分析紫蜂无线网络系统,对均值阈值和频率阈值进行滤波处理,在离线阶段建立了更高精度的指纹库,并将WKNN算法及模糊C均值聚类算法应用到在线定位阶段。在文献[6]中,倪巍等人基于RSSI中存在的误差随机变量,通过有限次迭代对最大似然估计算法进行改进,从而修正距离损耗模型。文献[7]是由孙瑜分析LARNDMARC室内定位系统的原理,将射频识别与最近邻改进算法相结合,提出了一种改进的数据融合定位方法,并将误差多级处理引入室内定位。在文献[8]中,研究人員将紫蜂信号应用到Wi-Fi指纹定位中,并利用曼哈顿距离代替欧氏距离对K近邻算法进行改进,提出了Wi-Fi/紫蜂融合定位技术,实验表明该技术相较于传统Wi-Fi指纹定位获得了更高的定位效果。
2 室内定位方法
室内定位的方法有很多,如今作为主流方法的是三角测量法、临近法、行人航迹推算法、指纹定位法[9]。三角测量法的基本原理是首先测出待测点到至少三个已知设备点之间的距离,可由电磁波信号到达的时间、信号到达的时间差、信号到达角度来进行具体的测距,然后通过距离交会的方式确定待测点的位置。临近法的基本原理是将许多个带有特定位置信息的标记提前安置在需要定位的场地中,当用户进入某标记的信号范围内时,即可将此标记的位置作为用户所处的当前位置。行人航迹推算法的基本原理是已知用户确定的初始位置,然后用户携带传感装置如陀螺仪等在室内进行移动,通过其传感装置不断获取用户在室内移动的方向、速度,再利用数学公式计算出用户的位移,最终推导出用户在室内的运动轨迹。指纹定位法的基本过程较为复杂,一般分为两个阶段:离线阶段和在线阶段。离线阶段需要实验人员提前确定待测场地并对其进行划分,以便均匀的采集若干个含有指纹信息的已知点坐标,指纹信息即是每个已知点特定的位置信息,然后将其储存起来建立数据库,并对数据库进行一系列处理。在线阶段时用户由移动终端获取实时的未知点位置信息并传输到经处理后的数据库,通过检索匹配获取数据库中与未知点指纹相似度最为接近的已知点,其对应的坐标即可认为是用户所处的未知点坐标。相比于其他定位方法,指纹定位法的精度更高,并且对硬件设备的要求也不高。
3 基于不同距离度量的WKNN算法
基于指纹定位法的算法通常有人工神经网络、支持向量机、KNN法[10]。K最近邻(K-Nearest Neighbor,KNN)算法是一种当前理论基础比较成熟的算法,也是监督学习方法中较为常见的一种,已经在各个学科领域得到广泛应用。相较于其他机器学习算法,KNN算法思路简单、条理明朗,容易实现和理解,同时预测效果较好。同样属于分类算法,在获取一个算法模型前逻辑回归需要预先对数据进行大量的预处理,即花费在训练上的时间较长,且最终得到一个较为复杂的模型。KNN算法并不同,它几乎没有花费时间用于数据库的训练。通常,可利用投票的方法来应对分类任务,即预测的结果就是这K个样本中票数最多的类别标记;同时还可以取这K个样本的实际输出的平均值作为预测结果。其计算公式为:
其中,i为样本数。
在室内定位中,由于室内物体的遮挡以及墙体反射等不确定因素,不可避免地存在着定位误差。研究表明基于指纹室内定位的KNN算法中,这种误差与距离有关:测试样本点与训练样本点之间的距离越大,误差就越大,反之误差越小。因此还可以将上述的投票法及平均法结合距离进行加权,对距离近的样本给予较大的权重,对距离远的样本给予较小的权重,即WKNN算法,其计算公式为:
其中,参数Li为两个样本单元间的距离。
KNN算法在训练阶段仅仅只是把样本数据进行保存,在收到测试样本以后才开始处理。它的主要算法过程为:
首先输入训练样本集及测试样本集。其次采用插值法或者拟合法对所建立的数据集降噪,剔除个别误差过大或者含有缺失的数据。然后进行K值的选择。在实验中可采用循环估计法来选择最合适的值,且注意取值不宜过大。同时实验中需要不断调整来确定最优K值。以下文列举的三种距离计算方式为例分别进行计算,由此获得测试样本点到每一个训练样本点的距离。最后将上述步骤中的距离计算结果进行排序,在训练样本集中选择前K个与测试样本点距离最近的样本,进行分类后判别分类效果是否有效。其算法流程如图1所示。
相似性度量一般用来对某两个事物之间的相近程度进行综合评价[11]。如果这两个事物之间有着明显的差异,那么它们之间的相似性度量就会很小,反之它们之间的相似性度量就会很大。相似性度量常常被应用于分类任务中,最为直观的方法就是计算两个样本之间的“距离”并以此作为评价相似性度量的标准。距离越近,那么两个样本越相近。相似性度量在现实生活中的应用也很广泛,比如在网上购物时,确定商品单元之间或者用户间的相似程度,就可以推测用户喜好的商品并向他们推广。在室内定位算法中,同样可以根据不同相似性度量,即不同距离计算方式进行对比分析。
本文主要基于三种距离度量函数,即欧氏距离、马氏距离与卡方距离,在给定的样本集中各向量之间的尺度差别较大时与WKNN算法结合,以此比较它们在指纹定位中所获得的结果。
3.1 欧氏距离度量
欧式距离定义于欧几里得空间中,是一种在各学科领域中常见的表示空间内两点或多点距离的方法。假定二维空间内存在两个向量A1(x1,y1),A2(x2,y2),它们之间的欧氏距离可表示为:
同理两个三维向量A1(x1,y1,z1),A2(x2,y2,z2)之间的欧氏距離可表示为:
n维欧几里得空间内的两个向量A1(x1,x2,…,xn),A2(y1,y2,…,yn)之间的欧氏距离可表示为:
3.2 马氏距离度量
马氏距离最初被应用于统计学领域,它实质上指两个样本数据集协方差之间的距离。假设有n个样本向量X={x1,x2,x3,…xn},则其中样本向量间的马氏距离可表示为:
其中,S-1为协方差矩阵的逆,μ为向量均值,T为转置。
而其中向量xi与xj之间的马氏距离可表示为:
由此可知,如果该协方差矩阵为单位矩阵,上式即化简为欧氏距离的计算公式。
3.3 卡方距离度量
卡方距离是由数理统计中的列联表独立性检验而衍生出的概念,卡方统计量是由列联表分析获得的,并由此来衡量两个变量之间的独立性[12]。卡方统计量越大说明变量之间的独立性越大,其差异也就越明显。设两个直方图统计量为M,N是非负且有界的,则这两个统计量之间的二次式距离为:
其中,R为直方图统计量所构造的相似度加权矩阵。
如果M,N两个协方差矩阵的逆为矩阵R,上式即化为马氏距离的计算公式,如果该矩阵为单位矩阵,上式即化为欧氏距离的计算公式。由此可得到二次卡方距离,该距离是由二次式距离与卡方距离进行结合,其计算公式为:
其中,n为规格化参数,当n=0时,上式即化简为二次式距离的计算公式,当n=1/2且R为单位矩阵时,上式即化简为卡方距离的计算公式,其形式为:
其中,χ为卡方距离。卡方距离公式为:
综上所述,欧氏距离应用广泛,原理较为简单,且马氏距离、二次式距离在满足一定条件下均可化简为欧氏距离,因此人们为了方便通常选择欧氏距离公式进行距离计算,但欧氏距离仍存在不足之处:大部分情况下样本单元的不同特性之间存在着差别,比如在进行坐标点采集时,由于仪器、人为等因素采集到的坐标值存在着误差波动,在利用坐标表示距离测量值时欧氏距离会忽略掉这些差别,导致计算精度并不能很好地满足实验要求。马氏距离与欧氏距离不同:马氏距离有着独立的测量尺度,并在进行计算时考虑到了样本单元存在着特性间的相互联系,且这些联系与物理量的基本属性无关,即两个样本单位之间的马氏距离与原始数据的测量单位无关。它能更有效地用来计算两个未知样本之间的相似度。欧氏距离、马氏距离均表示样本单元之间的绝对距离,在WKNN算法中可利用相对距离在不同样本特征量间赋予不同权重,这种衡量更能体现分类任务的实际意义[13]。卡方距离能有效地反映各个样本单元不同特性间的相对距离的变化。同时以上三种距离度量均可应用于WKNN算法中,并由此对指纹定位的效果进行比较。
4 实验与结果分析
为了验证本文的理论基础,将实验场所选在了本校学院楼负一楼实验室。实验室长10 m,宽9 m,以1.5 m×1.5 m的尺寸将其均匀划分为40个网格区域。以实验室视图左下角为原点,右方向为X轴,上方向为Y轴建立坐标系。在每个网格顶点处均布置样本指纹点,并基于原点及网格尺寸建立坐标,此坐标可作为每个点的真实坐标。选择同一型号的4个AP设备分别放置在实验室角落,其型号为TP-LINK TL-WDR5620 AC1200,为保证实验的准确性,实验室内仅放有木制书柜及办公桌,并无金属障碍物,实验室布局图如图2所示。
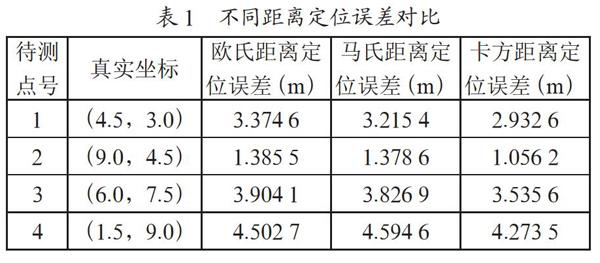
离线阶段,移动终端采用同一型号手机采集每个样本点的RSS。每个样本点的采样间隔为6 s,每个点平均采集10次,将采集到的RSS取平均值输入到数据库中。在线阶段,在实验室空旷地带随机选择25个网格顶点作为测试点,点位RSS采集方式与样本点一致。将测试点的坐标作为实验室定位坐标,以真实坐标与定位坐标之间的距离作为坐标误差,取部分点展示实验结果如表1所示。
最终的实验结果为,采用欧式距离得到的平均定位误差为4.165 7 m,采用马氏距离得到的平均定位误差为4.097 6 m,采用卡方距离得到的平均定位误差为3.835 6 m。如图3所示,当定位误差在2 m以内时,马氏距离与欧氏距离的误差累计分布相当,卡方距离明显有着更高的误差累积分布,定位误差在2 m~6 m时,马氏距离的误差累积分布略高于欧氏距离。虽然定位误差在6 m以上时卡方距离的误差累积分布仍是最高,但卡方距离的最大距离误差为8.2360 m,低于马氏距离和欧氏距离的最大距离误差,且误差波动较小。因此,基于卡方距离度量的指纹定位有着更高的定位精度且本文验证了不同RSS向量中存在特征向量间的差别。
5 结 论
本文基于传统欧式距离度量的WKNN算法,分别利用马氏距离、卡方距离进行对比,并应用到指纹室内定位中做出比较。通常情况下,每个坐标点的贡献相对于欧氏距离是相同的,因此很难克服各个分量之间性质的差别。马氏距离可以排除这些干扰,但同时会将协方差阵存在的微小不稳定性放大化。卡方距离在不同样本特征量间赋予不同权重,使总体变异带来的影响得到缓冲,有效地降低了实验过程中的误差累积。试验结果表明,卡方距离定位精度明显更高,更有利于替代欧氏距离作为相似度度量。本文提出的基于卡方距离的WKNN算法可为之后的室内定位研究提供参考。
参考文献:
[1] 邓中亮,尹露,唐诗浩,等.室内定位关键技术综述 [J].导航定位与授时,2018(3):14-23.
[2] 裴凌,刘东辉,钱久超.室内定位技术与应用综述 [J].导航定位与授时,2017,4(3):1-10.
[3] 李博心,祁浩然,鲁祥,等.室内定位算法与技术综述 [J].电子元器件与信息技术,2020,4(1):47-50.
[4] YOUSSEF M. Horus:A WLAN-based Indoor Location DeterminationSystem [D].Alexandria:Alexandria University,2004.
[5] 王培良,张婷,肖英杰.改进指纹库精度下的室内定位算法研究 [J].电子技术应用,2018,44(10):97-101+105.
[6] 倪巍,王宗欣.基于接收信号强度测量的室内定位算法 [J].复旦学报(自然科学版),2004(1):72-76.
[7] 孙瑜,范平志.射频识别技术及其在室内定位中的应用 [J].计算机应用,2005(5):1205-1208.
[8] NIU J W,WANG B W,SHU L,et al. ZIL:An Energy-Efficient Indoor Localization System Using ZigBee Radio to Detect WiFi Fingerprints [J].IEEE Journal on Selected Areas in Communications,2015,33(7):1431-1442.
[9] 王星星,叢思安.室内定位研究方法综述 [J].软件导刊,2019,18(9):9-12.
[10] 厚丹妮.基于深度学习的位置指纹室内定位算法研究 [D].西安:西安电子科技大学,2019.
[11] 丁义,杨建.欧式距离与标准化欧式距离在k近邻算法中的比较 [J].软件,2020,41(10):135-136+140.
[12] 陶峥,王洪玉.基于卡方距离改进的WLAN室内定位算法 [J].计算机技术与发展,2016,26(9):50-55.
[13] 谢红,赵洪野.基于卡方距离度量的改进KNN算法 [J].应用科技,2015,42(1):10-14.
作者简介:韩雨辰(1996—),男,汉族,安徽阜阳人,硕士在读,研究方向:室内定位。

